1 results
Global existence of the strong solution to the 3D incompressible micropolar equations with fractional partial dissipation
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 13 September 2022, pp. 1516-1539
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
-
In this paper, we considered the global strong solution to the 3D incompressible micropolar equations with fractional partial dissipation. Whether or not the classical solution to the 3D Navier–Stokes equations can develop finite-time singularity remains an outstanding open problem, so does the same issue on the 3D incompressible micropolar equations. We establish the global-in-time existence and uniqueness strong solutions to the 3D incompressible micropolar equations with fractional partial velocity dissipation and microrotation diffusion with the initial data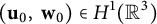
$(\mathbf {u}_0,\ \mathbf {w}_0)\in H^1(\mathbb {R}^3)$.
