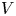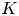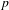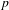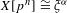Refine search
Actions for selected content:
7 results
1 - Finite group schemes
-
-
- Book:
- Groups St Andrews 2022 in Newcastle
- Published online:
- 21 November 2024
- Print publication:
- 12 December 2024, pp 1-52
-
- Chapter
- Export citation
IV - Composition algebras
-
- Book:
- Albert Algebras over Commutative Rings
- Published online:
- 07 November 2024
- Print publication:
- 21 November 2024, pp 123-251
-
- Chapter
- Export citation
IX - Group schemes
-
- Book:
- Albert Algebras over Commutative Rings
- Published online:
- 07 November 2024
- Print publication:
- 21 November 2024, pp 567-619
-
- Chapter
- Export citation
The Grothendieck–Serre conjecture over valuation rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 317-355
- Print publication:
- February 2024
-
- Article
- Export citation
THE DISTRIBUTION OF TORSION SUBSCHEMES OF ABELIAN VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 15 December 2014, pp. 693-710
- Print publication:
- October 2016
-
- Article
- Export citation
Finite Flat Group Schemes over Local Artin Rings
-
- Journal:
- Compositio Mathematica / Volume 128 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1-15
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
Finite Group Schemes over Bases with Low Ramification
-
- Journal:
- Compositio Mathematica / Volume 119 / Issue 3 / December 1999
- Published online by Cambridge University Press:
- 04 December 2007, pp. 239-320
- Print publication:
- December 1999
-
- Article
-
- You have access
- Export citation