Article contents
The Grothendieck–Serre conjecture over valuation rings
Published online by Cambridge University Press: 05 January 2024
Abstract
In this article, we establish the Grothendieck–Serre conjecture over valuation rings: for a reductive group scheme 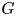 $G$ over a valuation ring
$G$ over a valuation ring 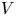 $V$ with fraction field
$V$ with fraction field 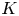 $K$, a
$K$, a 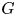 $G$-torsor over
$G$-torsor over 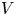 $V$ is trivial if it is trivial over
$V$ is trivial if it is trivial over 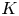 $K$. This result is predicted by the original Grothendieck–Serre conjecture and the resolution of singularities. The novelty of our proof lies in overcoming subtleties brought by general nondiscrete valuation rings. By using flasque resolutions and inducting with local cohomology, we prove a non-Noetherian counterpart of Colliot-Thélène–Sansuc's case of tori. Then, taking advantage of techniques in algebraization, we obtain the passage to the Henselian rank-one case. Finally, we induct on Levi subgroups and use the integrality of rational points of anisotropic groups to reduce to the semisimple anisotropic case, in which we appeal to properties of parahoric subgroups in Bruhat–Tits theory to conclude. In the last section, by using extension properties of reflexive sheaves on formal power series over valuation rings and patching of torsors, we prove a variant of Nisnevich's purity conjecture.
$K$. This result is predicted by the original Grothendieck–Serre conjecture and the resolution of singularities. The novelty of our proof lies in overcoming subtleties brought by general nondiscrete valuation rings. By using flasque resolutions and inducting with local cohomology, we prove a non-Noetherian counterpart of Colliot-Thélène–Sansuc's case of tori. Then, taking advantage of techniques in algebraization, we obtain the passage to the Henselian rank-one case. Finally, we induct on Levi subgroups and use the integrality of rational points of anisotropic groups to reduce to the semisimple anisotropic case, in which we appeal to properties of parahoric subgroups in Bruhat–Tits theory to conclude. In the last section, by using extension properties of reflexive sheaves on formal power series over valuation rings and patching of torsors, we prove a variant of Nisnevich's purity conjecture.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
- 1
- Cited by


