The tidal flow through a channel connecting two basins with different tidal regimes can be optimally controlled by means of a turbine fence or array to maximise the extracted mechanical power. The paper gives the optimal control strategy as a function of the blockage ratio 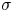 $\sigma$, i.e. the ratio of the turbine cross-section to the cross-section of the local passage of a turbine. The results presented are a physically consistent generalisation of the results of Garrett & Cummins (Proc. R. Soc. Lond. A, vol. 461, 2060, pp, 2563–2572), valid only for
$\sigma$, i.e. the ratio of the turbine cross-section to the cross-section of the local passage of a turbine. The results presented are a physically consistent generalisation of the results of Garrett & Cummins (Proc. R. Soc. Lond. A, vol. 461, 2060, pp, 2563–2572), valid only for 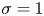 $\sigma =1$ and turbine efficiency of one, now for arbitrary blockage ratio
$\sigma =1$ and turbine efficiency of one, now for arbitrary blockage ratio 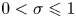 $0 < \sigma \leqslant 1$. Published research over the past decade on the same topic has taken the momentum equation and the turbine drag force as a starting point. The new approach presented here, in contrast, takes the energy equation as the starting point and uses the relative volume flow as the control variable. As the work shows, this new approach has three advantages. First, starting with the energy equation allows us to derive an optimal flow control problem resulting in an Euler–Lagrange equation using the physically consistent and experimentally validated actuator disk model for the free surface flow of Pelz et al. (J. Fluid Mech., vol. 889, 2020) in a direct and formal way. The optimal control problem is solved (a) numerically and (b) analytically. In the latter case, the turbine characteristics are approximated by a rational function in the relevant design and operating range. The analytical solution (b) validated against the numerical solution (a) is surprisingly concise and easy to apply in practice, as shown by use cases. Second, instead of the induction factor, we use the volume flow that is the same for all turbines in a cascade, i.e. a row of turbines in the direction of flow, which significantly reduces the complexity of the optimal control task of turbine arrays. Third, we obtain a well-founded energy estimate, whereas previous methods overestimate the energy yield due to inconsistent turbine disc models (for the consistency and valid parameter ranges of different models, also in comparison with experiments, see Pelz et al., J. Fluid Mech., vol. 889, 2020). The results can be used for the conceptual design of turbine arrays, but also for a sound physically realistic and consistent resource assessment of tidal power for a system consisting of two basins, a channel and a turbine fence with
$0 < \sigma \leqslant 1$. Published research over the past decade on the same topic has taken the momentum equation and the turbine drag force as a starting point. The new approach presented here, in contrast, takes the energy equation as the starting point and uses the relative volume flow as the control variable. As the work shows, this new approach has three advantages. First, starting with the energy equation allows us to derive an optimal flow control problem resulting in an Euler–Lagrange equation using the physically consistent and experimentally validated actuator disk model for the free surface flow of Pelz et al. (J. Fluid Mech., vol. 889, 2020) in a direct and formal way. The optimal control problem is solved (a) numerically and (b) analytically. In the latter case, the turbine characteristics are approximated by a rational function in the relevant design and operating range. The analytical solution (b) validated against the numerical solution (a) is surprisingly concise and easy to apply in practice, as shown by use cases. Second, instead of the induction factor, we use the volume flow that is the same for all turbines in a cascade, i.e. a row of turbines in the direction of flow, which significantly reduces the complexity of the optimal control task of turbine arrays. Third, we obtain a well-founded energy estimate, whereas previous methods overestimate the energy yield due to inconsistent turbine disc models (for the consistency and valid parameter ranges of different models, also in comparison with experiments, see Pelz et al., J. Fluid Mech., vol. 889, 2020). The results can be used for the conceptual design of turbine arrays, but also for a sound physically realistic and consistent resource assessment of tidal power for a system consisting of two basins, a channel and a turbine fence with 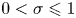 $0<\sigma \leqslant 1$ and operated in a complete tidal cycle.
$0<\sigma \leqslant 1$ and operated in a complete tidal cycle.
