We present a quantitative isolation property of the lifts of properly immersed geodesic planes in the frame bundle of a geometrically finite hyperbolic $3$-manifold. Our estimates are polynomials in the tight areas and Bowen–Margulis–Sullivan densities of geodesic planes, with degree given by the modified critical exponents.

We construct some cusped finite-volume hyperbolic n-manifolds 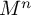$M^n$ that fibre algebraically in all the dimensions 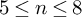$5\leq n \leq 8$. That is, there is a surjective homomorphism 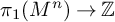$\pi _1(M^n) \to {\mathbb {Z}}$ with finitely generated kernel. The kernel is also finitely presented in the dimensions 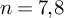$n=7, 8$, and this leads to the first examples of hyperbolic n-manifolds 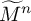$\widetilde M^n$ whose fundamental group is finitely presented but not of finite type. These n-manifolds 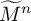$\widetilde M^n$ have infinitely many cusps of maximal rank and, hence, infinite Betti number 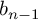$b_{n-1}$. They cover the finite-volume manifold 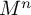$M^n$. We obtain these examples by assigning some appropriate colours and states to a family of right-angled hyperbolic polytopes $P^5, \ldots , P^8$, and then applying some arguments of Jankiewicz, Norin and Wise [18] and Bestvina and Brady [7]. We exploit in an essential way the remarkable properties of the Gosset polytopes dual to 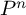$P^n$, and the algebra of integral octonions for the crucial dimensions 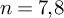$n=7,8$.