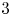1. Introduction
Let ![]() $\mathbb {H}^3$ denote the hyperbolic
$\mathbb {H}^3$ denote the hyperbolic ![]() $3$-space, and let
$3$-space, and let ![]() $G:=\operatorname {PSL}_2(\mathbb {C})$, which can be identified with the group
$G:=\operatorname {PSL}_2(\mathbb {C})$, which can be identified with the group ![]() $\operatorname {Isom}^+(\mathbb {H}^3)$ of all orientation preserving isometries of
$\operatorname {Isom}^+(\mathbb {H}^3)$ of all orientation preserving isometries of ![]() $\mathbb {H}^3$. Any complete orientable hyperbolic
$\mathbb {H}^3$. Any complete orientable hyperbolic ![]() $3$-manifold can be presented as a quotient
$3$-manifold can be presented as a quotient ![]() $M=\Gamma \backslash \mathbb {H}^3$ where
$M=\Gamma \backslash \mathbb {H}^3$ where ![]() $\Gamma$ is a torsion-free discrete subgroup of
$\Gamma$ is a torsion-free discrete subgroup of ![]() $G$. An oriented geodesic plane in
$G$. An oriented geodesic plane in ![]() $M$ is the image of a totally geodesic immersion of the hyperbolic plane
$M$ is the image of a totally geodesic immersion of the hyperbolic plane ![]() $\mathbb {H}^2\subset \mathbb {H}^3$ equipped with an orientation under the quotient map
$\mathbb {H}^2\subset \mathbb {H}^3$ equipped with an orientation under the quotient map ![]() $\mathbb {H}^3\to \Gamma \backslash \mathbb {H}^3$. In this paper, all geodesic planes are assumed to be oriented. Set
$\mathbb {H}^3\to \Gamma \backslash \mathbb {H}^3$. In this paper, all geodesic planes are assumed to be oriented. Set ![]() $X:=\Gamma \backslash G$. Via the identification of
$X:=\Gamma \backslash G$. Via the identification of ![]() $X$ with the oriented frame bundle
$X$ with the oriented frame bundle ![]() $\operatorname {F}\! {{M}}$, a geodesic plane in
$\operatorname {F}\! {{M}}$, a geodesic plane in ![]() $M$ arises as the image of a unique
$M$ arises as the image of a unique ![]() $\operatorname {PSL}_2(\mathbb {R})$-orbit under the base point projection map
$\operatorname {PSL}_2(\mathbb {R})$-orbit under the base point projection map
Moreover, a properly immersed geodesic plane in ![]() $M$ corresponds to a closed
$M$ corresponds to a closed ![]() $\operatorname {PSL}_2(\mathbb {R})$-orbit in
$\operatorname {PSL}_2(\mathbb {R})$-orbit in ![]() $X$.
$X$.
Setting ![]() $H:=\operatorname {PSL}_2(\mathbb {R})$, the main goal of this paper is to obtain a quantitative isolation result for closed
$H:=\operatorname {PSL}_2(\mathbb {R})$, the main goal of this paper is to obtain a quantitative isolation result for closed ![]() $H$-orbits in
$H$-orbits in ![]() $X$ when
$X$ when ![]() $\Gamma$ is a geometrically finite group. Fix a left invariant Riemannian metric on
$\Gamma$ is a geometrically finite group. Fix a left invariant Riemannian metric on ![]() $G$, which projects to the hyperbolic metric on
$G$, which projects to the hyperbolic metric on ![]() $\mathbb {H}^3$. This induces the distance
$\mathbb {H}^3$. This induces the distance ![]() $d$ on
$d$ on ![]() $X$ so that the canonical projection
$X$ so that the canonical projection ![]() $G\to X$ is a local isometry. We use this Riemannian structure on
$G\to X$ is a local isometry. We use this Riemannian structure on ![]() $G$ to define the volume of a closed
$G$ to define the volume of a closed ![]() $H$-orbit in
$H$-orbit in ![]() $X$. For a closed subset
$X$. For a closed subset ![]() $S\subset X$ and
$S\subset X$ and ![]() ${\varepsilon }>0$,
${\varepsilon }>0$, ![]() $B(S, {\varepsilon })$ denotes the
$B(S, {\varepsilon })$ denotes the ![]() ${\varepsilon }$-neighborhood of
${\varepsilon }$-neighborhood of ![]() $S$.
$S$.
The case when  $M$ is compact
$M$ is compact
We first state the result for compact hyperbolic ![]() $3$-manifolds. In this case, Ratner [Reference RatnerRat91] and Shah [Reference ShahSha91] independently showed that every
$3$-manifolds. In this case, Ratner [Reference RatnerRat91] and Shah [Reference ShahSha91] independently showed that every ![]() $H$-orbit is either compact or dense in
$H$-orbit is either compact or dense in ![]() $X$. Moreover, there are only countably many compact
$X$. Moreover, there are only countably many compact ![]() $H$-orbits in
$H$-orbits in ![]() $X$. Mozes and Shah [Reference Mozes and ShahMS95] proved that an infinite sequence of compact
$X$. Mozes and Shah [Reference Mozes and ShahMS95] proved that an infinite sequence of compact ![]() $H$-orbits becomes equidistributed in
$H$-orbits becomes equidistributed in ![]() $X$. Our questions concern the following quantitative isolation property: for given compact
$X$. Our questions concern the following quantitative isolation property: for given compact ![]() $H$-orbits
$H$-orbits ![]() $Y\!$ and
$Y\!$ and ![]() $Z$ in
$Z$ in ![]() $X$,
$X$,
(1) How close can
 $Y$ approach
$Y$ approach  $Z$?
$Z$?(2) Given
 ${\varepsilon }>0$, what portion of
${\varepsilon }>0$, what portion of  $Y\!$ enters into the
$Y\!$ enters into the  $\varepsilon$-neighborhood of
$\varepsilon$-neighborhood of  $Z$?
$Z$?
It turns out that volumes of compact orbits are the only complexity which measures their quantitative isolation property. The following theorem was proved by Margulis in an unpublished note.
Theorem 1.1 (Margulis)
Let ![]() $\Gamma$ be a cocompact lattice in
$\Gamma$ be a cocompact lattice in ![]() $G$. For every
$G$. For every ![]() $1/3\le s<1$, the following hold for any compact
$1/3\le s<1$, the following hold for any compact ![]() $H$-orbits
$H$-orbits ![]() $Y\ne Z$ in
$Y\ne Z$ in ![]() $X$.
$X$.
(1) We have
where \[ d(Y,Z )\gg \alpha_s^{-4/s} \cdot \operatorname{Vol}(Y)^{-1/s} \operatorname{Vol}(Z)^{-1/s} \]
\[ d(Y,Z )\gg \alpha_s^{-4/s} \cdot \operatorname{Vol}(Y)^{-1/s} \operatorname{Vol}(Z)^{-1/s} \]
 $\alpha _s= ({1}/({1-s}))^{1/(1-s)}$.
$\alpha _s= ({1}/({1-s}))^{1/(1-s)}$.(2) For all
 $0<\varepsilon < 1$,
where
$0<\varepsilon < 1$,
where \[ m_{Y}(Y\cap B(Z, \varepsilon)) \ll \alpha_s^4 \cdot \varepsilon^{s} \cdot \operatorname{Vol}(Z) \]
\[ m_{Y}(Y\cap B(Z, \varepsilon)) \ll \alpha_s^4 \cdot \varepsilon^{s} \cdot \operatorname{Vol}(Z) \]
 $m_Y$ denotes the
$m_Y$ denotes the  $H$-invariant probability measure on
$H$-invariant probability measure on  $Y$.
$Y$.
In both statements, the implied constants depend only on the injectivity radius of ![]() $\Gamma \backslash G$ (see (A.9) and (A.10) for more details).
$\Gamma \backslash G$ (see (A.9) and (A.10) for more details).
Remark 1.2 (1) By recent work [Reference Margulis and MohammadiMM22, Reference Bader, Fisher, Miller and StoverBFMS21], there may be infinitely many compact ![]() $H$-orbits only when
$H$-orbits only when ![]() $\Gamma$ is an arithmetic lattice.
$\Gamma$ is an arithmetic lattice.
(2) Theorem 1.1 for some exponent ![]() $s$ is proved in [Reference Einsiedler, Margulis and VenkateshEMV09, Lemma 10.3]. The proof in [Reference Einsiedler, Margulis and VenkateshEMV09] is based on the effective ergodic theorem which relies on the arithmeticity of
$s$ is proved in [Reference Einsiedler, Margulis and VenkateshEMV09, Lemma 10.3]. The proof in [Reference Einsiedler, Margulis and VenkateshEMV09] is based on the effective ergodic theorem which relies on the arithmeticity of ![]() $\Gamma$ via uniform spectral gap on compact
$\Gamma$ via uniform spectral gap on compact ![]() $H$-orbits; the exponent
$H$-orbits; the exponent ![]() $s$ obtained in their approach however is much smaller than
$s$ obtained in their approach however is much smaller than ![]() $1$.
$1$.
(3) Margulis’ proof does not rely on the arithmeticity of ![]() $\Gamma$ and is based on the construction of a certain function on
$\Gamma$ and is based on the construction of a certain function on ![]() $Y$ which measures the distance
$Y$ which measures the distance ![]() $d(y, Z)$ for
$d(y, Z)$ for ![]() $y\in Y$ (cf. (1.14)). A similar function appeared first in the work of Eskin, Mozes and Margulis in the study of a quantitative version of the Oppenheim conjecture [Reference Eskin, Margulis and MozesEMM98], and later in several other works (e.g. [Reference Eskin and MargulisEM04, Reference Benoist and QuintBQ12, Reference Eskin, Mirzakhani and MohammadiEMM15]).
$y\in Y$ (cf. (1.14)). A similar function appeared first in the work of Eskin, Mozes and Margulis in the study of a quantitative version of the Oppenheim conjecture [Reference Eskin, Margulis and MozesEMM98], and later in several other works (e.g. [Reference Eskin and MargulisEM04, Reference Benoist and QuintBQ12, Reference Eskin, Mirzakhani and MohammadiEMM15]).
General geometrically finite case
We now consider a general hyperbolic ![]() $3$-manifold
$3$-manifold ![]() ${M}=\Gamma \backslash \mathbb {H}^3$. Denote by
${M}=\Gamma \backslash \mathbb {H}^3$. Denote by ![]() $\Lambda \subset \partial \mathbb {H}^3$ the limit set of
$\Lambda \subset \partial \mathbb {H}^3$ the limit set of ![]() $\Gamma$ and by
$\Gamma$ and by ![]() ${\operatorname {core}}\, M$ the convex core of
${\operatorname {core}}\, M$ the convex core of ![]() $M$, i.e.
$M$, i.e.
where ![]() $\operatorname {hull} \Lambda \subset \mathbb {H}^3$ denotes the convex hull of
$\operatorname {hull} \Lambda \subset \mathbb {H}^3$ denotes the convex hull of ![]() $\Lambda$. In the rest of the introduction, we assume that
$\Lambda$. In the rest of the introduction, we assume that ![]() $M$ is geometrically finite, that is, the unit neighborhood of
$M$ is geometrically finite, that is, the unit neighborhood of ![]() ${\operatorname {core}}\, M$ has finite volume.
${\operatorname {core}}\, M$ has finite volume.
Let ![]() $Y\subset X$ be a closed
$Y\subset X$ be a closed ![]() $H$-orbit and
$H$-orbit and ![]() $S_Y=\Delta _Y\backslash \mathbb {H}^2$ be the associated hyperbolic surface, where
$S_Y=\Delta _Y\backslash \mathbb {H}^2$ be the associated hyperbolic surface, where ![]() $\Delta _Y< H$ is the stabilizer in
$\Delta _Y< H$ is the stabilizer in ![]() $H$ of a point in
$H$ of a point in ![]() $Y$. We assume that
$Y$. We assume that ![]() $Y$ is non-elementary, that is,
$Y$ is non-elementary, that is, ![]() $\Delta _Y$ is not virtually cyclic; otherwise, we cannot expect an isolation phenomenon for
$\Delta _Y$ is not virtually cyclic; otherwise, we cannot expect an isolation phenomenon for ![]() $Y$, as there is a continuous family of parallel elementary closed
$Y$, as there is a continuous family of parallel elementary closed ![]() $H$-orbits in general when
$H$-orbits in general when ![]() $M$ is of infinite volume. It is known that
$M$ is of infinite volume. It is known that ![]() $S_Y$ is always geometrically finite [Reference Oh and ShahOS13, Theorem 4.7].
$S_Y$ is always geometrically finite [Reference Oh and ShahOS13, Theorem 4.7].
Let ![]() $0<\delta (Y)\le 1$ denote the critical exponent of
$0<\delta (Y)\le 1$ denote the critical exponent of ![]() $S_Y$, i.e. the abscissa of the convergence of the series
$S_Y$, i.e. the abscissa of the convergence of the series ![]() $\sum _{\gamma \in \Delta _Y} e^{-s d(o, \gamma (o))}$ for some
$\sum _{\gamma \in \Delta _Y} e^{-s d(o, \gamma (o))}$ for some ![]() $o\in \mathbb {H}^2$. We define the following modified critical exponent of
$o\in \mathbb {H}^2$. We define the following modified critical exponent of ![]() $Y$:
$Y$:
 \begin{equation} \delta_Y:=\begin{cases} \delta(Y) & \text{if $S_Y$ has no cusp,}\\ 2\delta(Y)-1 & \text{otherwise;}\end{cases} \end{equation}
\begin{equation} \delta_Y:=\begin{cases} \delta(Y) & \text{if $S_Y$ has no cusp,}\\ 2\delta(Y)-1 & \text{otherwise;}\end{cases} \end{equation}
note that ![]() $0<\delta _Y\le \delta (Y) \le 1$, and
$0<\delta _Y\le \delta (Y) \le 1$, and ![]() $\delta _Y=1$ if and only if
$\delta _Y=1$ if and only if ![]() $S_Y$ has finite area.
$S_Y$ has finite area.
In generalizing Theorem 1.1(1), we first observe that the distance ![]() $d(Y, Z)$ between two closed
$d(Y, Z)$ between two closed ![]() $H$-orbits
$H$-orbits ![]() $Y, Z$ may be zero, e.g. if they both have cusps going into the same cuspidal end of
$Y, Z$ may be zero, e.g. if they both have cusps going into the same cuspidal end of ![]() $X$. To remedy this issue, we use the thick–thin decomposition of
$X$. To remedy this issue, we use the thick–thin decomposition of ![]() ${\operatorname {core}}\, M$. For
${\operatorname {core}}\, M$. For ![]() $p\in M$, we denote by
$p\in M$, we denote by ![]() $\operatorname {inj} p$ the injectivity radius at
$\operatorname {inj} p$ the injectivity radius at ![]() $p$. For all
$p$. For all ![]() ${\varepsilon }>0$, the
${\varepsilon }>0$, the ![]() ${\varepsilon }$-thick part
${\varepsilon }$-thick part
is compact, and for all sufficiently small ![]() ${\varepsilon }>0$, the
${\varepsilon }>0$, the ![]() ${\varepsilon }$-thin part given by
${\varepsilon }$-thin part given by ![]() ${\operatorname {core}}\, M-({\operatorname {core}}\, M)_{{\varepsilon }}$ is contained in finitely many disjoint cuspidal ends, i.e. images of horoballs in
${\operatorname {core}}\, M-({\operatorname {core}}\, M)_{{\varepsilon }}$ is contained in finitely many disjoint cuspidal ends, i.e. images of horoballs in ![]() $\Gamma \backslash \mathbb {H}^3$. Let
$\Gamma \backslash \mathbb {H}^3$. Let ![]() $X_0\subset X$ denote the renormalized frame bundle
$X_0\subset X$ denote the renormalized frame bundle ![]() $\operatorname {RF}\! {M}$ (see (2.1)). Using the fact that the projection of
$\operatorname {RF}\! {M}$ (see (2.1)). Using the fact that the projection of ![]() $X_0$ is contained in
$X_0$ is contained in ![]() ${\operatorname {core}}\, M$ under
${\operatorname {core}}\, M$ under ![]() $\pi$, we define the
$\pi$, we define the ![]() ${\varepsilon }$-thick part of
${\varepsilon }$-thick part of ![]() $X_0$ as follows:
$X_0$ as follows:
The following theorem extends Theorem 1.1 to all geometrically finite hyperbolic manifolds.
Theorem 1.5 Let ![]() ${M}$ be a geometrically finite hyperbolic
${M}$ be a geometrically finite hyperbolic ![]() $3$-manifold. Let
$3$-manifold. Let ![]() $Y\ne Z$ be non-elementary closed
$Y\ne Z$ be non-elementary closed ![]() $H$-orbits in
$H$-orbits in ![]() $X$, and denote by
$X$, and denote by ![]() $m_Y$ the probability Bowen–Margulis–Sullivan measure on
$m_Y$ the probability Bowen–Margulis–Sullivan measure on ![]() $Y$. For every
$Y$. For every ![]() ${\delta _Y}/3\le s<\delta _Y$ the following hold.
${\delta _Y}/3\le s<\delta _Y$ the following hold.
(1) For all
 $0<{\varepsilon } \ll 1$, we have
(1.6)where:
$0<{\varepsilon } \ll 1$, we have
(1.6)where: \begin{equation} d (Y\cap X_\varepsilon, Z)\gg \alpha_{Y,s}^{-\star/s} \cdot \bigg(\frac{v_{Y,{\varepsilon}}}{\operatorname{area}_t Z} \bigg)^{1/s} \end{equation}
\begin{equation} d (Y\cap X_\varepsilon, Z)\gg \alpha_{Y,s}^{-\star/s} \cdot \bigg(\frac{v_{Y,{\varepsilon}}}{\operatorname{area}_t Z} \bigg)^{1/s} \end{equation}•
 $v_{Y,{\varepsilon }}=\min _{y\in Y\cap X_{\varepsilon }} {m_Y (B_Y(y, {\varepsilon }))}$ where
$v_{Y,{\varepsilon }}=\min _{y\in Y\cap X_{\varepsilon }} {m_Y (B_Y(y, {\varepsilon }))}$ where  $B_Y(y, {\varepsilon })$ is the
$B_Y(y, {\varepsilon })$ is the  ${\varepsilon }$-ball around
${\varepsilon }$-ball around  $y$ in the induced metric on
$y$ in the induced metric on  $Y$;
$Y$;•
 $\operatorname {area}_t Z$ denotes the tight area of
$\operatorname {area}_t Z$ denotes the tight area of  $S_Z$ relative to
$S_Z$ relative to  $M$ (Definition 1.7);
$M$ (Definition 1.7);•
 $\alpha _{Y,s}:=\big ({{\mathsf {s}}_Y}/({ \delta _Y-s}\big )) ^{1/ (\delta _Y-s)}$ where
$\alpha _{Y,s}:=\big ({{\mathsf {s}}_Y}/({ \delta _Y-s}\big )) ^{1/ (\delta _Y-s)}$ where  $\mathsf {s}_Y\!$ is the shadow constant of
$\mathsf {s}_Y\!$ is the shadow constant of  $Y$ (Definition 1.8).
$Y$ (Definition 1.8).
(2) For all
 $0<{\varepsilon } \ll 1$,
$0<{\varepsilon } \ll 1$,
 \[ m_{Y}(Y\cap B(Z, {\varepsilon})) \ll \alpha_{Y,s}^\star \cdot {{\varepsilon}}^{s}\cdot \operatorname{area}_t Z. \]
\[ m_{Y}(Y\cap B(Z, {\varepsilon})) \ll \alpha_{Y,s}^\star \cdot {{\varepsilon}}^{s}\cdot \operatorname{area}_t Z. \]
In both statements, the implied constants and ![]() $\star$ depend only on
$\star$ depend only on ![]() $\Gamma$.
$\Gamma$.
Remark (1) We give a proof of a more general version of Theorem 1.5(1) where ![]() $Z$ is allowed to be equal to
$Z$ is allowed to be equal to ![]() $Y$ (see Corollary 10.5 for a precise statement).
$Y$ (see Corollary 10.5 for a precise statement).
(2) When ![]() $X$ has finite volume, we have
$X$ has finite volume, we have ![]() $\delta _Y=1$ and
$\delta _Y=1$ and ![]() $m_Y$ is
$m_Y$ is ![]() $H$-invariant so that
$H$-invariant so that ![]() $v_{Y, {\varepsilon }}\asymp {\varepsilon }^3 \operatorname {Vol} (Y)^{-1}$. Moreover, the tight area
$v_{Y, {\varepsilon }}\asymp {\varepsilon }^3 \operatorname {Vol} (Y)^{-1}$. Moreover, the tight area ![]() $\operatorname {area}_tZ$ and the shadow constant
$\operatorname {area}_tZ$ and the shadow constant ![]() $\mathsf {s}_Y$ are simply the usual area of
$\mathsf {s}_Y$ are simply the usual area of ![]() $S_Z$ and a fixed constant (in fact, the constant can be taken to be
$S_Z$ and a fixed constant (in fact, the constant can be taken to be ![]() $2$) respectively. Therefore Theorem 1.5 recovers Theorem 1.1. Moreover, the exponent
$2$) respectively. Therefore Theorem 1.5 recovers Theorem 1.1. Moreover, the exponent ![]() $\star$ depends only on
$\star$ depends only on ![]() $G$ as well; this follows since the proofs of Theorem 9.18 and theorems in § 10, of which Theorem 1.5 is a special case, show that
$G$ as well; this follows since the proofs of Theorem 9.18 and theorems in § 10, of which Theorem 1.5 is a special case, show that ![]() $\star$ depends only on
$\star$ depends only on ![]() $\mathsf {s}_Y$,
$\mathsf {s}_Y$, ![]() $\mathsf {p}_Y$ and
$\mathsf {p}_Y$ and ![]() $\delta _Y$, which are all absolute constants in the finite volume case.
$\delta _Y$, which are all absolute constants in the finite volume case.
We now give definitions of the tight area ![]() $\operatorname {area}_t Z$ and the shadow constant
$\operatorname {area}_t Z$ and the shadow constant ![]() $\mathsf {s}_Y$ for a general geometrically finite case; these are new geometric invariants introduced in this paper.
$\mathsf {s}_Y$ for a general geometrically finite case; these are new geometric invariants introduced in this paper.
Definition 1.7 (Tight area of  $S$)
$S$)
For a properly immersed geodesic plane ![]() $S$ of
$S$ of ![]() $M$, the tight-area of
$M$, the tight-area of ![]() $S$ relative to
$S$ relative to ![]() $M$ is given by
$M$ is given by
where ![]() $\mathcal{N}(\operatorname{core}\, M)=\{p\in M: d(p, q)\le \text {inj}(q)\text{ for some } q\in \operatorname{core}\, M\}$ is the tight neighborhood of
$\mathcal{N}(\operatorname{core}\, M)=\{p\in M: d(p, q)\le \text {inj}(q)\text{ for some } q\in \operatorname{core}\, M\}$ is the tight neighborhood of ![]() ${\operatorname {core}}\, M$.
${\operatorname {core}}\, M$.
We show that ![]() $\operatorname {area}_t(S)$ is finite in Theorem 3.3, by proving that
$\operatorname {area}_t(S)$ is finite in Theorem 3.3, by proving that ![]() $S\cap \mathcal { N}({\operatorname {core}}\, M)$ is contained in the union of a bounded neighborhood of
$S\cap \mathcal { N}({\operatorname {core}}\, M)$ is contained in the union of a bounded neighborhood of ![]() ${\operatorname {core}}\, (S)$ and finitely many cusp-like regions (see Figure 1). We remark that the area of the intersection
${\operatorname {core}}\, (S)$ and finitely many cusp-like regions (see Figure 1). We remark that the area of the intersection ![]() $S\cap B({\operatorname {core}}\, M, 1)$ is not finite in general.
$S\cap B({\operatorname {core}}\, M, 1)$ is not finite in general.
Definition 1.8 (Shadow constant of  $Y$)
$Y$)
For a closed ![]() $H$-orbit
$H$-orbit ![]() $Y$ in
$Y$ in ![]() $X$, let
$X$, let ![]() $\Lambda _Y\subset \partial \mathbb {H}^2$ denote the limit set of
$\Lambda _Y\subset \partial \mathbb {H}^2$ denote the limit set of ![]() $\Delta _Y$,
$\Delta _Y$, ![]() $\{\nu _{p}:p\in \mathbb {H}^2\}$ the Patterson–Sullivan density for
$\{\nu _{p}:p\in \mathbb {H}^2\}$ the Patterson–Sullivan density for ![]() $\Delta _Y$, and
$\Delta _Y$, and ![]() $B_p(\xi, {\varepsilon })$ the
$B_p(\xi, {\varepsilon })$ the ![]() ${\varepsilon }$-neighborhood of
${\varepsilon }$-neighborhood of ![]() $\xi \in \partial \mathbb {H}^2$ with respect to the Gromov metric at
$\xi \in \partial \mathbb {H}^2$ with respect to the Gromov metric at ![]() $p$. The shadow constant of
$p$. The shadow constant of ![]() $Y$ is defined as follows:
$Y$ is defined as follows:
where ![]() $[\xi, \Lambda _Y]$ is the union of all geodesics connecting
$[\xi, \Lambda _Y]$ is the union of all geodesics connecting ![]() $\xi$ to a point in
$\xi$ to a point in ![]() $\Lambda _Y$.
$\Lambda _Y$.
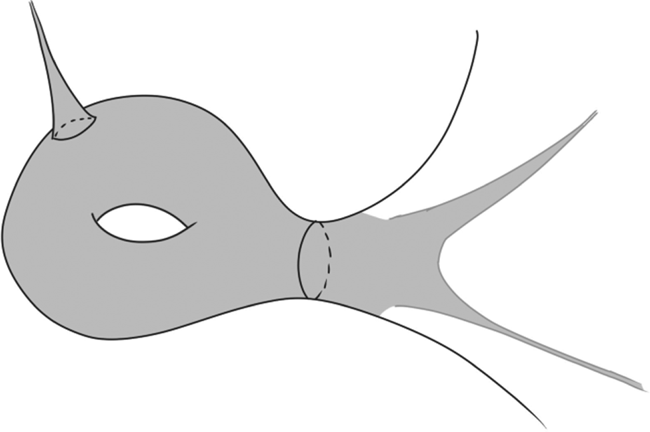
Figure 1. ![]() $S\cap \mathcal {N}({\operatorname {core}}\, M)$.
$S\cap \mathcal {N}({\operatorname {core}}\, M)$.
We show that ![]() $\mathsf {s}_Y<\infty$ in Theorem 4.8.
$\mathsf {s}_Y<\infty$ in Theorem 4.8.
Remark 1.10 If ![]() $Y$ is convex cocompact, then for all
$Y$ is convex cocompact, then for all ![]() $0<{\varepsilon }<1$, we have
$0<{\varepsilon }<1$, we have ![]() $v_{Y, {\varepsilon }}\asymp {\varepsilon }^{1+2\delta _Y}$ with the implied constant depending on
$v_{Y, {\varepsilon }}\asymp {\varepsilon }^{1+2\delta _Y}$ with the implied constant depending on ![]() $Y$. When
$Y$. When ![]() $Y$ has a cusp, Sullivan's shadow lemma (cf. Proposition 4.11) implies that
$Y$ has a cusp, Sullivan's shadow lemma (cf. Proposition 4.11) implies that ![]() $\lim _{{\varepsilon }\to 0} {\log v_{Y, {\varepsilon }}}/{\log {\varepsilon }}$ does not exist.
$\lim _{{\varepsilon }\to 0} {\log v_{Y, {\varepsilon }}}/{\log {\varepsilon }}$ does not exist.
A hyperbolic ![]() $3$-manifold
$3$-manifold ![]() ${M}$ is called convex cocompact acylindrical if
${M}$ is called convex cocompact acylindrical if ![]() ${\operatorname {core}}\, M$ is a compact manifold with no essential discs or cylinders which are not boundary parallel. For such a manifold, there exists a uniform positive lower bound for
${\operatorname {core}}\, M$ is a compact manifold with no essential discs or cylinders which are not boundary parallel. For such a manifold, there exists a uniform positive lower bound for ![]() $\delta (Y)=\delta _Y$ for all non-elementary closed
$\delta (Y)=\delta _Y$ for all non-elementary closed ![]() $H$-orbits
$H$-orbits ![]() $Y$ [Reference McMullen, Mohammadi and OhMMO17]; therefore the dependence of
$Y$ [Reference McMullen, Mohammadi and OhMMO17]; therefore the dependence of ![]() $\delta _Y$ can be removed in Theorem 1.5 if one is content with taking some
$\delta _Y$ can be removed in Theorem 1.5 if one is content with taking some ![]() $s$ which works uniformly for all such orbits.
$s$ which works uniformly for all such orbits.
Examples of ![]() $X$ with infinitely many closed
$X$ with infinitely many closed ![]() $H$-orbits are provided by the following theorem which can be deduced from [Reference McMullen, Mohammadi and OhMMO17, Reference McMullen, Mohammadi and OhMMO22, Reference Benoist and OhBO22].
$H$-orbits are provided by the following theorem which can be deduced from [Reference McMullen, Mohammadi and OhMMO17, Reference McMullen, Mohammadi and OhMMO22, Reference Benoist and OhBO22].
Theorem 1.11 Let ![]() ${M}_0$ be an arithmetic hyperbolic
${M}_0$ be an arithmetic hyperbolic ![]() $3$-manifold with a properly immersed geodesic plane. Any geometrically finite acylindrical hyperbolic
$3$-manifold with a properly immersed geodesic plane. Any geometrically finite acylindrical hyperbolic ![]() $3$-manifold
$3$-manifold ![]() ${M}$ which covers
${M}$ which covers ![]() ${M}_0$ contains infinitely many non-elementary properly immersed geodesic planes.
${M}_0$ contains infinitely many non-elementary properly immersed geodesic planes.
It is easy to construct examples of ![]() ${M}$ satisfying the hypothesis of this theorem. For instance, if
${M}$ satisfying the hypothesis of this theorem. For instance, if ![]() ${M}_0$ is an arithmetic hyperbolic
${M}_0$ is an arithmetic hyperbolic ![]() $3$-manifold with a properly embedded compact geodesic plane
$3$-manifold with a properly embedded compact geodesic plane ![]() $P$,
$P$, ![]() ${M}_0$ is covered by a geometrically finite acylindrical manifold
${M}_0$ is covered by a geometrically finite acylindrical manifold ![]() ${M}$ whose convex core has boundary isometric to
${M}$ whose convex core has boundary isometric to ![]() $P$.
$P$.
Finally, we mention the following application of Theorem 1.5 in view of recent interests in related counting problems [Reference Calegari, Marques and NevesCMN22].
Corollary 1.12 Let ![]() $\operatorname {Vol}(M)<\infty$, and let
$\operatorname {Vol}(M)<\infty$, and let ![]() $\mathcal {N}(T)$ denote the number of properly immersed totally geodesic planes
$\mathcal {N}(T)$ denote the number of properly immersed totally geodesic planes ![]() $P$ in
$P$ in ![]() $M$ of area at most
$M$ of area at most ![]() $T$. Then for any
$T$. Then for any ![]() $1/2< s<1$, we have
$1/2< s<1$, we have
see Corollary 10.7 for a detailed information on the dependence of the implied constant.
We remark that when ![]() $\operatorname {Vol} (M)<\infty$, the heuristics suggest
$\operatorname {Vol} (M)<\infty$, the heuristics suggest ![]() $s={\operatorname {dim} G/ H}=3$ in Theorem 1.5 and hence
$s={\operatorname {dim} G/ H}=3$ in Theorem 1.5 and hence ![]() $\mathcal {N}(T)\ll T$ in Corollary 1.12. Indeed, when
$\mathcal {N}(T)\ll T$ in Corollary 1.12. Indeed, when ![]() $\Gamma =\operatorname {PSL}_2 (\mathbb {Z}[i])$, the asymptotic
$\Gamma =\operatorname {PSL}_2 (\mathbb {Z}[i])$, the asymptotic ![]() $\mathcal {N}(T)\sim c \cdot T$, as suggested in [Reference SarnakSar05], has been obtained by Jung [Reference JungJun19] based on subtle number theoretic arguments.
$\mathcal {N}(T)\sim c \cdot T$, as suggested in [Reference SarnakSar05], has been obtained by Jung [Reference JungJun19] based on subtle number theoretic arguments.
Remark 1.13 We can also obtain an estimate for ![]() $\mathcal {N}(T)$ for a general geometrically finite hyperbolic manifold. By [Reference McMullen, Mohammadi and OhMMO17, Reference Benoist and OhBO22], if
$\mathcal {N}(T)$ for a general geometrically finite hyperbolic manifold. By [Reference McMullen, Mohammadi and OhMMO17, Reference Benoist and OhBO22], if ![]() $\operatorname {Vol} (M)=\infty$, there are only finitely many properly immersed geodesic planes of finite area (note that they are necessarily contained in the convex core of
$\operatorname {Vol} (M)=\infty$, there are only finitely many properly immersed geodesic planes of finite area (note that they are necessarily contained in the convex core of ![]() $M$); hence
$M$); hence ![]() $\sup _{T} \mathcal {N}(T) <\infty$. We also obtain that there exists
$\sup _{T} \mathcal {N}(T) <\infty$. We also obtain that there exists ![]() $N_0\ge 1$ (depending only on
$N_0\ge 1$ (depending only on ![]() $G$) such that for any
$G$) such that for any ![]() $1/2< s<1$, we have
$1/2< s<1$, we have
where the implied constant depends only on ![]() $s$ (see Remark 10.11 for details). Note that this kind of upper bound is meaningful despite the finiteness result mentioned above, as the implied constant is independent of
$s$ (see Remark 10.11 for details). Note that this kind of upper bound is meaningful despite the finiteness result mentioned above, as the implied constant is independent of ![]() $M$.
$M$.
Discussion on proofs
We discuss some of the main ingredients of the proof of Theorem 1.5. First consider the case when ![]() $X=\Gamma \backslash G$ is compact (the account below deviates slightly from Margulis’ original argument). Let
$X=\Gamma \backslash G$ is compact (the account below deviates slightly from Margulis’ original argument). Let ![]() ${\varepsilon }_X$ be the minimum injectivity radius of points in
${\varepsilon }_X$ be the minimum injectivity radius of points in ![]() $X$. The Lie algebra of
$X$. The Lie algebra of ![]() $G$ decomposes as
$G$ decomposes as ![]() $\mathfrak {sl}_2(\mathbb {R}) \oplus i\mathfrak {sl}_2(\mathbb {R})$. Hence, for each
$\mathfrak {sl}_2(\mathbb {R}) \oplus i\mathfrak {sl}_2(\mathbb {R})$. Hence, for each ![]() $y\in Y$, the set
$y\in Y$, the set
keeps track of all points of ![]() $Z\cap B(y, {\varepsilon }_X)$ in the direction transversal to
$Z\cap B(y, {\varepsilon }_X)$ in the direction transversal to ![]() $H$ (see Figure 2).
$H$ (see Figure 2).
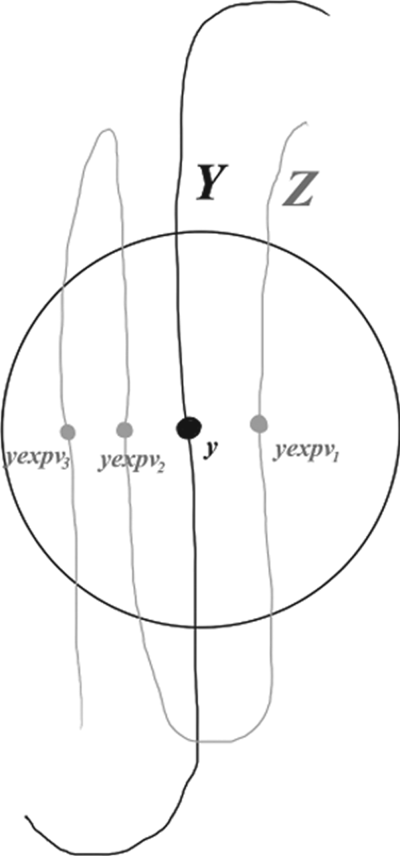
Figure 2. ![]() $I_Z(y)$.
$I_Z(y)$.
Therefore, the following function ![]() $f_s:Y\to [2,\infty )$ (
$f_s:Y\to [2,\infty )$ (![]() $0< s<1$) encodes the information on the distance
$0< s<1$) encodes the information on the distance ![]() $d(y, Z)$:
$d(y, Z)$:
 \begin{equation} f_s(y)=\begin{cases} \sum_{v\in I_Z(y)}\|v\|^{-s} & \text{if $I_Z(y)\neq\emptyset $},\\ {\varepsilon}_X^{-s} & \text{otherwise.} \end{cases} \end{equation}
\begin{equation} f_s(y)=\begin{cases} \sum_{v\in I_Z(y)}\|v\|^{-s} & \text{if $I_Z(y)\neq\emptyset $},\\ {\varepsilon}_X^{-s} & \text{otherwise.} \end{cases} \end{equation}A function of this type is referred to as a Margulis function in the literature.
The proof of Theorem 1.1 is based on the following fact: the average of ![]() $f_s$ is controlled by the volume of
$f_s$ is controlled by the volume of ![]() $Z$, i.e.
$Z$, i.e.
We prove the estimate in (1.15) using the following super-harmonicity type inequality: for any ![]() $1/3\le s<1$, there exist
$1/3\le s<1$, there exist ![]() $t=t_s>0$ and
$t=t_s>0$ and ![]() $b=b_s>1$ such that for all
$b=b_s>1$ such that for all ![]() $y\in Y$,
$y\in Y$,
where ![]() $({\mathsf {A}}_t f_s)(y)= \int _0^1 f_s(yu_ra_t)\,dr$,
$({\mathsf {A}}_t f_s)(y)= \int _0^1 f_s(yu_ra_t)\,dr$, ![]() $u_r=\bigl (\begin {smallmatrix} 1 & 0\\r & 1\end {smallmatrix}\bigr )$, and
$u_r=\bigl (\begin {smallmatrix} 1 & 0\\r & 1\end {smallmatrix}\bigr )$, and ![]() $a_t=\bigl (\begin {smallmatrix} e^{t/2} & 0\\0 & e^{-t/2}\end {smallmatrix}\bigr )$.
$a_t=\bigl (\begin {smallmatrix} e^{t/2} & 0\\0 & e^{-t/2}\end {smallmatrix}\bigr )$.
The proof of (1.16) is based on the inequality (A.1), which is essentially a lemma in linear algebra. We refer to Appendix A, where a more or less complete proof of Theorem 1.1 is given.
For a general geometrically finite hyperbolic manifold, many changes are required, and several technical difficulties arise. In general, there is no positive lower bound for the injectivity radius on ![]() $X$, and the shadow constant of
$X$, and the shadow constant of ![]() $Y$ appears in the linear algebra lemma (Lemma 5.6). These facts force us to incorporate the height of
$Y$ appears in the linear algebra lemma (Lemma 5.6). These facts force us to incorporate the height of ![]() $y$ as well as the shadow constant of
$y$ as well as the shadow constant of ![]() $Y$ in the definition of the Margulis function (see Definition 9.1). The correct substitutes for the volume measures on
$Y$ in the definition of the Margulis function (see Definition 9.1). The correct substitutes for the volume measures on ![]() $Y$ and
$Y$ and ![]() $Z$ turn out to be the Bowen–Margulis–Sullivan probability measure
$Z$ turn out to be the Bowen–Margulis–Sullivan probability measure ![]() $m_Y$ and the tight area of
$m_Y$ and the tight area of ![]() $Z$ respectively.
$Z$ respectively.
It is more common in the existing literature on the subject to define the operator ![]() ${\mathsf {A}}_t$ using averages over large spheres in
${\mathsf {A}}_t$ using averages over large spheres in ![]() $\mathbb {H}^2$. Our operator
$\mathbb {H}^2$. Our operator ![]() ${\mathsf {A}}_t$, however, is defined using averages over expanding horocyclic pieces; this choice is more amenable to the change of variables and iteration arguments for Patterson–Sullivan measures. Indeed, for a locally bounded Borel function
${\mathsf {A}}_t$, however, is defined using averages over expanding horocyclic pieces; this choice is more amenable to the change of variables and iteration arguments for Patterson–Sullivan measures. Indeed, for a locally bounded Borel function ![]() $f$ on
$f$ on ![]() $Y\cap X_0$ and for any
$Y\cap X_0$ and for any ![]() $y\in Y\cap X_0$,
$y\in Y\cap X_0$,
where ![]() $\mu _y$ is the Patterson–Sullivan measure on
$\mu _y$ is the Patterson–Sullivan measure on ![]() $yU$ (see (4.2)).
$yU$ (see (4.2)).
When ![]() $X$ is compact and hence
$X$ is compact and hence ![]() $m_Y$ is
$m_Y$ is ![]() $H$-invariant, (1.15) follows by simply integrating (1.16) with respect to
$H$-invariant, (1.15) follows by simply integrating (1.16) with respect to ![]() $m_Y$. In general, we resort to Lemma 7.3, the proof of which is based on an iterated version of (1.16) for
$m_Y$. In general, we resort to Lemma 7.3, the proof of which is based on an iterated version of (1.16) for ![]() ${\mathsf {A}}_{nt_0}$,
${\mathsf {A}}_{nt_0}$, ![]() $n\in \mathbb {N}$, for some
$n\in \mathbb {N}$, for some ![]() $t_0>0$, as well as on the fact that the Bowen–Margulis–Sullivan measure
$t_0>0$, as well as on the fact that the Bowen–Margulis–Sullivan measure ![]() $m_Y$ is
$m_Y$ is ![]() $a_{t_0}$-ergodic.
$a_{t_0}$-ergodic.
In fact, the main technical result of this paper can be summarized as follows.
Proposition 1.17 Let ![]() $\Gamma$ be a geometrically finite subgroup of
$\Gamma$ be a geometrically finite subgroup of ![]() $G$. Let
$G$. Let ![]() $Y\ne Z$ be non-elementary closed
$Y\ne Z$ be non-elementary closed ![]() $H$-orbits in
$H$-orbits in ![]() $X=\Gamma \backslash G$, and set
$X=\Gamma \backslash G$, and set ![]() $Y_0:=Y\cap X_0$. For any
$Y_0:=Y\cap X_0$. For any ![]() $ { \delta _Y}/{3} \le s<\delta _Y$, there exist
$ { \delta _Y}/{3} \le s<\delta _Y$, there exist ![]() $t_s>0$ and a locally bounded Borel function
$t_s>0$ and a locally bounded Borel function ![]() $F_s:Y_0\to (0, \infty )$ with the following properties.
$F_s:Y_0\to (0, \infty )$ with the following properties.
(1) For all
 $y\in Y_0$,
$y\in Y_0$,
 \[ d(y, Z) ^{-s}\le \mathsf{s}_Y^{\star} F_s(y). \]
\[ d(y, Z) ^{-s}\le \mathsf{s}_Y^{\star} F_s(y). \]
(2) For all
 $y\in Y_0$ and
$y\in Y_0$ and  $n\ge 1$,
$n\ge 1$,
 \[ \big({\mathsf{A}}_{nt_s} F_s\big) (y)\le \frac{1}{2^{n}} F_{s}(y)+ \alpha_{Y,s}^\star \operatorname{area}_t(S_Z). \]
\[ \big({\mathsf{A}}_{nt_s} F_s\big) (y)\le \frac{1}{2^{n}} F_{s}(y)+ \alpha_{Y,s}^\star \operatorname{area}_t(S_Z). \]
(3) There exists
 $1< \sigma \ll {\mathsf {s}}_Y^{\star }$ such that for all
$1< \sigma \ll {\mathsf {s}}_Y^{\star }$ such that for all  $y\in Y_0$ and for all
$y\in Y_0$ and for all  $h\in H$ with
$h\in H$ with  $\|h\|\ge 2$ and
$\|h\|\ge 2$ and  $yh\in Y_0$,
$yh\in Y_0$,
 \[ \sigma^{-1} F_{s} (y) \le F_{s}(yh) \le \sigma F_{s}(y). \]
\[ \sigma^{-1} F_{s} (y) \le F_{s}(yh) \le \sigma F_{s}(y). \]
Finally we mention that the reason that we can take the exponent ![]() $s$ arbitrarily close to
$s$ arbitrarily close to ![]() $\delta _Y$ lies in the two ingredients of our proof: first, the linear algebra lemma (Lemma 5.6) is obtained for all
$\delta _Y$ lies in the two ingredients of our proof: first, the linear algebra lemma (Lemma 5.6) is obtained for all ![]() $\delta _Y/3\le s<\delta _Y$; and second, for any
$\delta _Y/3\le s<\delta _Y$; and second, for any ![]() $y\in Y\cap X_0$, we can find
$y\in Y\cap X_0$, we can find ![]() $|r|<1$ so that
$|r|<1$ so that ![]() $yu_r\in X_0$ and the height of
$yu_r\in X_0$ and the height of ![]() $yu_r$ can be lowered to be
$yu_r$ can be lowered to be ![]() $O(1)$ by the geodesic flow of time comparable to the logarithmic height of
$O(1)$ by the geodesic flow of time comparable to the logarithmic height of ![]() $y$; see Lemma 8.4 for the precise statement.
$y$; see Lemma 8.4 for the precise statement.
Organization
We end this introduction with an outline of the paper. In §2, we fix some notation and conventions to be used throughout the paper. In § 3, we show the finiteness of the tight area of a properly immersed geodesic plane. In § 4, we show the finiteness of the shadow constant of a closed ![]() $H$-orbit. In § 5, we prove a lemma from linear algebra; this lemma is a key ingredient to prove a local version of our main inequality. Section 6 is devoted to the study of the height function in
$H$-orbit. In § 5, we prove a lemma from linear algebra; this lemma is a key ingredient to prove a local version of our main inequality. Section 6 is devoted to the study of the height function in ![]() $X_0$. In § 7, the definition of the Markov operator and a basic property of this operator are discussed. In § 8, we prove the return lemma, and use it to obtain a uniform control on the number of sheets of
$X_0$. In § 7, the definition of the Markov operator and a basic property of this operator are discussed. In § 8, we prove the return lemma, and use it to obtain a uniform control on the number of sheets of ![]() $Z$ in a neighborhood of
$Z$ in a neighborhood of ![]() $y$. In § 9, we construct the desired Margulis function and prove the main inequalities. In § 10, we give a proof of Theorem 1.5. In Appendix A, we provide a proof of Theorem 1.1.
$y$. In § 9, we construct the desired Margulis function and prove the main inequalities. In § 10, we give a proof of Theorem 1.5. In Appendix A, we provide a proof of Theorem 1.1.
2. Notation and preliminaries
In this section, we review some definitions and introduce notation which will be used throughout the paper.
We set ![]() $G=\operatorname {PSL}_2(\mathbb {C})\simeq \operatorname {Isom}^+(\mathbb {H}^3)$, and
$G=\operatorname {PSL}_2(\mathbb {C})\simeq \operatorname {Isom}^+(\mathbb {H}^3)$, and ![]() $H=\operatorname {PSL}_2(\mathbb {R})$. We fix
$H=\operatorname {PSL}_2(\mathbb {R})$. We fix ![]() $\mathbb {H}^2\subset \mathbb {H}^3$ with an orientation so that
$\mathbb {H}^2\subset \mathbb {H}^3$ with an orientation so that ![]() $\{g\in G: g(\mathbb {H}^2)=\mathbb {H}^2\}=H$. Let
$\{g\in G: g(\mathbb {H}^2)=\mathbb {H}^2\}=H$. Let ![]() $A$ denote the following one-parameter subgroup of
$A$ denote the following one-parameter subgroup of ![]() $G$:
$G$:
Set ![]() $K_0=\operatorname {PSU}(2)$ and
$K_0=\operatorname {PSU}(2)$ and ![]() $M_0$ the centralizer of
$M_0$ the centralizer of ![]() $A$ in
$A$ in ![]() $K_0$. We fix a point
$K_0$. We fix a point ![]() $o\in \mathbb {H}^2\subset \mathbb {H}^3$ and a unit tangent vector
$o\in \mathbb {H}^2\subset \mathbb {H}^3$ and a unit tangent vector ![]() $v_{o}\in \operatorname {T}_{o}(\mathbb {H}^3)$ so that their stabilizer subgroups are
$v_{o}\in \operatorname {T}_{o}(\mathbb {H}^3)$ so that their stabilizer subgroups are ![]() $K_0$ and
$K_0$ and ![]() $M_0$ respectively. The isometric action of
$M_0$ respectively. The isometric action of ![]() $G$ on
$G$ on ![]() $\mathbb {H}^3$ induces identifications
$\mathbb {H}^3$ induces identifications ![]() $G/K_0=\mathbb {H}^3$,
$G/K_0=\mathbb {H}^3$, ![]() $G/M_0=\operatorname {T}^1 \mathbb {H}^3$, and
$G/M_0=\operatorname {T}^1 \mathbb {H}^3$, and ![]() $G=\operatorname {F}\mathbb {H}^3$ where
$G=\operatorname {F}\mathbb {H}^3$ where ![]() $\operatorname {T}^1 \mathbb {H}^3$ and
$\operatorname {T}^1 \mathbb {H}^3$ and ![]() $\operatorname {F}\! \mathbb {H}^3$ denote, respectively, the unit tangent bundle and the oriented frame bundle over
$\operatorname {F}\! \mathbb {H}^3$ denote, respectively, the unit tangent bundle and the oriented frame bundle over ![]() $\mathbb {H}^3$. Note also that
$\mathbb {H}^3$. Note also that ![]() $H\cap K_0=\operatorname {PSO(2)}$ and that
$H\cap K_0=\operatorname {PSO(2)}$ and that ![]() $H(o)= \mathbb {H}^2$.
$H(o)= \mathbb {H}^2$.
The right translation action of ![]() $A$ on
$A$ on ![]() $G$ induces the geodesic/frame flow on
$G$ induces the geodesic/frame flow on ![]() $\operatorname {T}^1 \mathbb {H}^3$ and
$\operatorname {T}^1 \mathbb {H}^3$ and ![]() $\operatorname {F}\! \mathbb {H}^3$, respectively. Let
$\operatorname {F}\! \mathbb {H}^3$, respectively. Let ![]() $v_{o}^{\pm }\in \partial \mathbb {H}^3$ denote the forward and backward end points of the geodesic given by
$v_{o}^{\pm }\in \partial \mathbb {H}^3$ denote the forward and backward end points of the geodesic given by ![]() $v_{o}$. For
$v_{o}$. For ![]() $g\in G$, we define
$g\in G$, we define
Let ![]() $\Gamma < G$ be a discrete torsion-free subgroup. We set
$\Gamma < G$ be a discrete torsion-free subgroup. We set
We denote by ![]() $\pi : X\to M$ the base point projection map. Denote by
$\pi : X\to M$ the base point projection map. Denote by ![]() $\Lambda =\Lambda (\Gamma )$ the limit set of
$\Lambda =\Lambda (\Gamma )$ the limit set of ![]() $\Gamma$. The convex core of
$\Gamma$. The convex core of ![]() $M$ is given by
$M$ is given by ![]() ${\operatorname {core}}\, M=\Gamma \backslash \text {hull} (\Lambda )$. Let
${\operatorname {core}}\, M=\Gamma \backslash \text {hull} (\Lambda )$. Let ![]() $X_0$ denote the renormalized frame bundle
$X_0$ denote the renormalized frame bundle ![]() $\operatorname {RF}\! {M}$, i.e.
$\operatorname {RF}\! {M}$, i.e.
that is, ![]() $X_0$ is the union of all the
$X_0$ is the union of all the ![]() $A$-orbits whose projections to
$A$-orbits whose projections to ![]() $M$ stay inside
$M$ stay inside ![]() ${\operatorname {core}}\, M$. We remark that
${\operatorname {core}}\, M$. We remark that ![]() $X_0$ does not surject onto
$X_0$ does not surject onto ![]() ${\operatorname {core}}\, M$ in general.
${\operatorname {core}}\, M$ in general.
In the whole paper, we assume that ![]() $\Gamma$ is geometrically finite, that is, the unit neighborhood of
$\Gamma$ is geometrically finite, that is, the unit neighborhood of ![]() ${\operatorname {core}}\, M$ has finite volume. This is equivalent to the condition that
${\operatorname {core}}\, M$ has finite volume. This is equivalent to the condition that ![]() $\Lambda$ is the union of the radial limit points and bounded parabolic limit points:
$\Lambda$ is the union of the radial limit points and bounded parabolic limit points: ![]() $\Lambda =\Lambda _{\rm rad}\bigcup \Lambda _{\rm bp}$ (cf. [Reference BowditchBow93, Reference Matsuzaki and TaniguchiMT98]). A point
$\Lambda =\Lambda _{\rm rad}\bigcup \Lambda _{\rm bp}$ (cf. [Reference BowditchBow93, Reference Matsuzaki and TaniguchiMT98]). A point ![]() $\xi \in \Lambda$ is called radial if the projection of a geodesic ray toward to
$\xi \in \Lambda$ is called radial if the projection of a geodesic ray toward to ![]() $\xi$ accumulates on
$\xi$ accumulates on ![]() $M=\Gamma \backslash \mathbb {H}^3$, parabolic if it is fixed by a parabolic element of
$M=\Gamma \backslash \mathbb {H}^3$, parabolic if it is fixed by a parabolic element of ![]() $\Gamma$, and bounded parabolic if it is parabolic and
$\Gamma$, and bounded parabolic if it is parabolic and ![]() $\operatorname {Stab}_\Gamma (\xi )$ acts co-compactly on
$\operatorname {Stab}_\Gamma (\xi )$ acts co-compactly on ![]() $\Lambda -\{\xi \}$. In particular, for
$\Lambda -\{\xi \}$. In particular, for ![]() $\Gamma$ geometrically finite, the set of parabolic limit points
$\Gamma$ geometrically finite, the set of parabolic limit points ![]() $\Lambda _{\rm p}$ is equal to
$\Lambda _{\rm p}$ is equal to ![]() $\Lambda _{\rm bp}$. For
$\Lambda _{\rm bp}$. For ![]() $\xi \in \Lambda _{\rm p}$, the rank of the free abelian subgroup
$\xi \in \Lambda _{\rm p}$, the rank of the free abelian subgroup ![]() $\operatorname {Stab}_\Gamma (\xi )$ is referred to as the rank of
$\operatorname {Stab}_\Gamma (\xi )$ is referred to as the rank of ![]() $\xi$.
$\xi$.
A geometrically finite group ![]() $\Gamma$ is called convex cocompact if
$\Gamma$ is called convex cocompact if ![]() ${\operatorname {core}}\, M$ is compact, or equivalently, if
${\operatorname {core}}\, M$ is compact, or equivalently, if ![]() $\Lambda =\Lambda _{\rm rad}$.
$\Lambda =\Lambda _{\rm rad}$.
We denote by ![]() $N$ the expanding horospherical subgroup of
$N$ the expanding horospherical subgroup of ![]() $G$ for the action of
$G$ for the action of ![]() $A$:
$A$:
For ![]() $\xi \in \Lambda _{\rm p}$, a horoball
$\xi \in \Lambda _{\rm p}$, a horoball ![]() $\tilde {\mathfrak {h}}_{\xi }\subset G$ based at
$\tilde {\mathfrak {h}}_{\xi }\subset G$ based at ![]() $\xi$ is of the form
$\xi$ is of the form
where ![]() $g\in G$ is such that
$g\in G$ is such that ![]() $g^-=\xi$ and
$g^-=\xi$ and ![]() ${A}_{(-\infty,-T]}=\{a_{t}: -\infty < t\le -T\}$. Its image
${A}_{(-\infty,-T]}=\{a_{t}: -\infty < t\le -T\}$. Its image ![]() $\tilde {\mathfrak {h}}_\xi (o)$ in
$\tilde {\mathfrak {h}}_\xi (o)$ in ![]() $\mathbb {H}^3$ is called a horoball in
$\mathbb {H}^3$ is called a horoball in ![]() $\mathbb {H}^3$ based at
$\mathbb {H}^3$ based at ![]() $\xi$. By a horoball
$\xi$. By a horoball ![]() $\mathfrak {h}_\xi$ in
$\mathfrak {h}_\xi$ in ![]() $X$ and in
$X$ and in ![]() $M$, we mean their respective images of horoballs
$M$, we mean their respective images of horoballs ![]() $\tilde {\mathfrak {h}}_{\xi }$ and
$\tilde {\mathfrak {h}}_{\xi }$ and ![]() $\tilde {\mathfrak {h}}_\xi (o)$ in
$\tilde {\mathfrak {h}}_\xi (o)$ in ![]() $X$ and
$X$ and ![]() $M$ under the corresponding projection maps.
$M$ under the corresponding projection maps.
Thick–thin decomposition of  $X_0$
$X_0$
We fix a Riemannian metric ![]() $d$ on
$d$ on ![]() $G$ which induces the hyperbolic metric on
$G$ which induces the hyperbolic metric on ![]() $\mathbb {H}^3$. By abuse of notation, we use
$\mathbb {H}^3$. By abuse of notation, we use ![]() $d$ to denote the distance function on
$d$ to denote the distance function on ![]() $X$ induced by
$X$ induced by ![]() $d$, as well as on
$d$, as well as on ![]() $M$. For a subset
$M$. For a subset ![]() $S\subset \spadesuit$ and
$S\subset \spadesuit$ and ![]() ${\varepsilon }>0$,
${\varepsilon }>0$, ![]() $B_\spadesuit (S, {\varepsilon })$ denotes the set
$B_\spadesuit (S, {\varepsilon })$ denotes the set ![]() $\{x\in \spadesuit : d(x, S)\le {\varepsilon }\}$. When
$\{x\in \spadesuit : d(x, S)\le {\varepsilon }\}$. When ![]() $\spadesuit$ is a subgroup of
$\spadesuit$ is a subgroup of ![]() $G$ and
$G$ and ![]() $S=\{e\}$, we simply write
$S=\{e\}$, we simply write ![]() $B_\spadesuit ({\varepsilon })$ instead of
$B_\spadesuit ({\varepsilon })$ instead of ![]() $B_\spadesuit (S, {\varepsilon })$. When there is no room for confusion for the ambient space
$B_\spadesuit (S, {\varepsilon })$. When there is no room for confusion for the ambient space ![]() $\spadesuit$, we omit the subscript
$\spadesuit$, we omit the subscript ![]() $\spadesuit$.
$\spadesuit$.
For ![]() $p\in M$, we denote by
$p\in M$, we denote by ![]() $\operatorname {inj} p$ the injectivity radius at
$\operatorname {inj} p$ the injectivity radius at ![]() $p\in M$, that is: the supremum
$p\in M$, that is: the supremum ![]() $r>0$ such that the projection map
$r>0$ such that the projection map ![]() $\mathbb {H}^3\to M=\Gamma \backslash \mathbb {H}^3$ is injective on the ball
$\mathbb {H}^3\to M=\Gamma \backslash \mathbb {H}^3$ is injective on the ball ![]() $B_{\mathbb {H}^3}(\tilde p, r)$ where
$B_{\mathbb {H}^3}(\tilde p, r)$ where ![]() $\tilde p\in \mathbb {H}^3$ is such that
$\tilde p\in \mathbb {H}^3$ is such that ![]() $p=[\tilde p]=\tilde p\Gamma$. For
$p=[\tilde p]=\tilde p\Gamma$. For ![]() $S\subset M$ and
$S\subset M$ and ![]() ${\varepsilon }>0$, we call the subsets
${\varepsilon }>0$, we call the subsets ![]() $\{p\in S: \operatorname {inj} (p)\ge {\varepsilon }\}$ and
$\{p\in S: \operatorname {inj} (p)\ge {\varepsilon }\}$ and ![]() $\{p\in S: \operatorname {inj} (p)< {\varepsilon }\}$ the
$\{p\in S: \operatorname {inj} (p)< {\varepsilon }\}$ the ![]() ${\varepsilon }$-thick part and the
${\varepsilon }$-thick part and the ![]() ${\varepsilon }$-thin part of
${\varepsilon }$-thin part of ![]() $S$ respectively.
$S$ respectively.
As ![]() $M$ is geometrically finite,
$M$ is geometrically finite, ![]() ${\operatorname {core}}\, M$ is contained in a union of its
${\operatorname {core}}\, M$ is contained in a union of its ![]() ${\varepsilon }$-thick part
${\varepsilon }$-thick part ![]() $({\operatorname {core}}\, M)_{\varepsilon }$ and finitely many disjoint horoballs for all small
$({\operatorname {core}}\, M)_{\varepsilon }$ and finitely many disjoint horoballs for all small ![]() ${\varepsilon }>0$ (cf. [Reference Matsuzaki and TaniguchiMT98]). If
${\varepsilon }>0$ (cf. [Reference Matsuzaki and TaniguchiMT98]). If ![]() $p=gu_sa_{-t}o$ is contained in a horoball
$p=gu_sa_{-t}o$ is contained in a horoball ![]() $\mathfrak {h}_\xi = g N {A}_{( -\infty, -T]}(o)$, then
$\mathfrak {h}_\xi = g N {A}_{( -\infty, -T]}(o)$, then ![]() $\operatorname {inj} (p)\asymp e^{-t}$ for all
$\operatorname {inj} (p)\asymp e^{-t}$ for all ![]() $t\gg T$, this is a standard fact see, e.g. [Reference Kelmer and OhKO21, Proposition 5.1].
$t\gg T$, this is a standard fact see, e.g. [Reference Kelmer and OhKO21, Proposition 5.1].
Let ![]() ${\varepsilon }_M>0$ be the supremum of
${\varepsilon }_M>0$ be the supremum of ![]() ${\varepsilon }$ with respect to which such a decomposition of
${\varepsilon }$ with respect to which such a decomposition of ![]() ${\operatorname {core}}\, M$ holds. We call the
${\operatorname {core}}\, M$ holds. We call the ![]() ${\varepsilon }_M$-thick part of
${\varepsilon }_M$-thick part of ![]() ${\operatorname {core}}\, M$ the compact core of
${\operatorname {core}}\, M$ the compact core of ![]() $M$, and denote by
$M$, and denote by ![]() $M_{{\rm cpt}}$.
$M_{{\rm cpt}}$.
For ![]() $x=[g]\in X$, we denote by
$x=[g]\in X$, we denote by ![]() $\operatorname {inj}(x)$ the injectivity radius of
$\operatorname {inj}(x)$ the injectivity radius of ![]() $\pi (x)\in M$. For
$\pi (x)\in M$. For ![]() $\varepsilon >0$, we set
$\varepsilon >0$, we set
We set ![]() ${\varepsilon }_X={\varepsilon }_M/2$; note that
${\varepsilon }_X={\varepsilon }_M/2$; note that ![]() $X_0-X_{{\varepsilon }_X}$ is either empty or is contained in a union of horoballs in
$X_0-X_{{\varepsilon }_X}$ is either empty or is contained in a union of horoballs in ![]() $X$.
$X$.
Convention
By an absolute constant, we mean a constant which depends at most on ![]() $G$ and
$G$ and ![]() $\Gamma$. We will use the notation
$\Gamma$. We will use the notation ![]() $A\asymp B$ when the ratio between the two lies in
$A\asymp B$ when the ratio between the two lies in ![]() $[C^{-1}, C]$ for some absolute constant
$[C^{-1}, C]$ for some absolute constant ![]() $C\ge 1$. We write
$C\ge 1$. We write ![]() $A\ll B^\star$ (respectively
$A\ll B^\star$ (respectively ![]() $A\asymp B^\star$,
$A\asymp B^\star$, ![]() $A\ll \star B$) to mean that
$A\ll \star B$) to mean that ![]() $A\le C B^L$ (respectively
$A\le C B^L$ (respectively ![]() $C^{-1}B^L\le A\le C B^L$,
$C^{-1}B^L\le A\le C B^L$, ![]() $A\le C\cdot B$) for some absolute constants
$A\le C\cdot B$) for some absolute constants ![]() $C>0$ and
$C>0$ and ![]() $L>0$.
$L>0$.
3. Tight area of a properly immersed geodesic plane
In this section, we show that the tight area of a properly immersed geodesic plane of ![]() $M$ is finite.
$M$ is finite.
For a closed subset ![]() $Q\subset M$, we define the tight neighborhood of
$Q\subset M$, we define the tight neighborhood of ![]() $Q$ by
$Q$ by
We are mainly interested in the tight neighborhood of ![]() ${\operatorname {core}}\, M$. If
${\operatorname {core}}\, M$. If ![]() $M$ is convex cocompact,
$M$ is convex cocompact, ![]() $\mathcal {N}({\operatorname {core}}\, M)$ is compact. In order to describe the shape of
$\mathcal {N}({\operatorname {core}}\, M)$ is compact. In order to describe the shape of ![]() $\mathcal {N}({\operatorname {core}}\, M)$ in the presence of cusps, fix a set
$\mathcal {N}({\operatorname {core}}\, M)$ in the presence of cusps, fix a set ![]() $\xi _1, \ldots, \xi _\ell$ of
$\xi _1, \ldots, \xi _\ell$ of ![]() $\Gamma$-representatives of
$\Gamma$-representatives of ![]() $\Lambda _{\rm p}$, cf. [Reference Matsuzaki and TaniguchiMT98]. Then
$\Lambda _{\rm p}$, cf. [Reference Matsuzaki and TaniguchiMT98]. Then ![]() ${\operatorname {core}}\, M$ is contained in the union of
${\operatorname {core}}\, M$ is contained in the union of ![]() $M_{\rm cpt}$ and a disjoint union
$M_{\rm cpt}$ and a disjoint union ![]() $\bigcup \mathfrak {h}_{\xi _i}$ of horoballs based at the
$\bigcup \mathfrak {h}_{\xi _i}$ of horoballs based at the ![]() $\xi _i$s.
$\xi _i$s.
Consider the upper half-space model ![]() $\mathbb {H}^3=\{(x_1, x_2,y): y>0\}=\mathbb {R}^2\times \mathbb {R}_{>0}$, and let
$\mathbb {H}^3=\{(x_1, x_2,y): y>0\}=\mathbb {R}^2\times \mathbb {R}_{>0}$, and let ![]() $\infty \in \Lambda _{\rm p}$. Let
$\infty \in \Lambda _{\rm p}$. Let ![]() $p:\mathbb {H}^3\to M$ denote the canonical projection map. As
$p:\mathbb {H}^3\to M$ denote the canonical projection map. As ![]() $\infty$ is a bounded parabolic fixed point, there exists a bounded rectangle, say,
$\infty$ is a bounded parabolic fixed point, there exists a bounded rectangle, say, ![]() $I\subset \mathbb {R}^2$ and
$I\subset \mathbb {R}^2$ and ![]() $r>0$ (depending on
$r>0$ (depending on ![]() $\infty$) such that:
$\infty$) such that:
(1)
 $p(I\times \{y> r \})\supset \mathcal {N}(\mathfrak {h}_\infty \cap {\operatorname {core}}\, M)$; and
$p(I\times \{y> r \})\supset \mathcal {N}(\mathfrak {h}_\infty \cap {\operatorname {core}}\, M)$; and(2)
 $p( I\times \{r\})\subset B(M_{\rm cpt}, R)$
$p( I\times \{r\})\subset B(M_{\rm cpt}, R)$
where ![]() $R$ depends only on
$R$ depends only on ![]() $M$. We call this set
$M$. We call this set ![]() $\mathfrak {C}_\infty :=I\times \{y\ge r \}$ a chimney for
$\mathfrak {C}_\infty :=I\times \{y\ge r \}$ a chimney for ![]() $\infty$ (cf. Figure 3).
$\infty$ (cf. Figure 3).

Figure 3. Chimney.
Note that increasing ![]() $R$ if necessary, we have
$R$ if necessary, we have
 \begin{equation} \mathcal{N}({\operatorname{core}}\, M)\subset B(M_{\rm cpt}, R) \cup \biggl(\bigcup_{1\le i\le \ell} p(\mathfrak{C}_{\xi_i})\biggr), \end{equation}
\begin{equation} \mathcal{N}({\operatorname{core}}\, M)\subset B(M_{\rm cpt}, R) \cup \biggl(\bigcup_{1\le i\le \ell} p(\mathfrak{C}_{\xi_i})\biggr), \end{equation}
where ![]() $\mathfrak {C}_{\xi _i}$ is a chimney for
$\mathfrak {C}_{\xi _i}$ is a chimney for ![]() $\xi _i$.
$\xi _i$.
Definition 3.2 For a properly immersed geodesic plane ![]() $S$ of
$S$ of ![]() $M$, we define the tight-area of
$M$, we define the tight-area of ![]() $S$ relative to
$S$ relative to ![]() $M$ as follows:
$M$ as follows:
Theorem 3.3 For a properly immersed non-elementary geodesic plane ![]() $S$ of
$S$ of ![]() $M$, we have
$M$, we have
where the implied multiplicative constant depends only on ![]() $M$.
$M$.
Proof. Since no horoball can contain a complete geodesic, it follows that ![]() $S$ intersects the compact core
$S$ intersects the compact core ![]() $M_{{\rm cpt}}$. Therefore,
$M_{{\rm cpt}}$. Therefore,
as ![]() $S\cap M_{\rm cpt}$ contains a hyperbolic disk of radius
$S\cap M_{\rm cpt}$ contains a hyperbolic disk of radius ![]() ${\varepsilon }_X$ (see § 2). This implies the lower bound.
${\varepsilon }_X$ (see § 2). This implies the lower bound.
We now turn to the proof of the upper bound. We use the notation in (3.1). Fix a geodesic plane ![]() $P\subset \mathbb {H}^3$ which covers
$P\subset \mathbb {H}^3$ which covers ![]() $S$ and let
$S$ and let ![]() $\Delta ={\rm Stab}_\Gamma (P)$. Fix a Dirichlet domain
$\Delta ={\rm Stab}_\Gamma (P)$. Fix a Dirichlet domain ![]() $D$ in
$D$ in ![]() $P$ for the action of
$P$ for the action of ![]() $\Delta$. As
$\Delta$. As ![]() $\Delta \backslash P$ is geometrically finite, the Dirichlet domain is a finite sided polygon; hence,
$\Delta \backslash P$ is geometrically finite, the Dirichlet domain is a finite sided polygon; hence, ![]() $D\cap \operatorname {hull} (\Delta )$ has finite area, and the set
$D\cap \operatorname {hull} (\Delta )$ has finite area, and the set ![]() $D-\operatorname {hull} (\Delta )$ is a disjoint union of finitely many flares, where a flare is a region bounded by three geodesics as shown in Figure 4. Fixing a flare
$D-\operatorname {hull} (\Delta )$ is a disjoint union of finitely many flares, where a flare is a region bounded by three geodesics as shown in Figure 4. Fixing a flare ![]() $F\subset D-\operatorname {hull} (\Delta )$, it suffices to show that
$F\subset D-\operatorname {hull} (\Delta )$, it suffices to show that ![]() $\{x\in F: p(x)\in \mathcal {N} ({\operatorname {core}}\, M)\}$ has finite area. As
$\{x\in F: p(x)\in \mathcal {N} ({\operatorname {core}}\, M)\}$ has finite area. As ![]() $S$ is properly immersed, the set
$S$ is properly immersed, the set ![]() $\{x\in F: d(p(x), M_{\rm cpt})\le R\}$ is bounded. Therefore, fixing a chimney
$\{x\in F: d(p(x), M_{\rm cpt})\le R\}$ is bounded. Therefore, fixing a chimney ![]() $\mathfrak {C}_{\xi _i}$ as above, it suffices to show that the set
$\mathfrak {C}_{\xi _i}$ as above, it suffices to show that the set ![]() $\{x\in F: p(x)\in \mathfrak {C}_{\xi _i}\}=F\cap \Gamma \mathfrak {C}_{\xi _i}$ has finite area.
$\{x\in F: p(x)\in \mathfrak {C}_{\xi _i}\}=F\cap \Gamma \mathfrak {C}_{\xi _i}$ has finite area.
Figure 4. Flare ![]() $F$ and
$F$ and ![]() $F_{\varepsilon }$.
$F_{\varepsilon }$.
Without loss of generality, we may assume ![]() $\xi _i=\infty$. We will denote by
$\xi _i=\infty$. We will denote by ![]() $\partial F$ the intersection of the closure of
$\partial F$ the intersection of the closure of ![]() $F$ and
$F$ and ![]() $\partial P$, and let
$\partial P$, and let ![]() $F_{\varepsilon }\subset \overline {F}$ denote the
$F_{\varepsilon }\subset \overline {F}$ denote the ![]() ${\varepsilon }$-neighborhood of
${\varepsilon }$-neighborhood of ![]() $\partial F$ in the Euclidean metric in the unit disc model of
$\partial F$ in the Euclidean metric in the unit disc model of ![]() $\overline {P}$ (cf. Figure 4).
$\overline {P}$ (cf. Figure 4).
Fix ![]() ${\varepsilon }_0>0$ so that
${\varepsilon }_0>0$ so that
such ![]() ${\varepsilon }_0$ exists, as
${\varepsilon }_0$ exists, as ![]() $S$ is a proper immersion. Writing
$S$ is a proper immersion. Writing ![]() $\mathfrak {C}_\infty =I\times \{y\ge r\}$ as above, let
$\mathfrak {C}_\infty =I\times \{y\ge r\}$ as above, let ![]() $H_\infty :=\mathbb {R}^2\times \{y>r\}$, and set
$H_\infty :=\mathbb {R}^2\times \{y>r\}$, and set ![]() $\Gamma _\infty :=\operatorname {Stab}_\Gamma (\infty )$.
$\Gamma _\infty :=\operatorname {Stab}_\Gamma (\infty )$.
We claim that
Suppose not. Since ![]() $\Gamma H_\infty$ is closed in the space of all horoballs in
$\Gamma H_\infty$ is closed in the space of all horoballs in ![]() $\mathbb {H}^3$, there exists a sequence of distinct
$\mathbb {H}^3$, there exists a sequence of distinct ![]() $\gamma _i(\infty )\in \Gamma (\infty )$ such that
$\gamma _i(\infty )\in \Gamma (\infty )$ such that ![]() $F_{{\varepsilon }_0/2}\cap \gamma _i \mathfrak {C}_\infty \ne \emptyset$ and the size of the horoballs
$F_{{\varepsilon }_0/2}\cap \gamma _i \mathfrak {C}_\infty \ne \emptyset$ and the size of the horoballs ![]() $\gamma _i H_\infty$ goes to
$\gamma _i H_\infty$ goes to ![]() $0$ in the Euclidean metric in the ball model of
$0$ in the Euclidean metric in the ball model of ![]() $\mathbb {H}^3$. Note that if
$\mathbb {H}^3$. Note that if ![]() $\infty$ has rank
$\infty$ has rank ![]() $2$, then
$2$, then ![]() $\Gamma _\infty (I\times \{r\})=\mathbb {R}^2\times \{r\}$ and that if
$\Gamma _\infty (I\times \{r\})=\mathbb {R}^2\times \{r\}$ and that if ![]() $\infty$ has rank
$\infty$ has rank ![]() $1$, then
$1$, then ![]() $\Gamma _\infty (I\times \{r\})$ contains a region between two parallel horocycles in
$\Gamma _\infty (I\times \{r\})$ contains a region between two parallel horocycles in ![]() $\mathbb {R}^2\times \{r\}$. Since
$\mathbb {R}^2\times \{r\}$. Since ![]() $P\cap \gamma _i \mathfrak {C}_\infty \ne \emptyset$, it follows that
$P\cap \gamma _i \mathfrak {C}_\infty \ne \emptyset$, it follows that ![]() $P\cap \gamma _i (\Gamma _\infty (I \times \{r\})) \ne \emptyset$. Moreover, if
$P\cap \gamma _i (\Gamma _\infty (I \times \{r\})) \ne \emptyset$. Moreover, if ![]() $i$ is large enough so that the Euclidean size of
$i$ is large enough so that the Euclidean size of ![]() $\gamma _i H_\infty$ is smaller than
$\gamma _i H_\infty$ is smaller than ![]() ${\varepsilon }_0/2$, the condition
${\varepsilon }_0/2$, the condition ![]() $F_{{\varepsilon }_0/2} \cap \gamma _i \mathfrak {C}_\infty \ne \emptyset$ implies that
$F_{{\varepsilon }_0/2} \cap \gamma _i \mathfrak {C}_\infty \ne \emptyset$ implies that ![]() $F_{{\varepsilon }_0} \cap \gamma _i (\Gamma _\infty (I \times \{r\})) \ne \emptyset$. This yields a contradiction to (3.4) since
$F_{{\varepsilon }_0} \cap \gamma _i (\Gamma _\infty (I \times \{r\})) \ne \emptyset$. This yields a contradiction to (3.4) since ![]() $p(I\times \{r\})$ is contained in the
$p(I\times \{r\})$ is contained in the ![]() $R$-neighborhood of
$R$-neighborhood of ![]() $M_{\rm cpt}$, proving the claim.
$M_{\rm cpt}$, proving the claim.
By Claim 3.5, it is now enough to show that, fixing a horoball ![]() $\gamma H_\infty$, the intersection
$\gamma H_\infty$, the intersection ![]() $F_{{\varepsilon }_0}\cap \gamma \Gamma _\infty \mathfrak {C}_\infty$ has finite area. Suppose that
$F_{{\varepsilon }_0}\cap \gamma \Gamma _\infty \mathfrak {C}_\infty$ has finite area. Suppose that ![]() $F_{{\varepsilon }_0}\cap \gamma \Gamma _\infty \mathfrak {C}_\infty$ is unbounded in
$F_{{\varepsilon }_0}\cap \gamma \Gamma _\infty \mathfrak {C}_\infty$ is unbounded in ![]() $P$; otherwise the claim is clear. Without loss of generality, we may assume
$P$; otherwise the claim is clear. Without loss of generality, we may assume ![]() $\gamma =e$, by replacing
$\gamma =e$, by replacing ![]() $P$ by
$P$ by ![]() $\gamma ^{-1}P$ if necessary. If
$\gamma ^{-1}P$ if necessary. If ![]() $\infty \notin \partial P$, then
$\infty \notin \partial P$, then ![]() $F_{{\varepsilon }_0}\cap \Gamma _\infty \mathfrak {C}_\infty$, being contained in
$F_{{\varepsilon }_0}\cap \Gamma _\infty \mathfrak {C}_\infty$, being contained in ![]() $P\cap H_\infty$, is a bounded subset of
$P\cap H_\infty$, is a bounded subset of ![]() $P$, which contradicts our supposition. Therefore,
$P$, which contradicts our supposition. Therefore, ![]() $\infty \in \partial P$. Then, as
$\infty \in \partial P$. Then, as ![]() $F_{{\varepsilon }_0}\cap \Gamma _\infty \mathfrak {C}_\infty \subset F_{{\varepsilon }_0}\cap H_\infty$ is unbounded, we have
$F_{{\varepsilon }_0}\cap \Gamma _\infty \mathfrak {C}_\infty \subset F_{{\varepsilon }_0}\cap H_\infty$ is unbounded, we have ![]() $\infty \in \partial F$. Since
$\infty \in \partial F$. Since ![]() $F$ is a flare, it follows that
$F$ is a flare, it follows that ![]() $\infty$ is not a limit point for
$\infty$ is not a limit point for ![]() $\Delta$. This implies that the rank of
$\Delta$. This implies that the rank of ![]() $\infty$ in
$\infty$ in ![]() $\Lambda _{\rm p}$ is
$\Lambda _{\rm p}$ is ![]() $1$ [Reference Oh and ShahOS13, Lemma 6.2]. Therefore
$1$ [Reference Oh and ShahOS13, Lemma 6.2]. Therefore ![]() $\Gamma _\infty \mathfrak {C}_\infty$ is contained in a subset of the form
$\Gamma _\infty \mathfrak {C}_\infty$ is contained in a subset of the form ![]() $T\times \{y\ge r\}$ where
$T\times \{y\ge r\}$ where ![]() $T$ is a strip between two parallel lines
$T$ is a strip between two parallel lines ![]() $L_1, L_2$ in
$L_1, L_2$ in ![]() $\mathbb {R}^2$. Since
$\mathbb {R}^2$. Since ![]() $\infty$ is not a limit point for
$\infty$ is not a limit point for ![]() $\Delta$, the vertical plane
$\Delta$, the vertical plane ![]() $P$ is not parallel to the
$P$ is not parallel to the ![]() $L_i$. Therefore, the intersection
$L_i$. Therefore, the intersection ![]() $F_{{\varepsilon }_0}\cap \Gamma _\infty \mathfrak {C}_\infty$, being a subset of
$F_{{\varepsilon }_0}\cap \Gamma _\infty \mathfrak {C}_\infty$, being a subset of ![]() $P\cap (T\times \{y\ge r\})$, is contained in a cusp-like region, isometric to
$P\cap (T\times \{y\ge r\})$, is contained in a cusp-like region, isometric to ![]() $\{(x,y)\in \mathbb {H}^2: y\ge r\}$ and
$\{(x,y)\in \mathbb {H}^2: y\ge r\}$ and ![]() $x$ is also bounded from above and below (recall that
$x$ is also bounded from above and below (recall that ![]() $P$ is not parallel to the
$P$ is not parallel to the ![]() $L_i$). This finishes the proof.
$L_i$). This finishes the proof.
The proof of the above theorem demonstrates that the portion of ![]() $S$, especially of the flares of
$S$, especially of the flares of ![]() $S$, staying in the tight neighborhood of
$S$, staying in the tight neighborhood of ![]() ${\operatorname {core}}\, M$ can go to infinity only in cusp-like shapes, by visiting the chimneys of horoballs of
${\operatorname {core}}\, M$ can go to infinity only in cusp-like shapes, by visiting the chimneys of horoballs of ![]() ${\operatorname {core}}\, M$ (Figure 1). This is not true any more if we replace the tight neighborhood of
${\operatorname {core}}\, M$ (Figure 1). This is not true any more if we replace the tight neighborhood of ![]() ${\operatorname {core}}\, M$ by the unit neighborhood of
${\operatorname {core}}\, M$ by the unit neighborhood of ![]() ${\operatorname {core}}\, M$. More precisely if
${\operatorname {core}}\, M$. More precisely if ![]() $\Lambda$ contains a parabolic limit point of rank one which is not stabilized by any element of
$\Lambda$ contains a parabolic limit point of rank one which is not stabilized by any element of ![]() $\pi _1(S)$, then some region of
$\pi _1(S)$, then some region of ![]() $S$ with infinite area can stay inside the unit neighborhood of
$S$ with infinite area can stay inside the unit neighborhood of ![]() ${\operatorname {core}}\, M$. This situation may be compared to the presence of divergent geodesics in finite area setting.
${\operatorname {core}}\, M$. This situation may be compared to the presence of divergent geodesics in finite area setting.
4. Shadow constants
In this section, fixing a closed non-elementary ![]() $H$-orbit
$H$-orbit ![]() $Y$ in
$Y$ in ![]() $X$, we recall the definition of Patterson–Sullivan measures
$X$, we recall the definition of Patterson–Sullivan measures ![]() $\mu _y$ on horocycles in
$\mu _y$ on horocycles in ![]() $Y$, and relate its density with the shadow constant
$Y$, and relate its density with the shadow constant ![]() $\mathsf {s}_Y$, which we show is a finite number.
$\mathsf {s}_Y$, which we show is a finite number.
Set ![]() $\Delta _Y:=\operatorname {Stab}_H(y_0)$ to be the stabilizer of a point
$\Delta _Y:=\operatorname {Stab}_H(y_0)$ to be the stabilizer of a point ![]() $y_0\in Y$; note that despite the notation,
$y_0\in Y$; note that despite the notation, ![]() $\Delta _Y$ is uniquely determined up to a conjugation by an element of
$\Delta _Y$ is uniquely determined up to a conjugation by an element of ![]() $H$. As
$H$. As ![]() $\Gamma$ is geometrically finite and
$\Gamma$ is geometrically finite and ![]() $Y=Hy_0$ is a closed orbit, the subgroup
$Y=Hy_0$ is a closed orbit, the subgroup ![]() $\Delta _Y$ is a geometrically finite subgroup of
$\Delta _Y$ is a geometrically finite subgroup of ![]() $H$, [Reference Oh and ShahOS13, Theorem 4.7]. We denote by
$H$, [Reference Oh and ShahOS13, Theorem 4.7]. We denote by ![]() $\Lambda _Y\subset \partial \mathbb {H}^2$ the limit set of
$\Lambda _Y\subset \partial \mathbb {H}^2$ the limit set of ![]() $\Delta _Y$. Let
$\Delta _Y$. Let ![]() $0<\delta (Y)\le 1$ denote the critical exponent of
$0<\delta (Y)\le 1$ denote the critical exponent of ![]() $\Delta _Y$, or equivalently, the Hausdorff dimension of
$\Delta _Y$, or equivalently, the Hausdorff dimension of ![]() $\Lambda _Y$.
$\Lambda _Y$.
We denote by ![]() $\{\nu _p=\nu _{Y, p}: p\in \mathbb {H}^2\}$ the Patterson–Sullivan density for
$\{\nu _p=\nu _{Y, p}: p\in \mathbb {H}^2\}$ the Patterson–Sullivan density for ![]() $\Delta _Y$, normalized so that
$\Delta _Y$, normalized so that ![]() $|\nu _o|=1$. This means that the collection
$|\nu _o|=1$. This means that the collection ![]() $\{\nu _p\}$ consists of Borel measures on
$\{\nu _p\}$ consists of Borel measures on ![]() $\Lambda _Y$ satisfying that for all
$\Lambda _Y$ satisfying that for all ![]() $\gamma \in \Delta _Y$,
$\gamma \in \Delta _Y$, ![]() $p, q \in \mathbb {H}^2$,
$p, q \in \mathbb {H}^2$, ![]() $\xi \in \Lambda _Y$,
$\xi \in \Lambda _Y$,
where ![]() $\beta _\xi (\cdot, \cdot )$ denotes the Busemann function. In what follows we will refer to the first identity above as
$\beta _\xi (\cdot, \cdot )$ denotes the Busemann function. In what follows we will refer to the first identity above as ![]() $\Gamma$-conformality of
$\Gamma$-conformality of ![]() $\{\nu _p\}$.
$\{\nu _p\}$.
As ![]() $\Delta _Y\!$ is geometrically finite, there exists a unique Patterson–Sullivan density up to a constant multiple.
$\Delta _Y\!$ is geometrically finite, there exists a unique Patterson–Sullivan density up to a constant multiple.
PS-measures on  $U$-orbits
$U$-orbits
Set
which is the expanding horocylic subgroup of ![]() $H$. Using the parametrization
$H$. Using the parametrization ![]() ${r}\mapsto u_{r}$, we may identify
${r}\mapsto u_{r}$, we may identify ![]() $U$ with
$U$ with ![]() $\mathbb {R}$. Note that for all
$\mathbb {R}$. Note that for all ![]() $r,t\in \mathbb {R}$,
$r,t\in \mathbb {R}$,
For any ![]() $h\in H$, the restriction of the visual map
$h\in H$, the restriction of the visual map ![]() $g\mapsto g^+$ is a diffeomorphism between
$g\mapsto g^+$ is a diffeomorphism between ![]() $hU$ and
$hU$ and ![]() $\partial \mathbb {H}^2-\{h^-\}$. Using this diffeomorphism, we can define a measure
$\partial \mathbb {H}^2-\{h^-\}$. Using this diffeomorphism, we can define a measure ![]() $\mu _{hU}$ on
$\mu _{hU}$ on ![]() $hU$:
$hU$:
this is independent of the choice of ![]() $p\in \mathbb {H}^2$. We simply write
$p\in \mathbb {H}^2$. We simply write ![]() $d\mu _{h}({r})$ for
$d\mu _{h}({r})$ for ![]() $d \mu _{hU} (hu_{r} )$. Note that these measures depend on the
$d \mu _{hU} (hu_{r} )$. Note that these measures depend on the ![]() $U$-orbits but not on the individual points. By the
$U$-orbits but not on the individual points. By the ![]() $\Delta _Y$-invariance and the conformal property of the PS-density, we have
$\Delta _Y$-invariance and the conformal property of the PS-density, we have
for any ![]() $\gamma \in \Delta _Y$ and for any bounded Borel set
$\gamma \in \Delta _Y$ and for any bounded Borel set ![]() $\mathcal {O}\subset \mathbb {R}$; therefore
$\mathcal {O}\subset \mathbb {R}$; therefore ![]() $\mu _{y}(\mathcal {O})$ is well defined for
$\mu _{y}(\mathcal {O})$ is well defined for ![]() $y\in \Delta _Y\backslash H$.
$y\in \Delta _Y\backslash H$.
For any ![]() $y\in \Delta _Y\backslash H$ and any
$y\in \Delta _Y\backslash H$ and any ![]() $t\in \mathbb {R}$, we have
$t\in \mathbb {R}$, we have
Set
where ![]() $h^{\pm }= \lim _{t\to \pm \infty } ha_t(o)$.
$h^{\pm }= \lim _{t\to \pm \infty } ha_t(o)$.
Shadow constant
As in the introduction, we define the modified critical exponent of ![]() $Y$:
$Y$:
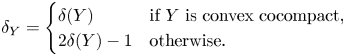 \begin{equation} \delta_Y= \begin{cases} \delta(Y) & \text{if $Y$ is convex cocompact,} \\ 2\delta(Y)-1 & \text{otherwise.}\end{cases} \end{equation}
\begin{equation} \delta_Y= \begin{cases} \delta(Y) & \text{if $Y$ is convex cocompact,} \\ 2\delta(Y)-1 & \text{otherwise.}\end{cases} \end{equation}
If ![]() $Y$ has a cusp, then
$Y$ has a cusp, then ![]() $\delta (Y)>1/2$, and hence
$\delta (Y)>1/2$, and hence ![]() $0<\delta _Y \le \delta (Y)\le 1$.
$0<\delta _Y \le \delta (Y)\le 1$.
Define
the range ![]() $0< r\leq 2$ is motivated by our applications later; see e.g. (7.13).
$0< r\leq 2$ is motivated by our applications later; see e.g. (7.13).
Recall the shadow constant ![]() $\mathsf {s}_Y=\sup _{0<{\varepsilon }\le 1/2} \mathsf {s}_Y({\varepsilon })$ in (1.8) where
$\mathsf {s}_Y=\sup _{0<{\varepsilon }\le 1/2} \mathsf {s}_Y({\varepsilon })$ in (1.8) where
where ![]() $[\xi, \Lambda _Y]$ is the union of all geodesics connecting
$[\xi, \Lambda _Y]$ is the union of all geodesics connecting ![]() $\xi$ to a point in
$\xi$ to a point in ![]() $\Lambda _Y$, and
$\Lambda _Y$, and ![]() $B_p(\xi,\cdot )$ is as in (4.10).
$B_p(\xi,\cdot )$ is as in (4.10).
The rest of this section is devoted to the proof of the following theorem using a uniform version of Sullivan's shadow lemma.
Theorem 4.8 We have
In principle, this definition of ![]() $\mathsf {s}_Y$ involves making a choice of
$\mathsf {s}_Y$ involves making a choice of ![]() $\Delta _Y=\operatorname {Stab}_H(y_0)$, i.e. the choice of
$\Delta _Y=\operatorname {Stab}_H(y_0)$, i.e. the choice of ![]() $y_0\in Y$, as
$y_0\in Y$, as ![]() $\Lambda _Y$ is the limit set of
$\Lambda _Y$ is the limit set of ![]() $\Delta _Y$. However, we observe the following.
$\Delta _Y$. However, we observe the following.
Lemma 4.9 The constant ![]() $\mathsf {s}_Y$ is independent of the choice of
$\mathsf {s}_Y$ is independent of the choice of ![]() $y_0\in Y$.
$y_0\in Y$.
Proof. Let ![]() $y=y_0h^{-1}\in Y$ for
$y=y_0h^{-1}\in Y$ for ![]() $h\in H$. Define
$h\in H$. Define ![]() $\mathsf {s}'_Y$ similar to
$\mathsf {s}'_Y$ similar to ![]() $\mathsf {s}_Y$ using
$\mathsf {s}_Y$ using ![]() $\Delta _Y'={\rm Stab}_H(y)=h\Delta _Yh^{-1}$ and put
$\Delta _Y'={\rm Stab}_H(y)=h\Delta _Yh^{-1}$ and put ![]() $\nu '_p:=h_*\nu _{h^{-1}p}$ for each
$\nu '_p:=h_*\nu _{h^{-1}p}$ for each ![]() $p\in \mathbb {H}^2$. If
$p\in \mathbb {H}^2$. If ![]() $\xi \in \Lambda _Y$, then
$\xi \in \Lambda _Y$, then
 \begin{align*} &\frac{d \bigl((h\gamma h^{-1})_* \nu_p'\bigr)}{d\nu_p'}(h\xi)=\frac{d \bigl((h\gamma)_* \nu_{h^{-1}p}\bigr)}{dh_*\nu_{h^{-1}p}}(h\xi) =\frac{d \gamma_* \nu_{h^{-1}p}}{d\nu_{h^{-1}p}}(\xi)\\ &\quad =e^{-\delta(Y) \beta_\xi(\gamma^{-1}(h^{-1}p), h^{-1}p)} =e^{-\delta(Y) \beta_{h\xi}(h\gamma^{-1}h^{-1}(p), p)}. \end{align*}
\begin{align*} &\frac{d \bigl((h\gamma h^{-1})_* \nu_p'\bigr)}{d\nu_p'}(h\xi)=\frac{d \bigl((h\gamma)_* \nu_{h^{-1}p}\bigr)}{dh_*\nu_{h^{-1}p}}(h\xi) =\frac{d \gamma_* \nu_{h^{-1}p}}{d\nu_{h^{-1}p}}(\xi)\\ &\quad =e^{-\delta(Y) \beta_\xi(\gamma^{-1}(h^{-1}p), h^{-1}p)} =e^{-\delta(Y) \beta_{h\xi}(h\gamma^{-1}h^{-1}(p), p)}. \end{align*}
Since the limit set of ![]() $\Delta '_Y$ is given by
$\Delta '_Y$ is given by ![]() $h\Lambda _Y$, this implies that the family
$h\Lambda _Y$, this implies that the family ![]() $\{\nu '_p: p\in \mathbb {H}^2\}$ is the Patterson–Sullivan density for
$\{\nu '_p: p\in \mathbb {H}^2\}$ is the Patterson–Sullivan density for ![]() $\Delta '_Y$. Now for any
$\Delta '_Y$. Now for any ![]() $0<{\varepsilon }\leq 1$ and
$0<{\varepsilon }\leq 1$ and ![]() $\xi \in \Lambda _Y$, we have
$\xi \in \Lambda _Y$, we have
It follows that ![]() $\mathsf {s}_Y=\mathsf {s}'_Y$.
$\mathsf {s}_Y=\mathsf {s}'_Y$.
Shadow lemma
Consider the associated hyperbolic plane and its convex core:
We denote by ![]() $C_Y$ the compact core of
$C_Y$ the compact core of ![]() $S_Y$, defined as the minimal connected surface whose complement in
$S_Y$, defined as the minimal connected surface whose complement in ![]() $\operatorname {core}(S_Y)$ is a union of disjoint cusps. If
$\operatorname {core}(S_Y)$ is a union of disjoint cusps. If ![]() $S_Y$ is convex cocompact, then
$S_Y$ is convex cocompact, then ![]() $C_Y=S_Y$. Let
$C_Y=S_Y$. Let
We can write ![]() ${\operatorname {core}}\,(S_Y)$ as the disjoint union of the compact core
${\operatorname {core}}\,(S_Y)$ as the disjoint union of the compact core ![]() $C_0:=C_Y$ and finitely many cusps, say,
$C_0:=C_Y$ and finitely many cusps, say, ![]() $C_1, \ldots, C_m$. Fix a Dirichlet domain
$C_1, \ldots, C_m$. Fix a Dirichlet domain ![]() $\mathcal {F}_Y\subset \mathbb {H}^2$ for
$\mathcal {F}_Y\subset \mathbb {H}^2$ for ![]() $\Delta _Y$ containing the base point
$\Delta _Y$ containing the base point ![]() $o$. For each
$o$. For each ![]() $C_i$,
$C_i$, ![]() $0\le i\le m$, choose the lift
$0\le i\le m$, choose the lift ![]() $\tilde {C}_i\subset \mathcal {F}_Y\cap \text {hull}(\Lambda _Y)$ so that
$\tilde {C}_i\subset \mathcal {F}_Y\cap \text {hull}(\Lambda _Y)$ so that ![]() $\Delta _Y\backslash \Delta _Y \tilde {C}_i=C_i$. In particular,
$\Delta _Y\backslash \Delta _Y \tilde {C}_i=C_i$. In particular, ![]() $\partial \tilde {C}_0$ intersects
$\partial \tilde {C}_0$ intersects ![]() $\tilde {C}_i$ in an interval for
$\tilde {C}_i$ in an interval for ![]() $i\ge 1$. Let
$i\ge 1$. Let ![]() $\xi _i\in \Lambda _Y$ be the base point of the horodisc
$\xi _i\in \Lambda _Y$ be the base point of the horodisc ![]() $\tilde {C}_i$, i.e.
$\tilde {C}_i$, i.e. ![]() $\xi _i=\partial \tilde {C}_i \cap \partial \mathbb {H}^2$. Let
$\xi _i=\partial \tilde {C}_i \cap \partial \mathbb {H}^2$. Let ![]() $F_{\xi _i}\subset \partial \mathbb {H}^2-\{\xi _i\}$ be a minimal closed interval so that
$F_{\xi _i}\subset \partial \mathbb {H}^2-\{\xi _i\}$ be a minimal closed interval so that ![]() $\Lambda _Y-\{\xi _i\}\subset \operatorname {Stab}_{\Delta _Y}(\xi _i) F_{\xi _i}$.
$\Lambda _Y-\{\xi _i\}\subset \operatorname {Stab}_{\Delta _Y}(\xi _i) F_{\xi _i}$.
For ![]() $p\in {}{\mathbb {H}}^2$, let
$p\in {}{\mathbb {H}}^2$, let ![]() $d_p$ denote the Gromov distance on
$d_p$ denote the Gromov distance on ![]() $\partial \mathbb {H}^2$: for
$\partial \mathbb {H}^2$: for ![]() $\xi \ne \eta \in \partial \mathbb {H}^2$,
$\xi \ne \eta \in \partial \mathbb {H}^2$,
where ![]() $q$ is any point on the geodesic connecting
$q$ is any point on the geodesic connecting ![]() $\xi$ and
$\xi$ and ![]() $\eta$. The diameter of
$\eta$. The diameter of ![]() $(\partial \mathbb {H}^2, d_p)$ is equal to
$(\partial \mathbb {H}^2, d_p)$ is equal to ![]() $1$.
$1$.
For any ![]() $h\in H$, we have
$h\in H$, we have ![]() $d_{p}(\xi, \eta )= d_{h(p)}(h(\xi ), h(\eta ))$. For
$d_{p}(\xi, \eta )= d_{h(p)}(h(\xi ), h(\eta ))$. For ![]() $\xi \in \partial \mathbb {H}^2$, and
$\xi \in \partial \mathbb {H}^2$, and ![]() $r>0$, set
$r>0$, set
as was defined in the introduction. Also, denote by ![]() $V(p, \xi, r)$ the set of all
$V(p, \xi, r)$ the set of all ![]() $\eta \in \partial \mathbb {H}^2$ such that the distance between
$\eta \in \partial \mathbb {H}^2$ such that the distance between ![]() $p$ and the orthogonal projection of
$p$ and the orthogonal projection of ![]() $\eta$ onto the geodesic
$\eta$ onto the geodesic ![]() $[p, \xi )$ is at least
$[p, \xi )$ is at least ![]() $r$. Note that
$r$. Note that
see ([Reference SchapiraSch04, Lemma 2.5] and the discussion following that lemma). Therefore,
The following is a uniform version of Sullivan's shadow lemma [Reference SullivanSul84]. The proof of this proposition is similar to the proof of [Reference SchapiraSch04, Theorem 3.2]; since the dependence on the multiplicative constant is important to us, we give a sketch of the proof while making the dependence of constants explicit.
Proposition 4.11 There exists a constant ![]() $c\asymp e^{\star d_Y}$ such that for all
$c\asymp e^{\star d_Y}$ such that for all ![]() $\xi \in \Lambda _Y$,
$\xi \in \Lambda _Y$, ![]() $p\in \tilde {C}_0$, and
$p\in \tilde {C}_0$, and ![]() $t>0$,
$t>0$,
 \begin{align*} c^{-1}\cdot \nu_p(F_{{\xi}_t}) \beta_Y e^{-\delta(Y) t +(1-\delta(Y))d(\xi_t, \Delta_Y(p))} &\le \nu_p(V(p, \xi, t)) \\ &\le c \cdot \nu_p(F_{{\xi}_t}) e^{-\delta(Y) t +(1-\delta(Y))d(\xi_t, \Delta_Y(p))} \end{align*}
\begin{align*} c^{-1}\cdot \nu_p(F_{{\xi}_t}) \beta_Y e^{-\delta(Y) t +(1-\delta(Y))d(\xi_t, \Delta_Y(p))} &\le \nu_p(V(p, \xi, t)) \\ &\le c \cdot \nu_p(F_{{\xi}_t}) e^{-\delta(Y) t +(1-\delta(Y))d(\xi_t, \Delta_Y(p))} \end{align*}
where:
•
 $\{\xi _t\}$ is the unit speed geodesic ray
$\{\xi _t\}$ is the unit speed geodesic ray  $[p,\xi )$ so that
$[p,\xi )$ so that  $d(p, \xi _t)=t$;
$d(p, \xi _t)=t$;•
 $F_{\xi _t}=\partial \mathbb {H}^2$ if
$F_{\xi _t}=\partial \mathbb {H}^2$ if  $\xi _t\in \Delta _Y\tilde {C}_0$, and
$\xi _t\in \Delta _Y\tilde {C}_0$, and  $F_{\xi _t}=F_{\xi _i}$ if
$F_{\xi _t}=F_{\xi _i}$ if  $\xi _t\in \Delta _Y\tilde {C}_i$ for
$\xi _t\in \Delta _Y\tilde {C}_i$ for  $1\le i\le m$;
$1\le i\le m$;•
 $\beta _Y:= \inf _{\eta \in \Lambda _Y, q\in \tilde {C}_0} \nu _q(B_q(\eta, e^{-d_Y}))$.
$\beta _Y:= \inf _{\eta \in \Lambda _Y, q\in \tilde {C}_0} \nu _q(B_q(\eta, e^{-d_Y}))$.
Proof. Let ![]() $p$,
$p$, ![]() $\xi \in \Lambda _Y$ and
$\xi \in \Lambda _Y$ and ![]() $\xi _t$ be as in the statement. By the
$\xi _t$ be as in the statement. By the ![]() $\delta (Y)$-conformality of the PS density, we have
$\delta (Y)$-conformality of the PS density, we have
Therefore it suffices to show
while making the dependence of the implied constant explicit.
Claim A If ![]() $\xi _t\in \Delta _Y \tilde {C}_0$, then
$\xi _t\in \Delta _Y \tilde {C}_0$, then
where the implied constants are absolute.
First note that this implies the claim in the proposition if ![]() $\xi _t\in \Delta _Y \tilde {C}_0$. Indeed
$\xi _t\in \Delta _Y \tilde {C}_0$. Indeed ![]() $d(\xi _t, \Delta _Y(p))\leq d_Y$ and
$d(\xi _t, \Delta _Y(p))\leq d_Y$ and ![]() $F_{\xi _t}=\partial \mathbb {H}^2$ in this case. Moreover, by (4.12), we have
$F_{\xi _t}=\partial \mathbb {H}^2$ in this case. Moreover, by (4.12), we have
where we also used ![]() $|\nu _p|=e^{\star d_Y}$ (recall that
$|\nu _p|=e^{\star d_Y}$ (recall that ![]() $p\in \tilde {C}_0$). Thus the claim in the proposition follows in this case.
$p\in \tilde {C}_0$). Thus the claim in the proposition follows in this case.
We now turn to the proof of Claim A. As ![]() $\xi _t\in \Delta _Y \tilde {C}_0$, there exists
$\xi _t\in \Delta _Y \tilde {C}_0$, there exists ![]() $\gamma \in \Delta _Y$ such that
$\gamma \in \Delta _Y$ such that ![]() ${d(\xi _t, \gamma p) \le d_Y}$. Hence
${d(\xi _t, \gamma p) \le d_Y}$. Hence
 \begin{align*} e^{-\delta(Y) d_Y} \nu_{\xi_t} (V(p, \xi, t)) &\le \nu_{\gamma p} (V(p, \xi, t))= \nu_p (V(\gamma^{-1}p, \gamma^{-1}\xi, t))\\ &\le e^{{\delta(Y)} d_Y} \nu_{\xi_t} (V(p, \xi, t)). \end{align*}
\begin{align*} e^{-\delta(Y) d_Y} \nu_{\xi_t} (V(p, \xi, t)) &\le \nu_{\gamma p} (V(p, \xi, t))= \nu_p (V(\gamma^{-1}p, \gamma^{-1}\xi, t))\\ &\le e^{{\delta(Y)} d_Y} \nu_{\xi_t} (V(p, \xi, t)). \end{align*}
The upper bound in (4.12) follows from the first inequality, while the lower bound follows from the second inequality; indeed
and the latter contains ![]() $B_p(\gamma ^{-1} \xi, e^{-d_Y})$, since
$B_p(\gamma ^{-1} \xi, e^{-d_Y})$, since ![]() $d(p, \gamma ^{-1}\xi _t)\le d_Y$ and
$d(p, \gamma ^{-1}\xi _t)\le d_Y$ and ![]() $d_Y\geq 1$.
$d_Y\geq 1$.
Claim B Let ![]() $\xi$ be a parabolic limit point in
$\xi$ be a parabolic limit point in ![]() $\Lambda _Y$. Assume that for some
$\Lambda _Y$. Assume that for some ![]() $i\ge 1$,
$i\ge 1$, ![]() $\xi _t\in \tilde {C}_i$ for all large
$\xi _t\in \tilde {C}_i$ for all large ![]() $t$.
$t$.
We claim
and
where here and in what follows implied constants are of the form ![]() $e^{\pm \star d_Y}$ unless otherwise is stated explicitly.
$e^{\pm \star d_Y}$ unless otherwise is stated explicitly.
Let ![]() $s_i\ge 0$ be such that
$s_i\ge 0$ be such that ![]() $\xi _{s_i}\in \partial \tilde {C}_i$. Then for all
$\xi _{s_i}\in \partial \tilde {C}_i$. Then for all ![]() $t\ge s_i$,
$t\ge s_i$,
Hence for (4.13), it suffices to show
Note that if we set ![]() $\Delta _{Y,\xi }=\operatorname {Stab}_{\Delta _Y}(\xi )$,
$\Delta _{Y,\xi }=\operatorname {Stab}_{\Delta _Y}(\xi )$,
Let ![]() $F^*_{\xi }$ denote the image of
$F^*_{\xi }$ denote the image of ![]() $F_\xi$ on the horocycle based at
$F_\xi$ on the horocycle based at ![]() $\xi$ passing through
$\xi$ passing through ![]() $p$ via the inverse of the visual map. Since
$p$ via the inverse of the visual map. Since ![]() $p\in \tilde {C}_0$, there exists
$p\in \tilde {C}_0$, there exists ![]() $\gamma \in \Delta _{Y, \xi }$ so that
$\gamma \in \Delta _{Y, \xi }$ so that ![]() $\gamma F^*_{\xi }$ is contained in the closure of
$\gamma F^*_{\xi }$ is contained in the closure of ![]() $\tilde {C}_0$. Hence,
$\tilde {C}_0$. Hence,
We now apply [Reference SchapiraSch04, Lemma 2.9] with ![]() $K=F^*_{\xi }$ and let
$K=F^*_{\xi }$ and let ![]() $K_3$ be as in [Reference SchapiraSch04]. By the definition of
$K_3$ be as in [Reference SchapiraSch04]. By the definition of ![]() $K_3$ given in the proof of [Reference SchapiraSch04, Lemma 2.9], we have
$K_3$ given in the proof of [Reference SchapiraSch04, Lemma 2.9], we have ![]() $K_3\ll \text {diam}\,F^*_{\xi }$ where the implied constant is absolute. Thus, in view of [Reference SchapiraSch04, Lemma 2.9], if
$K_3\ll \text {diam}\,F^*_{\xi }$ where the implied constant is absolute. Thus, in view of [Reference SchapiraSch04, Lemma 2.9], if ![]() $\gamma \in \Delta _{Y, \xi }$ is so that
$\gamma \in \Delta _{Y, \xi }$ is so that ![]() $\gamma F_\xi \cap V(p, \xi, t)\ne \emptyset$, then
$\gamma F_\xi \cap V(p, \xi, t)\ne \emptyset$, then ![]() $d(p, \gamma p)\ge 2t -kd_Y$, where
$d(p, \gamma p)\ge 2t -kd_Y$, where ![]() $k$ is absolute. In consequence,
$k$ is absolute. In consequence,
where the implied constant is absolute.
Now we use the fact that if ![]() $d(p, \gamma p)\ge 2t$, then for all
$d(p, \gamma p)\ge 2t$, then for all ![]() $\eta \in F_\xi$,
$\eta \in F_\xi$,
(cf. proof of [Reference SchapiraSch04, Lemma 2.9]). Since
and ![]() $\nu _{\xi _t}(F_\xi )= e^{-\delta (Y) t}\nu _p(F_\xi )$, we deduce, with multiplicative constant
$\nu _{\xi _t}(F_\xi )= e^{-\delta (Y) t}\nu _p(F_\xi )$, we deduce, with multiplicative constant ![]() $\asymp e^{\delta (Y) d_Y}$,
$\asymp e^{\delta (Y) d_Y}$,
 \begin{align*} \sum_{\gamma \in \Delta_{Y, \xi}, d(p, \gamma p)\ge 2t} \nu_{\xi_t}(\gamma F_\xi) &\asymp \sum_{\gamma \in \Delta_{Y, \xi}, d(p, \gamma p)\ge 2t} e^{2\delta(Y) t -\delta(Y) d(p, \gamma p) } \nu_{\xi_t}(F_\xi) \\ &\asymp \nu_p(F_\xi) e^{\delta(Y) t }\sum_{\gamma \in \Delta_{Y, \xi}, d(p, \gamma p)\ge 2t} e^{-\delta(Y) d(p, \gamma p)}\\ & \asymp \nu_p(F_\xi) e^{(1-\delta(Y)) t } \end{align*}
\begin{align*} \sum_{\gamma \in \Delta_{Y, \xi}, d(p, \gamma p)\ge 2t} \nu_{\xi_t}(\gamma F_\xi) &\asymp \sum_{\gamma \in \Delta_{Y, \xi}, d(p, \gamma p)\ge 2t} e^{2\delta(Y) t -\delta(Y) d(p, \gamma p) } \nu_{\xi_t}(F_\xi) \\ &\asymp \nu_p(F_\xi) e^{\delta(Y) t }\sum_{\gamma \in \Delta_{Y, \xi}, d(p, \gamma p)\ge 2t} e^{-\delta(Y) d(p, \gamma p)}\\ & \asymp \nu_p(F_\xi) e^{(1-\delta(Y)) t } \end{align*}
using ![]() $a_n:=\#\{\gamma \in \Delta _{Y, \xi }: n< d(p, \gamma p)\le n+1\} \asymp e^{n/2}$ in the last estimate. This proves (4.13).
$a_n:=\#\{\gamma \in \Delta _{Y, \xi }: n< d(p, \gamma p)\le n+1\} \asymp e^{n/2}$ in the last estimate. This proves (4.13).
The estimate (4.14) follows similarly now using
and ![]() $\sum _{n=0}^{[2t]} a_n e^{-\delta (Y) n} \asymp e^{(1-2\delta (Y) )t}$.
$\sum _{n=0}^{[2t]} a_n e^{-\delta (Y) n} \asymp e^{(1-2\delta (Y) )t}$.
Note that when ![]() $\xi$ is a parabolic limit point, (4.13) holds with multiplicative constant
$\xi$ is a parabolic limit point, (4.13) holds with multiplicative constant ![]() $\asymp e^{\star d_Y}$ (see the proof of [Reference SchapiraSch04, Proposition 3.4]).
$\asymp e^{\star d_Y}$ (see the proof of [Reference SchapiraSch04, Proposition 3.4]).
As for the remaining case, i.e. ![]() $\xi$ is a radial limit point but
$\xi$ is a radial limit point but ![]() $\xi _t\in \Delta _Y \tilde {C}_i$ for some
$\xi _t\in \Delta _Y \tilde {C}_i$ for some ![]() $i$, one can prove that (4.13) holds with multiplicative constant
$i$, one can prove that (4.13) holds with multiplicative constant ![]() $\asymp e^{\star d_Y}$ (see the proof of [Reference SchapiraSch04, Lemma 3.6]).
$\asymp e^{\star d_Y}$ (see the proof of [Reference SchapiraSch04, Lemma 3.6]).
Proposition 4.16 Fix ![]() $p=p_Y\in \tilde {C}_0$. There exists
$p=p_Y\in \tilde {C}_0$. There exists ![]() $R_Y\asymp e^{\star d_Y}$ such that for all
$R_Y\asymp e^{\star d_Y}$ such that for all ![]() $y\in Y_0$, we have
$y\in Y_0$, we have
where ![]() $\pi$ denotes the base point projection
$\pi$ denotes the base point projection ![]() $\Delta _Y\backslash H =\operatorname {T}^1(S_Y) \to S_Y$.
$\Delta _Y\backslash H =\operatorname {T}^1(S_Y) \to S_Y$.
Proof. The following argument is a slight modification of the proof of [Reference Maucourant and SchapiraMS14, Proposition 5.1]. Since the map ![]() $y\mapsto \mu _y[-1,1]$ is continuous on
$y\mapsto \mu _y[-1,1]$ is continuous on ![]() $Y_0$ and
$Y_0$ and ![]() $\{[h]\in Y_0: h^-\text { is a radial limit point of }\Lambda _Y\}$ is dense in
$\{[h]\in Y_0: h^-\text { is a radial limit point of }\Lambda _Y\}$ is dense in ![]() $Y_0$, it suffices to prove the claim for
$Y_0$, it suffices to prove the claim for ![]() $y=[h]$, assuming that
$y=[h]$, assuming that ![]() $h^-$ is a radial limit point for
$h^-$ is a radial limit point for ![]() $\Delta _Y$.
$\Delta _Y$.
Recall that ![]() ${\mu _y([-1,1])}=e^{\delta (Y) t} {\mu _{ya_{-t}}([-e^{-t}, e^{-t}])}$ for all
${\mu _y([-1,1])}=e^{\delta (Y) t} {\mu _{ya_{-t}}([-e^{-t}, e^{-t}])}$ for all ![]() $t\in \mathbb {R}$. Let
$t\in \mathbb {R}$. Let ![]() $t\ge 0$ be the minimal number so that
$t\ge 0$ be the minimal number so that ![]() $\pi (ya_{-t})\in C_Y$; this exists as
$\pi (ya_{-t})\in C_Y$; this exists as ![]() $h^-$ is a radial limit point. Then
$h^-$ is a radial limit point. Then
Set ![]() $\xi _t=ha_{-t}(o)$. Then
$\xi _t=ha_{-t}(o)$. Then
(cf. [Reference SchapiraSch04, Lemma 4.4]).
Since ![]() $ya_{-t}\in C_Y$,
$ya_{-t}\in C_Y$, ![]() $F_{\xi _t}=\partial \mathbb {H}^2$. So
$F_{\xi _t}=\partial \mathbb {H}^2$. So ![]() $\nu _{\xi _t} (F_{\xi _t} )=|\nu _{\xi _t}|\asymp |\nu _p|$ up to a multiplicative constant
$\nu _{\xi _t} (F_{\xi _t} )=|\nu _{\xi _t}|\asymp |\nu _p|$ up to a multiplicative constant ![]() $e^{\star d_Y}$. Therefore, for some implied constant
$e^{\star d_Y}$. Therefore, for some implied constant ![]() $\asymp e^{\star d_Y}$, we have
$\asymp e^{\star d_Y}$, we have
 \begin{align*} \beta_Y e^{-\delta(Y) t +(1-\delta(Y))d(\pi(y), \pi(ya_{-t}))} |\nu_p| &\ll \nu_{\xi_t}(V(\xi_t, h^+, t)) \\ &\ll e^{-\delta(Y) t +(1-\delta(Y))d(\pi(y), \pi(ya_{-t}))} |\nu_p|. \end{align*}
\begin{align*} \beta_Y e^{-\delta(Y) t +(1-\delta(Y))d(\pi(y), \pi(ya_{-t}))} |\nu_p| &\ll \nu_{\xi_t}(V(\xi_t, h^+, t)) \\ &\ll e^{-\delta(Y) t +(1-\delta(Y))d(\pi(y), \pi(ya_{-t}))} |\nu_p|. \end{align*}
This estimate and (4.17), therefore, imply that
with the implied constant ![]() $\asymp e^{\star d_Y}$, proving the claim.
$\asymp e^{\star d_Y}$, proving the claim.
We use the following result, essentially obtained by Schapira and Maucourant [Reference SullivanSul84, Reference Maucourant and SchapiraMS14].
Corollary 4.18 Fix ![]() $\rho >0$. Then for all
$\rho >0$. Then for all ![]() $0<{\varepsilon }\leq \rho$,
$0<{\varepsilon }\leq \rho$,
where ![]() $R_Y$ is as in Proposition 4.16.
$R_Y$ is as in Proposition 4.16.
Proof. By (4.3), we have ![]() $\mu _y([-{\varepsilon },{\varepsilon }])={\varepsilon }^{\delta (Y)} \mu _{ya_{-\log {\varepsilon }}}([-1,1]).$ Hence the case when
$\mu _y([-{\varepsilon },{\varepsilon }])={\varepsilon }^{\delta (Y)} \mu _{ya_{-\log {\varepsilon }}}([-1,1]).$ Hence the case when ![]() $Y$ is convex cocompact follows from Proposition 4.16.
$Y$ is convex cocompact follows from Proposition 4.16.
Now suppose that ![]() $Y$ has a cusp. Let
$Y$ has a cusp. Let ![]() $y\in Y_0$. Using the triangle inequality, we get that
$y\in Y_0$. Using the triangle inequality, we get that ![]() $d(\pi (ya_{-\log {\varepsilon }}), C_Y)-d(\pi (y), C_Y) \le |\log {\varepsilon }|$. Therefore, by Proposition 4.16, we have
$d(\pi (ya_{-\log {\varepsilon }}), C_Y)-d(\pi (y), C_Y) \le |\log {\varepsilon }|$. Therefore, by Proposition 4.16, we have
 \begin{align*} \frac{\mu_{ya_{-\log {\varepsilon}}}([-1,1])}{\mu_y([-1,1])} &\le R_Y^2 \beta_Y^{-1} \cdot e^{(1-\delta(Y)) (d(\pi(y a_{-\log {\varepsilon}}), C_Y)-d(\pi(y), C_Y) ) }\\ &\le \begin{cases} R_Y^2 \cdot\beta_Y^{-1}\cdot {\varepsilon}^{\delta(Y)-1} & \text{if $0<{\varepsilon} <1$,}\\ R_Y^2 \cdot\beta_Y^{-1}\cdot{\varepsilon}^{1-\delta(Y)} & \text{if ${\varepsilon}\geq 1$.}\end{cases} \end{align*}
\begin{align*} \frac{\mu_{ya_{-\log {\varepsilon}}}([-1,1])}{\mu_y([-1,1])} &\le R_Y^2 \beta_Y^{-1} \cdot e^{(1-\delta(Y)) (d(\pi(y a_{-\log {\varepsilon}}), C_Y)-d(\pi(y), C_Y) ) }\\ &\le \begin{cases} R_Y^2 \cdot\beta_Y^{-1}\cdot {\varepsilon}^{\delta(Y)-1} & \text{if $0<{\varepsilon} <1$,}\\ R_Y^2 \cdot\beta_Y^{-1}\cdot{\varepsilon}^{1-\delta(Y)} & \text{if ${\varepsilon}\geq 1$.}\end{cases} \end{align*}
As a consequence, we have
 \[ \frac{\mu_y([-{\varepsilon},{\varepsilon}])}{{\varepsilon}^{2\delta(Y)-1} \mu_y([-1,1])} \le \begin{cases} R_Y^2 \cdot\beta_Y^{-1} & \text{if $0<{\varepsilon} <1$,}\\ R_Y^2 \cdot\beta_Y^{-1}\cdot\rho^2 & \text{if $\rho\geq 1$ and $1\leq {\varepsilon}\leq \rho$.}\end{cases} \]
\[ \frac{\mu_y([-{\varepsilon},{\varepsilon}])}{{\varepsilon}^{2\delta(Y)-1} \mu_y([-1,1])} \le \begin{cases} R_Y^2 \cdot\beta_Y^{-1} & \text{if $0<{\varepsilon} <1$,}\\ R_Y^2 \cdot\beta_Y^{-1}\cdot\rho^2 & \text{if $\rho\geq 1$ and $1\leq {\varepsilon}\leq \rho$.}\end{cases} \]
Recall from (4.5) that ![]() $\delta _Y=\delta (Y)$ when
$\delta _Y=\delta (Y)$ when ![]() $Y$ is cocompact and
$Y$ is cocompact and ![]() $\delta _Y=2\delta (Y)-1$ otherwise. The above thus establishes the upper bound.
$\delta _Y=2\delta (Y)-1$ otherwise. The above thus establishes the upper bound.
By choosing ![]() $y\in Y_0$ such that
$y\in Y_0$ such that ![]() $d(\pi (ya_{-\log {\varepsilon }}), C_Y)-d(\pi (y), C_Y) =|\log {\varepsilon }|$, we get the lower bound.
$d(\pi (ya_{-\log {\varepsilon }}), C_Y)-d(\pi (y), C_Y) =|\log {\varepsilon }|$, we get the lower bound.
Theorem 4.8 follows from the following proposition.
Proposition 4.19 We have:
(1) for any
 $0<{\varepsilon }\le 1/2$,
$0<{\varepsilon }\le 1/2$,  $0<\mathsf {s}_Y({\varepsilon })<\infty$;
$0<\mathsf {s}_Y({\varepsilon })<\infty$;(2)
 $\mathsf {s}_Y\asymp {\mathsf {p}}_Y \ll {e^{\star d_Y/\delta _Y} } \beta _Y^{-1/\delta _Y}$.
$\mathsf {s}_Y\asymp {\mathsf {p}}_Y \ll {e^{\star d_Y/\delta _Y} } \beta _Y^{-1/\delta _Y}$.
Proof. Let ![]() $y\in Y_0$ and
$y\in Y_0$ and ![]() $h\in H$ be so that
$h\in H$ be so that ![]() $y=[h]$. Fix
$y=[h]$. Fix ![]() $0< r\le 2$. Recall
$0< r\le 2$. Recall
Since ![]() $|\beta _{hu_r^+} (h(o), hu_r(o))|\le d(o, u_r(o))$, we have
$|\beta _{hu_r^+} (h(o), hu_r(o))|\le d(o, u_r(o))$, we have
with the implied constant independent of all ![]() $0< r\le 2$.
$0< r\le 2$.
Since ![]() $d_o(u_r^+, e^+)= d_{h(o)} ((hu_r)^+, h^+)$ where
$d_o(u_r^+, e^+)= d_{h(o)} ((hu_r)^+, h^+)$ where ![]() $e$ is the identity (recall that
$e$ is the identity (recall that ![]() $v_o^+=e^+$), we have
$v_o^+=e^+$), we have
for some ![]() $c>1$ independent of
$c>1$ independent of ![]() $r$ and
$r$ and ![]() $h$.
$h$.
This implies that
as well as
where ![]() $c'>1$ is independent of
$c'>1$ is independent of ![]() $0<{\varepsilon }<1/2$ and
$0<{\varepsilon }<1/2$ and ![]() $h\in H$.
$h\in H$.
First note that by Corollary 4.18, we have
Similarly, using Corollary 4.18, for any ![]() $0<{\varepsilon }\leq 1/2$, we have
$0<{\varepsilon }\leq 1/2$, we have
the choice of the constant ![]() $4$ here is motivated by the definitions of
$4$ here is motivated by the definitions of ![]() $\mathsf {p}_Y$ and
$\mathsf {p}_Y$ and ![]() $\mathsf {s}_Y$ in (4.6) and (4.7), respectively.
$\mathsf {s}_Y$ in (4.6) and (4.7), respectively.
Altogether we conclude that
Taking supremum over ![]() $0<{\varepsilon }\leq 1/2$ and
$0<{\varepsilon }\leq 1/2$ and ![]() $h\in H$ with
$h\in H$ with ![]() $h^\pm \in \Lambda _Y$, we conclude that
$h^\pm \in \Lambda _Y$, we conclude that ![]() $\mathsf {s}_Y\asymp \mathsf {p}_Y$.
$\mathsf {s}_Y\asymp \mathsf {p}_Y$.
The last claim follows from Corollary 4.18.
5. Linear algebra lemma
The goal of this section is to prove the linear algebra lemma (Lemma 5.6) and its slight variant (Lemma 5.13).
In this section, it is more convenient to identify ![]() $G$ as
$G$ as ![]() $\operatorname {SO}(\mathsf {Q})^\circ$ for the quadratic form
$\operatorname {SO}(\mathsf {Q})^\circ$ for the quadratic form
As ![]() $\mathsf {Q}$ has signature
$\mathsf {Q}$ has signature ![]() $(1,3)$,
$(1,3)$, ![]() $\operatorname {PSL}_2(\mathbb {C})\simeq \operatorname {SO}(\mathsf {Q})^\circ$ as real Lie groups. We consider the standard representation of
$\operatorname {PSL}_2(\mathbb {C})\simeq \operatorname {SO}(\mathsf {Q})^\circ$ as real Lie groups. We consider the standard representation of ![]() $G$ on the space
$G$ on the space ![]() $\mathbb {R}^4$ of row vectors and denote the Euclidean norm on
$\mathbb {R}^4$ of row vectors and denote the Euclidean norm on ![]() $\mathbb {R}^4$ by
$\mathbb {R}^4$ by ![]() $\|\cdot \|$. We have
$\|\cdot \|$. We have
 \[ U=\left\{u_r=\begin{pmatrix}1 & 0 & 0 & 0\\ r & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \\ {r^2}/{2} & r & 0 & 1\end{pmatrix}: r\in\mathbb{R}\right\}< H. \]
\[ U=\left\{u_r=\begin{pmatrix}1 & 0 & 0 & 0\\ r & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \\ {r^2}/{2} & r & 0 & 1\end{pmatrix}: r\in\mathbb{R}\right\}< H. \]
Set
Then the restriction of the standard representation of ![]() $G$ to
$G$ to ![]() $H$ induces a representation of
$H$ induces a representation of ![]() $H$ on
$H$ on ![]() $V$, which is isomorphic to the adjoint representation of
$V$, which is isomorphic to the adjoint representation of ![]() $H$ on its Lie algebra
$H$ on its Lie algebra ![]() $\mathfrak {sl}_2(\mathbb {R})$; in particular, it is irreducible.
$\mathfrak {sl}_2(\mathbb {R})$; in particular, it is irreducible.
Note that for each ![]() $t>0$,
$t>0$, ![]() $\mathbb {R} e_2=\{v\in V: va_t=v\}$,
$\mathbb {R} e_2=\{v\in V: va_t=v\}$, ![]() $\mathbb {R} e_1$ is the subspace of all vectors with eigenvalues
$\mathbb {R} e_1$ is the subspace of all vectors with eigenvalues ![]() $>1$, and
$>1$, and ![]() $\mathbb {R}e_4$ is the subspace of all vectors with eigenvalues
$\mathbb {R}e_4$ is the subspace of all vectors with eigenvalues ![]() $<1$.
$<1$.
Let ![]() $p:V\to \mathbb {R}e_1\oplus \mathbb {R}e_2$ and
$p:V\to \mathbb {R}e_1\oplus \mathbb {R}e_2$ and ![]() $p^+: V\to \mathbb {R}e_1$ denote the natural projections. Writing
$p^+: V\to \mathbb {R}e_1$ denote the natural projections. Writing ![]() $v=v_1e_1+v_2e_2+v_4e_4$, a direct computation yields that for any
$v=v_1e_1+v_2e_2+v_4e_4$, a direct computation yields that for any ![]() $r\in \mathbb {R}$,
$r\in \mathbb {R}$,
For a unit vector ![]() $v\in V$ and
$v\in V$ and ![]() ${\varepsilon }>0$, define
${\varepsilon }>0$, define
Lemma 5.2 For all ![]() $0<{\varepsilon }<1/2$ and a unit vector
$0<{\varepsilon }<1/2$ and a unit vector ![]() $v\in V$, we have
$v\in V$, we have
where ![]() $\ell$ denotes the Lebesgue measure on
$\ell$ denotes the Lebesgue measure on ![]() $\mathbb {R}$.
$\mathbb {R}$.
Proof. Since we are allowed to choose the implied constant in the statement, it suffices to prove the lemma for ![]() $0<{\varepsilon }\leq 0.01$.
$0<{\varepsilon }\leq 0.01$.
Writing ![]() $v=v_1e_1+v_2e_2+v_4e_4$, we have
$v=v_1e_1+v_2e_2+v_4e_4$, we have
If ![]() $|v_4|\geq 0.01$, then
$|v_4|\geq 0.01$, then
If ![]() $|v_4|< 0.01$ but
$|v_4|< 0.01$ but ![]() $0.1\leq |v_2|\leq 1$, then for
$0.1\leq |v_2|\leq 1$, then for ![]() $r\in [-1,1]$, we have
$r\in [-1,1]$, we have ![]() $|v_2+v_4r|\ge 0.09$, and hence for all
$|v_2+v_4r|\ge 0.09$, and hence for all ![]() ${\varepsilon }\leq 0.01$,
${\varepsilon }\leq 0.01$,
Now consider the case when ![]() $|v_4|\leq 0.01$ and
$|v_4|\leq 0.01$ and ![]() $|v_2|\leq 0.1$. Then, since
$|v_2|\leq 0.1$. Then, since ![]() $\|v\|=1$, we get that
$\|v\|=1$, we get that ![]() $|v_1|\geq 0.7$. Hence for all
$|v_1|\geq 0.7$. Hence for all ![]() $r\in [-1,1]$,
$r\in [-1,1]$, ![]() $|v_1+v_2r+v_4r^2/2|> 0.5$. In consequence, for all
$|v_1+v_2r+v_4r^2/2|> 0.5$. In consequence, for all ![]() ${\varepsilon }<1/2$,
${\varepsilon }<1/2$,
proving the estimate on ![]() $D(v,{\varepsilon })$. To estimate
$D(v,{\varepsilon })$. To estimate ![]() $D^+(v,{\varepsilon })$, observe that
$D^+(v,{\varepsilon })$, observe that ![]() $p^+(vu_{r})=(v_1+v_2r+ {v_4r^2}/{2})e_1$ is a polynomial map of degree at most
$p^+(vu_{r})=(v_1+v_2r+ {v_4r^2}/{2})e_1$ is a polynomial map of degree at most ![]() $2$. Moreover, since
$2$. Moreover, since ![]() $\|v\|=1$, we have
$\|v\|=1$, we have
Therefore, ![]() $\sup _{{r}\in [-1,1]}\|p^+(vu_{r})\|\gg 1$. The claim about
$\sup _{{r}\in [-1,1]}\|p^+(vu_{r})\|\gg 1$. The claim about ![]() $D^+(v,{\varepsilon })$ now follows using Lagrange's interpolation; see [Reference Brudnyi and GanzburgBG73] for a more general statement.
$D^+(v,{\varepsilon })$ now follows using Lagrange's interpolation; see [Reference Brudnyi and GanzburgBG73] for a more general statement.
For the rest of this section, we fix a closed non-elementary ![]() $H$-orbit
$H$-orbit ![]() $Y$.
$Y$.
Lemma 5.3 There exists an absolute constant ![]() $\hat b_0>0$ for which the following holds: for any
$\hat b_0>0$ for which the following holds: for any ![]() $y\in Y_0$ and
$y\in Y_0$ and ![]() $0<{\varepsilon } <1$, we have
$0<{\varepsilon } <1$, we have
and
where ![]() ${\mathsf {p}}_Y$ is given as in (4.6).
${\mathsf {p}}_Y$ is given as in (4.6).
Proof. By (5.1), each set ![]() $D(v,{\varepsilon })$ and
$D(v,{\varepsilon })$ and ![]() $D^+(v,{\varepsilon })$ consists of at most two intervals. By Lemma 5.2,
$D^+(v,{\varepsilon })$ consists of at most two intervals. By Lemma 5.2, ![]() $D(v,{\varepsilon })$ (respectively
$D(v,{\varepsilon })$ (respectively ![]() $D^+(v,{\varepsilon })$) may be covered by
$D^+(v,{\varepsilon })$) may be covered by ![]() $\ll 1$ many intervals of length
$\ll 1$ many intervals of length ![]() ${\varepsilon }$ (respectively
${\varepsilon }$ (respectively ![]() ${\varepsilon }^{1/2}$). Therefore (5.4) (respectively (5.5)) follows from the definition of
${\varepsilon }^{1/2}$). Therefore (5.4) (respectively (5.5)) follows from the definition of ![]() ${\mathsf {p}}_Y$.
${\mathsf {p}}_Y$.
We use Lemma 5.3 to prove the following lemma which will be crucial in what follows.
Lemma 5.6 (Linear algebra lemma)
For any ![]() $ {\delta _Y}/{3}\le s < {\delta _Y}$,
$ {\delta _Y}/{3}\le s < {\delta _Y}$, ![]() $1\le \rho \le 2$, and
$1\le \rho \le 2$, and ![]() $t>0$, we have
$t>0$, we have
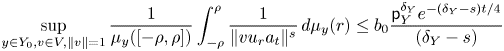 \begin{equation} \sup_{y\in Y_0, v\in V, \|v\|=1} \frac{1}{ \mu_y([-\rho,\rho])}\int_{-\rho}^{\rho} \frac{1}{\| vu_r a_t\|^s} \,d\mu_{y}{} (r) \le b_0 \frac{{\mathsf{p}}_Y^{\delta_Y} e^{-(\delta_Y- s)t/4} }{(\delta_Y-s)} \end{equation}
\begin{equation} \sup_{y\in Y_0, v\in V, \|v\|=1} \frac{1}{ \mu_y([-\rho,\rho])}\int_{-\rho}^{\rho} \frac{1}{\| vu_r a_t\|^s} \,d\mu_{y}{} (r) \le b_0 \frac{{\mathsf{p}}_Y^{\delta_Y} e^{-(\delta_Y- s)t/4} }{(\delta_Y-s)} \end{equation}
where ![]() $b_0\ge 2$ is an absolute constant.
$b_0\ge 2$ is an absolute constant.
Proof. We first claim that it suffices to prove the claim for ![]() $\rho =1$. Indeed, let
$\rho =1$. Indeed, let ![]() $t_\rho =t-\log \rho$ and let
$t_\rho =t-\log \rho$ and let ![]() $y_\rho =ya_{-\log \rho }$, and for every
$y_\rho =ya_{-\log \rho }$, and for every ![]() $v\in V$, let
$v\in V$, let ![]() $v_\rho =va_{-\log \rho }$. Recall also that
$v_\rho =va_{-\log \rho }$. Recall also that ![]() $\mu _y[-r,r]=\rho ^{\delta (Y)} \mu _{ya_{-\log \rho }}{} [-r/\rho,r/\rho ]$ and that
$\mu _y[-r,r]=\rho ^{\delta (Y)} \mu _{ya_{-\log \rho }}{} [-r/\rho,r/\rho ]$ and that ![]() $Y_0$ is
$Y_0$ is ![]() $A$-invariant. Thus,
$A$-invariant. Thus,
 \begin{align*} \frac{1}{ \mu_y([-\rho,\rho])}\int_{-\rho}^{\rho} \frac{1}{\| vu_r a_t\|^s} \,d\mu_{y}(r)&=\frac{1}{ \mu_y([-\rho,\rho])}\int_{-\rho}^{\rho}\frac{1}{\| va_{-\log\rho}u_{\rho^{-1}r} a_{t_\rho}\|^s} \,d\mu_{y}(r) \\ &=\rho^{\delta(Y)}\|v_\rho\|^{-s}\frac{1}{ \mu_{y_\rho}([-1,1])}\int_{-1}^{1}\frac{1}{\| v_\rho' u_{r} a_{t_\rho}\|^s}\,d\mu_{y_\rho}(r) \end{align*}
\begin{align*} \frac{1}{ \mu_y([-\rho,\rho])}\int_{-\rho}^{\rho} \frac{1}{\| vu_r a_t\|^s} \,d\mu_{y}(r)&=\frac{1}{ \mu_y([-\rho,\rho])}\int_{-\rho}^{\rho}\frac{1}{\| va_{-\log\rho}u_{\rho^{-1}r} a_{t_\rho}\|^s} \,d\mu_{y}(r) \\ &=\rho^{\delta(Y)}\|v_\rho\|^{-s}\frac{1}{ \mu_{y_\rho}([-1,1])}\int_{-1}^{1}\frac{1}{\| v_\rho' u_{r} a_{t_\rho}\|^s}\,d\mu_{y_\rho}(r) \end{align*}
where ![]() $v'_\rho =v_\rho /\|v_\rho \|$.
$v'_\rho =v_\rho /\|v_\rho \|$.
Since ![]() $\|v_\rho \|^{-s}\asymp 1$ (with absolute implied constants for
$\|v_\rho \|^{-s}\asymp 1$ (with absolute implied constants for ![]() $1\leq \rho \leq 2$) and
$1\leq \rho \leq 2$) and ![]() $Y_0$ is
$Y_0$ is ![]() $A$-invariant, it thus suffices to prove the lemma for
$A$-invariant, it thus suffices to prove the lemma for ![]() $\rho =1$.
$\rho =1$.
Fix ![]() $0< s<\delta _Y$ and
$0< s<\delta _Y$ and ![]() $t>0$. We observe that for all
$t>0$. We observe that for all ![]() $r\in \mathbb {R}$,
$r\in \mathbb {R}$,
For simplicity, set ![]() $\beta _y:= {1}/{\mu _{y}{}([-1,1])}$. The inequality (5.4) and the first estimate in (5.8) imply that for any
$\beta _y:= {1}/{\mu _{y}{}([-1,1])}$. The inequality (5.4) and the first estimate in (5.8) imply that for any ![]() $0<{\varepsilon }\leq 1$ and any unit vector
$0<{\varepsilon }\leq 1$ and any unit vector ![]() $v\in V$, we have
$v\in V$, we have
 \begin{align*} \beta_y \int_{{r}\in D(v,{\varepsilon} )- D(v, {\varepsilon} /2)} {\| vu_{r}a_t\|^{-s}} d\mu_{y}{}({r}) &\le {\hat b_0 {\mathsf{p}}_Y}^{\delta_Y} {\varepsilon}^{\delta_Y} \cdot ({\varepsilon}/2)^{-s} \\ &\le 2\hat b_0 {\mathsf{p}}_Y^{\delta_Y} {\varepsilon}^{\delta_Y-s}. \end{align*}
\begin{align*} \beta_y \int_{{r}\in D(v,{\varepsilon} )- D(v, {\varepsilon} /2)} {\| vu_{r}a_t\|^{-s}} d\mu_{y}{}({r}) &\le {\hat b_0 {\mathsf{p}}_Y}^{\delta_Y} {\varepsilon}^{\delta_Y} \cdot ({\varepsilon}/2)^{-s} \\ &\le 2\hat b_0 {\mathsf{p}}_Y^{\delta_Y} {\varepsilon}^{\delta_Y-s}. \end{align*}
We write ![]() $D(v,{\varepsilon })=\bigcup _{k=0}^\infty D(v, {\varepsilon }/2^k) -D(v, {\varepsilon }/2^{k+1})$. Now applying the above estimate for each
$D(v,{\varepsilon })=\bigcup _{k=0}^\infty D(v, {\varepsilon }/2^k) -D(v, {\varepsilon }/2^{k+1})$. Now applying the above estimate for each ![]() ${\varepsilon }/2^k$ and summing up the geometric series, we get that for any
${\varepsilon }/2^k$ and summing up the geometric series, we get that for any ![]() $0<{\varepsilon }<1$,
$0<{\varepsilon }<1$,
 \begin{equation} \beta_y \int_{{r}\in D(v, {\varepsilon})} {\| vu_{r}a_t\|^{-s}} \,d\mu_{y}{}({r}) \le \frac{2\hat b_0 {\mathsf{p}}_Y^{\delta_Y} {\varepsilon}^{\delta_Y-s}}{1 -2^{s-\delta_Y}} . \end{equation}
\begin{equation} \beta_y \int_{{r}\in D(v, {\varepsilon})} {\| vu_{r}a_t\|^{-s}} \,d\mu_{y}{}({r}) \le \frac{2\hat b_0 {\mathsf{p}}_Y^{\delta_Y} {\varepsilon}^{\delta_Y-s}}{1 -2^{s-\delta_Y}} . \end{equation} Moreover, using (5.5) and the first estimate in (5.8) again, for any ![]() $\kappa >0$, we have
$\kappa >0$, we have
Finally, the definition of ![]() $D^+(v, \kappa )$ and the second estimate in (5.8) imply
$D^+(v, \kappa )$ and the second estimate in (5.8) imply
Combining (5.9), (5.10), and (5.11) and using the inequality ![]() ${1}/({1-2^{-(\delta _Y-s)}}) \le {2}/({\delta _Y-s})$, we deduce that for any
${1}/({1-2^{-(\delta _Y-s)}}) \le {2}/({\delta _Y-s})$, we deduce that for any ![]() $0<{\varepsilon }, \kappa <1$,
$0<{\varepsilon }, \kappa <1$,
Let ![]() $\varepsilon =e^{-t/4}$ and
$\varepsilon =e^{-t/4}$ and ![]() $\kappa ={\varepsilon }^{2}$. As
$\kappa ={\varepsilon }^{2}$. As ![]() $\delta _Y/3 \le s<\delta _Y$, we have
$\delta _Y/3 \le s<\delta _Y$, we have ![]() $e^{-s/2}\le e^{(s-\delta _Y)/4}$. This yields
$e^{-s/2}\le e^{(s-\delta _Y)/4}$. This yields
as we claimed.
We will extend the upper bound in Lemma 5.6 to all unit vectors ![]() $v\in e_1G$, based on the fact that the vectors in
$v\in e_1G$, based on the fact that the vectors in ![]() $e_1G$ are projectively away from the
$e_1G$ are projectively away from the ![]() $H$-invariant point corresponding to
$H$-invariant point corresponding to ![]() $\mathbb {R} e_3$.
$\mathbb {R} e_3$.
Lemma 5.12 There exists an absolute constant ![]() $b_1>1$ such that for any vector
$b_1>1$ such that for any vector ![]() $v\in e_1G\subset \mathbb {R}^4$,
$v\in e_1G\subset \mathbb {R}^4$,
where ![]() $v_1$ is the projection of
$v_1$ is the projection of ![]() $v\in \mathbb {R}^4$ to
$v\in \mathbb {R}^4$ to ![]() $V=\mathbb {R} e_1\oplus \mathbb {R} e_2\oplus \mathbb {R} e_4$.
$V=\mathbb {R} e_1\oplus \mathbb {R} e_2\oplus \mathbb {R} e_4$.
Proof. Since ![]() $\mathsf {Q}(e_1)=0$ and
$\mathsf {Q}(e_1)=0$ and ![]() $G=\operatorname {SO}(\mathsf {Q})^\circ$, we have
$G=\operatorname {SO}(\mathsf {Q})^\circ$, we have ![]() $\mathsf {Q}(e_1g)=0$ for every
$\mathsf {Q}(e_1g)=0$ for every ![]() $g\in G$. Since
$g\in G$. Since ![]() $\mathsf {Q}(e_3)=-1$, the set
$\mathsf {Q}(e_3)=-1$, the set ![]() $\{\|v\|^{-1} v: v\in e_1G\}$ is a compact subset of the unit sphere in
$\{\|v\|^{-1} v: v\in e_1G\}$ is a compact subset of the unit sphere in ![]() $\mathbb {R}^4$ not containing
$\mathbb {R}^4$ not containing ![]() $\pm e_3$. Therefore there exists an absolute constant
$\pm e_3$. Therefore there exists an absolute constant ![]() $0<\eta <1$ such that if we write
$0<\eta <1$ such that if we write ![]() $v=v_1 +re_3\in e_1G$, then
$v=v_1 +re_3\in e_1G$, then ![]() $|r|\le \eta \|v\|$. Therefore
$|r|\le \eta \|v\|$. Therefore ![]() $\|v_1\|^2=\|v\|^2 -r^2 \ge (1-\eta ^2)\|v\|^2$. Hence it suffices to set
$\|v_1\|^2=\|v\|^2 -r^2 \ge (1-\eta ^2)\|v\|^2$. Hence it suffices to set ![]() $b_1=(1-\eta ^2)^{-1/2}$.
$b_1=(1-\eta ^2)^{-1/2}$.
Lemma 5.13 (Linear algebra lemma II)
For any ![]() $ {\delta _Y}/{3}\le s < {\delta _Y}$,
$ {\delta _Y}/{3}\le s < {\delta _Y}$, ![]() $1\le \rho \le 2$, and
$1\le \rho \le 2$, and ![]() $t>0$, we have
$t>0$, we have
 \[ \sup_{y\in Y_0,v\in e_1G, \|v\|=1} \frac{1}{ \mu_y([-\rho,\rho])}\int_{-\rho}^{\rho} \frac{1}{\| vu_r a_t\|^s} \,d\mu_{y}{} (r) \le b_0 b_1\frac{{\mathsf{p}}_Y^{\delta_Y} e^{-(\delta_Y- s)t/4} }{(\delta_Y-s)} \]
\[ \sup_{y\in Y_0,v\in e_1G, \|v\|=1} \frac{1}{ \mu_y([-\rho,\rho])}\int_{-\rho}^{\rho} \frac{1}{\| vu_r a_t\|^s} \,d\mu_{y}{} (r) \le b_0 b_1\frac{{\mathsf{p}}_Y^{\delta_Y} e^{-(\delta_Y- s)t/4} }{(\delta_Y-s)} \]
where ![]() $b_0\ge 2$ and
$b_0\ge 2$ and ![]() $b_1>1$ are absolute constants as in Lemmas 5.6 and 5.12 respectively.
$b_1>1$ are absolute constants as in Lemmas 5.6 and 5.12 respectively.
Proof. Let ![]() $v\in e_1G$ be a unit vector, and write
$v\in e_1G$ be a unit vector, and write ![]() $v=v_0+v_1$ where
$v=v_0+v_1$ where ![]() $v_0\in \mathbb {R} e_3$ and
$v_0\in \mathbb {R} e_3$ and ![]() $v_1\in V$. Since
$v_1\in V$. Since ![]() $e_3$ is
$e_3$ is ![]() $H$-invariant, we have
$H$-invariant, we have ![]() $vh=v_0+v_1h\in \mathbb {R} e_3\oplus V$ for all
$vh=v_0+v_1h\in \mathbb {R} e_3\oplus V$ for all ![]() $h\in H$. Therefore,
$h\in H$. Therefore,
 \begin{align*}
\frac{1}{\mu_y([-\rho,\rho])}\int_{-\rho}^{\rho}
\frac{1}{\| vu_r a_t\|^s} \,d\mu_y(r)&\leq
\frac{1}{\mu_y([-\rho,\rho])}\int_{-\rho}^{\rho}
\frac{1}{\| v_1u_r a_t\|^s} \,d\mu_y(r)\\ & \le
\frac{b_0{\mathsf{p}}_Y^{\delta_Y} e^{-(\delta_Y-s)t/4}
}{(\delta_Y-s)} \|v_1\|^{-s}\quad \text{by Lemma }\mbox{5.6}\\ &\le \frac{
b_0b_1{\mathsf{p}}_Y^{\delta_Y} e^{-(\delta_Y- s)t/4}
}{(\delta_Y-s)} \|v\|^{-s}\quad\text{by Lemma }\mbox{5.12}.
\end{align*}
\begin{align*}
\frac{1}{\mu_y([-\rho,\rho])}\int_{-\rho}^{\rho}
\frac{1}{\| vu_r a_t\|^s} \,d\mu_y(r)&\leq
\frac{1}{\mu_y([-\rho,\rho])}\int_{-\rho}^{\rho}
\frac{1}{\| v_1u_r a_t\|^s} \,d\mu_y(r)\\ & \le
\frac{b_0{\mathsf{p}}_Y^{\delta_Y} e^{-(\delta_Y-s)t/4}
}{(\delta_Y-s)} \|v_1\|^{-s}\quad \text{by Lemma }\mbox{5.6}\\ &\le \frac{
b_0b_1{\mathsf{p}}_Y^{\delta_Y} e^{-(\delta_Y- s)t/4}
}{(\delta_Y-s)} \|v\|^{-s}\quad\text{by Lemma }\mbox{5.12}.
\end{align*}
6. Height function  $\omega$
$\omega$
In this section we define the height function ![]() $\omega :X_0\to (0, \infty )$ and show that
$\omega :X_0\to (0, \infty )$ and show that ![]() $\omega (x)$ is comparable to the reciprocal of the injectivity radius at
$\omega (x)$ is comparable to the reciprocal of the injectivity radius at ![]() $x$.
$x$.
For this purpose, we continue to realize ![]() $G$ as
$G$ as ![]() $\operatorname {SO}(\mathsf {Q})^\circ$ acting on
$\operatorname {SO}(\mathsf {Q})^\circ$ acting on ![]() $\mathbb {R}^4$ by the standard representation, as in § 5. Observe that
$\mathbb {R}^4$ by the standard representation, as in § 5. Observe that ![]() $\mathsf {Q}(e_1)=0$ and the stabilizer of
$\mathsf {Q}(e_1)=0$ and the stabilizer of ![]() $e_1$ in
$e_1$ in ![]() $G$ is equal to
$G$ is equal to ![]() $M_0N$.
$M_0N$.
Fixing a set of ![]() $\Gamma$-representatives
$\Gamma$-representatives ![]() $\xi _1, \ldots, \xi _\ell$ in
$\xi _1, \ldots, \xi _\ell$ in ![]() $\Lambda _{\rm bp}$, choose elements
$\Lambda _{\rm bp}$, choose elements ![]() $g_i\in G$ so that
$g_i\in G$ so that ![]() $g_i^-=\xi _i$ and
$g_i^-=\xi _i$ and ![]() $\|e_1g_i^{-1}\|=1$; this is possible since
$\|e_1g_i^{-1}\|=1$; this is possible since ![]() $\{g\in G: g^-=\xi _i\}$ is a conjugate of
$\{g\in G: g^-=\xi _i\}$ is a conjugate of ![]() $AM_0N$.
$AM_0N$.
Set
Note that
By Witt's theorem, we have that for each ![]() $i$,
$i$,
Lemma 6.2 For each ![]() $1\le i\le \ell$, the orbit
$1\le i\le \ell$, the orbit ![]() $v_i\Gamma$ is a closed (and hence discrete) subset of
$v_i\Gamma$ is a closed (and hence discrete) subset of ![]() $\mathbb {R}^4$.
$\mathbb {R}^4$.
Proof. The condition ![]() $\xi _i\in \Lambda _{\rm bp}$ implies that
$\xi _i\in \Lambda _{\rm bp}$ implies that ![]() $\Gamma \backslash \Gamma g_i M_0N$ is a closed subset of
$\Gamma \backslash \Gamma g_i M_0N$ is a closed subset of ![]() $X$. Equivalently,
$X$. Equivalently, ![]() $\Gamma g_i M_0N$ as well as
$\Gamma g_i M_0N$ as well as ![]() $\Gamma g_i M_0N g_i^{-1}$ is closed in
$\Gamma g_i M_0N g_i^{-1}$ is closed in ![]() $G$. Therefore, its inverse
$G$. Therefore, its inverse ![]() $g_iM_0 Ng_i^{-1}\Gamma$ is a closed subset of
$g_iM_0 Ng_i^{-1}\Gamma$ is a closed subset of ![]() $G$. In consequence,
$G$. In consequence, ![]() $v_i\Gamma \subset \mathbb {R}^4$ is a closed subset of
$v_i\Gamma \subset \mathbb {R}^4$ is a closed subset of ![]() $v_iG=\{v\in \mathbb {R}^4-\{ 0\}: \mathsf {Q}(v)=0\}$.
$v_iG=\{v\in \mathbb {R}^4-\{ 0\}: \mathsf {Q}(v)=0\}$.
It remains to show that ![]() $v_i\Gamma$ does not accumulate on
$v_i\Gamma$ does not accumulate on ![]() $0$. Suppose on the contrary that there exists an infinite sequence
$0$. Suppose on the contrary that there exists an infinite sequence ![]() $v_i\gamma _\ell$ converging to
$v_i\gamma _\ell$ converging to ![]() $0$ for some
$0$ for some ![]() $\gamma _\ell \in \Gamma$. Using the Iwasawa decomposition
$\gamma _\ell \in \Gamma$. Using the Iwasawa decomposition ![]() $G=g_i NA K_0$, we may write
$G=g_i NA K_0$, we may write ![]() $\gamma _\ell =g_i n_\ell a_{t_\ell } k_\ell$ with
$\gamma _\ell =g_i n_\ell a_{t_\ell } k_\ell$ with ![]() $n_\ell \in N, t_\ell \in \mathbb {R}$ and
$n_\ell \in N, t_\ell \in \mathbb {R}$ and ![]() $k_\ell \in K_0$. Since
$k_\ell \in K_0$. Since
the assumption that ![]() $v_i\gamma _\ell \to 0$ implies that
$v_i\gamma _\ell \to 0$ implies that ![]() $t_\ell \to -\infty$.
$t_\ell \to -\infty$.
On the other hand, as ![]() $\xi _i\in \Lambda _{\rm bp}$,
$\xi _i\in \Lambda _{\rm bp}$, ![]() $\operatorname {Stab}_\Gamma (\xi _i)=\Gamma \cap g_i AM_0Ng_i^{-1}$ contains a parabolic element, say,
$\operatorname {Stab}_\Gamma (\xi _i)=\Gamma \cap g_i AM_0Ng_i^{-1}$ contains a parabolic element, say, ![]() $\gamma '\neq e$. Note that
$\gamma '\neq e$. Note that ![]() $n_0:=g_i^{-1} \gamma ' g_i$ is then an element of
$n_0:=g_i^{-1} \gamma ' g_i$ is then an element of ![]() $N$ and hence a unipotent element, as any parabolic element of
$N$ and hence a unipotent element, as any parabolic element of ![]() $AM_0N$ belongs to
$AM_0N$ belongs to ![]() $N$ in the group
$N$ in the group ![]() $G\simeq \operatorname {PSL}_2(\mathbb {C})$. Now observe that, as
$G\simeq \operatorname {PSL}_2(\mathbb {C})$. Now observe that, as ![]() $N$ is abelian,
$N$ is abelian,
Since ![]() $t_\ell \to -\infty$, the sequence
$t_\ell \to -\infty$, the sequence ![]() $a_{-t_{\ell }} n_0 a_{t_\ell }$ converges to
$a_{-t_{\ell }} n_0 a_{t_\ell }$ converges to ![]() $e$. Since
$e$. Since ![]() $\{k_\ell ^{-1}\}$ is a bounded sequence, it follows that, up to passing to a subsequence,
$\{k_\ell ^{-1}\}$ is a bounded sequence, it follows that, up to passing to a subsequence, ![]() $\gamma _{\ell }^{-1}\gamma ' \gamma _\ell$ is an infinite sequence converging to
$\gamma _{\ell }^{-1}\gamma ' \gamma _\ell$ is an infinite sequence converging to ![]() $e$, contradicting the discreteness of
$e$, contradicting the discreteness of ![]() $\Gamma$.
$\Gamma$.
Definition 6.3 (Height function)
Define the height function ![]() $\omega :X_0\to [2, \infty )$ by
$\omega :X_0\to [2, \infty )$ by
where
this is well-defined by Lemma 6.2.
If ![]() $\Gamma$ has no parabolic elements, we define
$\Gamma$ has no parabolic elements, we define ![]() $\omega (x)=2$ for all
$\omega (x)=2$ for all ![]() $x\in X_0$.
$x\in X_0$.
By the definition of ![]() ${\varepsilon }_X$,
${\varepsilon }_X$, ![]() $X_0$ is contained in the union of
$X_0$ is contained in the union of ![]() $X_{{\varepsilon }_X}$ and
$X_{{\varepsilon }_X}$ and ![]() $\cup _{j=1}^{\ell } \mathfrak {h}_j$ where
$\cup _{j=1}^{\ell } \mathfrak {h}_j$ where ![]() $\mathfrak {h}_j$ is a horoball based at
$\mathfrak {h}_j$ is a horoball based at ![]() $\xi _j$.
$\xi _j$.
Set ![]() $\tilde {\mathfrak {h}}_j:=g_j N{A}_{(-\infty, -T_j]} K_0$.
$\tilde {\mathfrak {h}}_j:=g_j N{A}_{(-\infty, -T_j]} K_0$.
The following is an immediate consequence of the thick–thin decomposition of ![]() $M$.
$M$.
Lemma 6.4 If ![]() $\tilde {\mathfrak {h}}_j\cap \gamma \tilde {\mathfrak {h}}_i\ne \emptyset$ for some
$\tilde {\mathfrak {h}}_j\cap \gamma \tilde {\mathfrak {h}}_i\ne \emptyset$ for some ![]() $1\le i, j\le \ell$ and
$1\le i, j\le \ell$ and ![]() $\gamma \in \Gamma$, then
$\gamma \in \Gamma$, then ![]() $i=j$,
$i=j$, ![]() $\gamma \in \operatorname {Stab}_G(\xi _i)=\operatorname {Stab}\tilde {\mathfrak {h}}_i$, and hence
$\gamma \in \operatorname {Stab}_G(\xi _i)=\operatorname {Stab}\tilde {\mathfrak {h}}_i$, and hence ![]() $\tilde {\mathfrak {h}}_j= \gamma \tilde {\mathfrak {h}}_i$.
$\tilde {\mathfrak {h}}_j= \gamma \tilde {\mathfrak {h}}_i$.
Lemma 6.5 For all ![]() $1\le i, j \le \ell$ and
$1\le i, j \le \ell$ and ![]() $\gamma \in \Gamma$ such that
$\gamma \in \Gamma$ such that ![]() $\tilde {\mathfrak {h}}_j\neq \gamma \tilde {\mathfrak {h}}_i$,
$\tilde {\mathfrak {h}}_j\neq \gamma \tilde {\mathfrak {h}}_i$,
where ![]() $\eta _0:=\min _{1\le m\le \ell } e^{-T_m}.$
$\eta _0:=\min _{1\le m\le \ell } e^{-T_m}.$
Proof. Let ![]() $q\in \tilde {\mathfrak {h}}_i$ and
$q\in \tilde {\mathfrak {h}}_i$ and ![]() $\gamma \in \Gamma$. Using
$\gamma \in \Gamma$. Using ![]() $G=g_jNAK_0$, write
$G=g_jNAK_0$, write ![]() $\gamma q=g_j ua_{s}k\in g_jNAK_0$. Then
$\gamma q=g_j ua_{s}k\in g_jNAK_0$. Then ![]() $\|v_j\gamma q\|= e^s$. Hence if
$\|v_j\gamma q\|= e^s$. Hence if ![]() $\|v_j\gamma q\|<\eta _0$, then
$\|v_j\gamma q\|<\eta _0$, then ![]() $s\le -T_j$. So
$s\le -T_j$. So ![]() $\gamma q\in \tilde {\mathfrak {h}}_j$. Therefore
$\gamma q\in \tilde {\mathfrak {h}}_j$. Therefore ![]() $\tilde {\mathfrak {h}}_j\cap \gamma \tilde {\mathfrak {h}}_i\ne \emptyset$. By Lemma 6.4,
$\tilde {\mathfrak {h}}_j\cap \gamma \tilde {\mathfrak {h}}_i\ne \emptyset$. By Lemma 6.4, ![]() $\tilde {\mathfrak {h}}_j=\gamma \tilde {\mathfrak {h}}_i$.
$\tilde {\mathfrak {h}}_j=\gamma \tilde {\mathfrak {h}}_i$.
Proposition 6.7 There is an absolute constant ![]() $\alpha \ge 2$ such that for all
$\alpha \ge 2$ such that for all ![]() $x\in X_0$,
$x\in X_0$,
Proof. Fixing ![]() $1\le j\le \ell$, it suffices to show the claim for all
$1\le j\le \ell$, it suffices to show the claim for all ![]() $x\in X_0\cap \mathfrak {h}_j$.
$x\in X_0\cap \mathfrak {h}_j$.
Let ![]() $g\in g_i u a_{-t} k \in \tilde {\mathfrak {h}}_i$ be so that
$g\in g_i u a_{-t} k \in \tilde {\mathfrak {h}}_i$ be so that ![]() $x=[g]$, where
$x=[g]$, where ![]() $ua_{-t}k \in N{ A}_{(-\infty, -T_j]} K_0$.
$ua_{-t}k \in N{ A}_{(-\infty, -T_j]} K_0$.
Note that
In view of the definition of ![]() $\omega$ and
$\omega$ and ![]() $\omega _i$, this together with Lemma 6.5 implies that
$\omega _i$, this together with Lemma 6.5 implies that
Since ![]() $\operatorname {inj}(x) \asymp e^{-t}$, this finishes proof.
$\operatorname {inj}(x) \asymp e^{-t}$, this finishes proof.
7. Markov operators
In this section we define a Markov operator ![]() ${\mathsf {A}}_t$ and prove Proposition 7.5 which relates the average
${\mathsf {A}}_t$ and prove Proposition 7.5 which relates the average ![]() $m_Y(F)$ of a locally bounded, log-continuous, Borel function
$m_Y(F)$ of a locally bounded, log-continuous, Borel function ![]() $F$ on
$F$ on ![]() $Y_0$ with a super-harmonic type inequality for
$Y_0$ with a super-harmonic type inequality for ![]() ${\mathsf {A}}_t F$. This proposition will serve as a main tool in our approach to prove Theorem 1.5.
${\mathsf {A}}_t F$. This proposition will serve as a main tool in our approach to prove Theorem 1.5.
Fix a closed non-elementary ![]() $H$-orbit
$H$-orbit ![]() $Y$ in
$Y$ in ![]() $X$.
$X$.
Bowen–Margulis–Sullivan measure  $m_Y$
$m_Y$
We denote by ![]() $m_Y$ the Bowen–Margulis–Sullivan probability measure on
$m_Y$ the Bowen–Margulis–Sullivan probability measure on ![]() $\Delta _Y\backslash H=\operatorname {T}^1(S_Y)$, which is the unique probability measure of maximal entropy (that is
$\Delta _Y\backslash H=\operatorname {T}^1(S_Y)$, which is the unique probability measure of maximal entropy (that is ![]() $\delta (Y))$ for the geodesic flow. We will also use the same notation
$\delta (Y))$ for the geodesic flow. We will also use the same notation ![]() $m_Y$ to denote the push-forward of the measure to
$m_Y$ to denote the push-forward of the measure to ![]() $Y$ via the map
$Y$ via the map ![]() $\operatorname {Stab}_H(y_0)\backslash H\to Y$ given by
$\operatorname {Stab}_H(y_0)\backslash H\to Y$ given by ![]() $[h]\to y_0h$. Considered as a measure on
$[h]\to y_0h$. Considered as a measure on ![]() $Y$,
$Y$, ![]() $m_Y$ is well defined, independent of the choice of
$m_Y$ is well defined, independent of the choice of ![]() $y_0\in Y$.
$y_0\in Y$.
Recall the definition of ![]() $Y_0$ in (4.4); note that
$Y_0$ in (4.4); note that ![]() $Y_0=\operatorname {supp}m_Y$. In the following, all of our Borel functions are assumed to be defined everywhere in their domains. By a locally bounded function, we mean a function which is bounded on every compact subset.
$Y_0=\operatorname {supp}m_Y$. In the following, all of our Borel functions are assumed to be defined everywhere in their domains. By a locally bounded function, we mean a function which is bounded on every compact subset.
Definition 7.1 (Markov operator)
Let ![]() $t\in \mathbb {R}$ and
$t\in \mathbb {R}$ and ![]() $\rho >0$. For a locally bounded Borel function
$\rho >0$. For a locally bounded Borel function ![]() $\psi :Y_0\to \mathbb {R}$, we define
$\psi :Y_0\to \mathbb {R}$, we define
We set ![]() ${\mathsf {A}}_t:={\mathsf {A}}_{t, 1}$.
${\mathsf {A}}_t:={\mathsf {A}}_{t, 1}$.
Note that ![]() ${\mathsf {A}}_{t, \rho } \psi$ is a locally bounded Borel function on
${\mathsf {A}}_{t, \rho } \psi$ is a locally bounded Borel function on ![]() $Y_0$. Although
$Y_0$. Although ![]() $\lim _{n\to \infty }\mathsf {A}_{nt} (\psi )= m_Y(\psi )$ for any
$\lim _{n\to \infty }\mathsf {A}_{nt} (\psi )= m_Y(\psi )$ for any ![]() $\psi \in C_c(Y_0)$ and any
$\psi \in C_c(Y_0)$ and any ![]() $t>0$ [Reference Oh and ShahOS13], the Margulis function
$t>0$ [Reference Oh and ShahOS13], the Margulis function ![]() $F$ we will be constructing is not a continuous function on
$F$ we will be constructing is not a continuous function on ![]() $Y_0$, and hence we cannot use such an equidistribution statement to control
$Y_0$, and hence we cannot use such an equidistribution statement to control ![]() $m_Y(F)$. We will use the following lemma instead.
$m_Y(F)$. We will use the following lemma instead.
Lemma 7.3 Let ![]() $F:Y_0\to [2,\infty )$ be a locally bounded Borel function. Assume that there exist some
$F:Y_0\to [2,\infty )$ be a locally bounded Borel function. Assume that there exist some ![]() $t>0$ and
$t>0$ and ![]() $D>0$ such that
$D>0$ such that
Then
Proof. For every ![]() $k\ge 2$, let
$k\ge 2$, let ![]() $F_k:Y_0\to [2, \infty )$ be given by
$F_k:Y_0\to [2, \infty )$ be given by
As ![]() $F_k$ is bounded, it belongs to
$F_k$ is bounded, it belongs to ![]() $L^1(Y_0, m_Y)$. Since the action of
$L^1(Y_0, m_Y)$. Since the action of ![]() $A$ is mixing for
$A$ is mixing for ![]() $m_Y$ by the work of Babillot [Reference BabillotBab02], we have
$m_Y$ by the work of Babillot [Reference BabillotBab02], we have ![]() $m_Y$ is
$m_Y$ is ![]() $a_t$-ergodic for each
$a_t$-ergodic for each ![]() $t\ne 0$. Hence, by the Birkhoff ergodic theorem, for
$t\ne 0$. Hence, by the Birkhoff ergodic theorem, for ![]() $m_Y$ a.e.
$m_Y$ a.e. ![]() $y\in Y_0$, we have
$y\in Y_0$, we have
 \[ \lim_{N\to \infty} \frac{1}{N}\sum_{n=1}^N F_k(ya_{nt}) =\int F_k\,dm_Y. \]
\[ \lim_{N\to \infty} \frac{1}{N}\sum_{n=1}^N F_k(ya_{nt}) =\int F_k\,dm_Y. \]
Therefore, using Egorov's theorem, for every ![]() ${\varepsilon }>0$, there exist
${\varepsilon }>0$, there exist ![]() $N_{\varepsilon }>1$ and a measurable subset
$N_{\varepsilon }>1$ and a measurable subset ![]() $Y_{\varepsilon }'\subset Y_0$ with
$Y_{\varepsilon }'\subset Y_0$ with ![]() $m_Y(Y_{\varepsilon }')>1-{\varepsilon }^2$ such that for every
$m_Y(Y_{\varepsilon }')>1-{\varepsilon }^2$ such that for every ![]() $y\in Y_{\varepsilon }'$ and all
$y\in Y_{\varepsilon }'$ and all ![]() $N>N_{\varepsilon }$, we have
$N>N_{\varepsilon }$, we have
 \[ \frac{1}{N}\sum_{n=1}^N F_k(ya_{nt})>\frac{1}{2}\int F_k\,dm_Y. \]
\[ \frac{1}{N}\sum_{n=1}^N F_k(ya_{nt})>\frac{1}{2}\int F_k\,dm_Y. \]
Now by the maximal ergodic theorem [Reference LindenstraussLin06, Appendix A.1], if ![]() ${\varepsilon }$ is small enough, there exists a measurable subset
${\varepsilon }$ is small enough, there exists a measurable subset ![]() $Y_{\varepsilon }\subset Y'_{\varepsilon }$ with
$Y_{\varepsilon }\subset Y'_{\varepsilon }$ with ![]() $m(Y_{\varepsilon })>1-{\varepsilon }$ so that for all
$m(Y_{\varepsilon })>1-{\varepsilon }$ so that for all ![]() $y\in Y_{\varepsilon }$, we have
$y\in Y_{\varepsilon }$, we have
Altogether, if ![]() $y\in Y_{\varepsilon }$ and
$y\in Y_{\varepsilon }$ and ![]() $N>N_{\varepsilon }$, we have
$N>N_{\varepsilon }$, we have
 \[ \frac 1 N \sum_{n=1}^N {\mathsf{A}}_{nt} F_k(y) =\frac{1}{\mu_y([-1,1])}\int_{-1}^{1}\frac{1}{N}\sum_{n=1}^N F_k(yu_ra_{nt}) \,d\mu_y(r)>{\frac{1}{4}}\int F_k\,dm_Y. \]
\[ \frac 1 N \sum_{n=1}^N {\mathsf{A}}_{nt} F_k(y) =\frac{1}{\mu_y([-1,1])}\int_{-1}^{1}\frac{1}{N}\sum_{n=1}^N F_k(yu_ra_{nt}) \,d\mu_y(r)>{\frac{1}{4}}\int F_k\,dm_Y. \]
Fix ![]() $y\in Y_{\varepsilon }$. By the hypothesis (7.4), there exists
$y\in Y_{\varepsilon }$. By the hypothesis (7.4), there exists ![]() $n_0=n_0(y)$ such that for all
$n_0=n_0(y)$ such that for all ![]() $n\ge n_0$, we have
$n\ge n_0$, we have
Therefore, we deduce that for all sufficiently large ![]() $N\gg 1$,
$N\gg 1$,
 \[ \frac{1}{4}\int F_k\,dm_Y \le \frac{1}{N} \bigg(\sum_{n=1}^{n_0} {\mathsf{A}}_{nt} F_k(y) +\sum_{n=n_0+1}^N {\mathsf{A}}_{nt} F_k (y) \bigg) \le \frac{k n_0}N +\frac{ 2D(N-n_0)}{N}. \]
\[ \frac{1}{4}\int F_k\,dm_Y \le \frac{1}{N} \bigg(\sum_{n=1}^{n_0} {\mathsf{A}}_{nt} F_k(y) +\sum_{n=n_0+1}^N {\mathsf{A}}_{nt} F_k (y) \bigg) \le \frac{k n_0}N +\frac{ 2D(N-n_0)}{N}. \]
By sending ![]() $N\to \infty$, we get that for all
$N\to \infty$, we get that for all ![]() $k>2$,
$k>2$,
Since ![]() $\{F_k:k=3,4,..\}$ is an increasing sequence of positive functions converging to
$\{F_k:k=3,4,..\}$ is an increasing sequence of positive functions converging to ![]() $F$ point-wise, the monotone convergence theorem implies
$F$ point-wise, the monotone convergence theorem implies
as we claimed.
We remark that in [Reference Eskin, Margulis and MozesEMM98], the Markov operator ![]() $\mathsf {A}_t$ was defined using the integral over the translates
$\mathsf {A}_t$ was defined using the integral over the translates ![]() $\operatorname {SO}(2) a_t$, whereas we use the integral over the translates
$\operatorname {SO}(2) a_t$, whereas we use the integral over the translates ![]() $U_{[-\rho,\rho ]}a_t$ of a horocyclic piece. The proof of the following proposition, which is an analogue of [Reference Eskin, Margulis and MozesEMM98, § 5.3], is the main reason for our digression from their definition, as the handling of the PS-measure on
$U_{[-\rho,\rho ]}a_t$ of a horocyclic piece. The proof of the following proposition, which is an analogue of [Reference Eskin, Margulis and MozesEMM98, § 5.3], is the main reason for our digression from their definition, as the handling of the PS-measure on ![]() $U$ is more manageable than that of the PS-measure on
$U$ is more manageable than that of the PS-measure on ![]() $\operatorname {SO}(2)$ in performing change of variables.
$\operatorname {SO}(2)$ in performing change of variables.
Proposition 7.5 Let ![]() $F:Y_0\to [2,\infty )$ be a locally bounded Borel function satisfying the following properties.
$F:Y_0\to [2,\infty )$ be a locally bounded Borel function satisfying the following properties.
(a) There exists
 $\sigma \ge 2$ such that for all
$\sigma \ge 2$ such that for all  $h\in B_H(2)$ and
$h\in B_H(2)$ and  $y\in Y_0$,
$y\in Y_0$,
 \[ \sigma^{-1}F(y)\leq F(yh)\leq \sigma F(y). \]
\[ \sigma^{-1}F(y)\leq F(yh)\leq \sigma F(y). \]
(b) There exist
 $t\geq 2$ and
$t\geq 2$ and  $D_0>0$ such that for all
$D_0>0$ such that for all  $y\in Y_0$ and
$y\in Y_0$ and  $1\le \rho \le 2$,
where
$1\le \rho \le 2$,
where \[ {\mathsf{A}}_{t,\rho}F(y)\leq\frac{1}{8 \sigma \mathsf{p}_Y^{\delta_Y}} \cdot F(y)+D_0, \]
\[ {\mathsf{A}}_{t,\rho}F(y)\leq\frac{1}{8 \sigma \mathsf{p}_Y^{\delta_Y}} \cdot F(y)+D_0, \]
 $\mathsf {p}_Y$ is as in (4.6).
$\mathsf {p}_Y$ is as in (4.6).
Then
In view of Lemma 7.3, Proposition 7.5 is an immediate consequence of the following.
Proposition 7.6 Let ![]() $F$ be as in Proposition 7.5. Then for all
$F$ be as in Proposition 7.5. Then for all ![]() $y\in Y_0$ and
$y\in Y_0$ and ![]() $n\geq 1$, we have
$n\geq 1$, we have
Proof. The main step of the proof is the following estimate.
Claim For any ![]() $1\leq \rho \leq \frac 32$,
$1\leq \rho \leq \frac 32$, ![]() $y\in Y_0$ and
$y\in Y_0$ and ![]() $n\in \mathbb {N}$, we have
$n\in \mathbb {N}$, we have
where ![]() $\hat D:=4 D_0 \mathsf {p}_Y^{\delta _Y}$; recall that
$\hat D:=4 D_0 \mathsf {p}_Y^{\delta _Y}$; recall that ![]() $e^{-nt}\leq 1/2$.
$e^{-nt}\leq 1/2$.
Let us first assume this claim and prove the proposition. We observe:
•
 $\sum _{j\ge 1} e^{-jt}\leq 1/2$ (as
$\sum _{j\ge 1} e^{-jt}\leq 1/2$ (as  $t\ge 2$);
$t\ge 2$);•
 $({8 \sigma \mathsf {p}_Y^{\delta _Y}} )^{-1} \le 1/2$; and
$({8 \sigma \mathsf {p}_Y^{\delta _Y}} )^{-1} \le 1/2$; and•
 $D_0\le \hat D$.
$D_0\le \hat D$.
Using the assumption (b) of Proposition 7.5 with ![]() $\rho _n=1+\sum _{j=1}^{n-1} e^{-jt}$ (
$\rho _n=1+\sum _{j=1}^{n-1} e^{-jt}$ (![]() $n\geq 2$), we deduce that for any
$n\geq 2$), we deduce that for any ![]() $n\geq 2$,
$n\geq 2$,
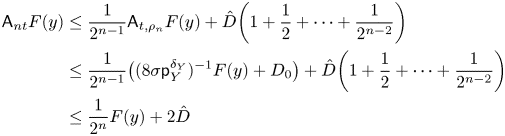 \begin{align} {\mathsf{A}}_{nt} F(y)& \leq \frac{1}{2^{n-1}} {\mathsf{A}}_{t, \rho_n}F(y)+\hat D\bigg(1+ \frac 12 +\cdots+ \frac 1{2^{n-2}}\bigg) \nonumber\\ &\leq \frac 1{2^{n-1}} \big((8 \sigma \mathsf{p}_Y^{\delta_Y})^{-1} F(y)+D_0\big)+\hat D\bigg(1+\frac 1{2} +\cdots+\frac 1{2^{n-2}}\bigg)\nonumber\\ &\leq \frac 1{2^{n}} F(y)+2\hat{D} \end{align}
\begin{align} {\mathsf{A}}_{nt} F(y)& \leq \frac{1}{2^{n-1}} {\mathsf{A}}_{t, \rho_n}F(y)+\hat D\bigg(1+ \frac 12 +\cdots+ \frac 1{2^{n-2}}\bigg) \nonumber\\ &\leq \frac 1{2^{n-1}} \big((8 \sigma \mathsf{p}_Y^{\delta_Y})^{-1} F(y)+D_0\big)+\hat D\bigg(1+\frac 1{2} +\cdots+\frac 1{2^{n-2}}\bigg)\nonumber\\ &\leq \frac 1{2^{n}} F(y)+2\hat{D} \end{align}which establishes the proposition.
We now prove the claim (7.8). For ![]() $y\in Y_0$ and
$y\in Y_0$ and ![]() $\rho >0$, set
$\rho >0$, set
To ease the notation, we prove (7.8) with ![]() $\rho =1$; the proof in general is similar. By assumption (a) and (b) of Proposition 7.5, we have
$\rho =1$; the proof in general is similar. By assumption (a) and (b) of Proposition 7.5, we have
where ![]() $c_0=({8 \sigma \mathsf {p}_Y^{\delta _Y}})^{-1}$.
$c_0=({8 \sigma \mathsf {p}_Y^{\delta _Y}})^{-1}$.
Set ![]() $\rho _n:=e^{-nt}$. Let
$\rho _n:=e^{-nt}$. Let ![]() $\{[r_j-\rho _n, r_j+\rho _n]: j\in J\}$ be a covering of
$\{[r_j-\rho _n, r_j+\rho _n]: j\in J\}$ be a covering of
with ![]() $r_j\in [-1,1]\cap {\rm supp}(\mu _{y})$ and with multiplicity bounded by
$r_j\in [-1,1]\cap {\rm supp}(\mu _{y})$ and with multiplicity bounded by ![]() $2$. For each
$2$. For each ![]() $j\in J$, let
$j\in J$, let ![]() $z_j:=yu_{r_j}$. Then
$z_j:=yu_{r_j}$. Then
Moreover, we get
 \begin{align} {\mathsf{A}}_{(n+1)t} F(y)&=\frac{1}{b_y}\int_{-1}^1 F(yu_{r}a_{(n+1)t})\,d\mu_{y}{}(r)\nonumber\\ &\leq\frac{1}{b_y}\sum_j\int_{-\rho_n}^{\rho_n}F(z_ju_{r}a_{(n+1)t})\,d\mu_{{z_j}}{}(r)\nonumber\\ &=\frac{1}{b_y}\sum_j\int_{-\rho_n}^{\rho_n}F(z_ja_{nt}u_{re^{nt}}a_t)\,d\mu_{z_j}{}(r). \end{align}
\begin{align} {\mathsf{A}}_{(n+1)t} F(y)&=\frac{1}{b_y}\int_{-1}^1 F(yu_{r}a_{(n+1)t})\,d\mu_{y}{}(r)\nonumber\\ &\leq\frac{1}{b_y}\sum_j\int_{-\rho_n}^{\rho_n}F(z_ju_{r}a_{(n+1)t})\,d\mu_{{z_j}}{}(r)\nonumber\\ &=\frac{1}{b_y}\sum_j\int_{-\rho_n}^{\rho_n}F(z_ja_{nt}u_{re^{nt}}a_t)\,d\mu_{z_j}{}(r). \end{align}
We now make the change of variables ![]() $s=re^{nt}$. In view of (7.12), we have
$s=re^{nt}$. In view of (7.12), we have
 \[ {\mathsf{A}}_{(n+1)t} F(y)\leq\frac{1}{b_y}\sum_j\frac{b_{z_j}(\rho_n)}{b_{z_ja_{nt}}}\int_{-1}^1F(z_ja_{nt}u_{s}a_t)\,d\mu_{z_ja_{nt}}{}(s). \]
\[ {\mathsf{A}}_{(n+1)t} F(y)\leq\frac{1}{b_y}\sum_j\frac{b_{z_j}(\rho_n)}{b_{z_ja_{nt}}}\int_{-1}^1F(z_ja_{nt}u_{s}a_t)\,d\mu_{z_ja_{nt}}{}(s). \]
Applying (7.10) with the base point ![]() $z_ja_{nt}$, we get from the above that
$z_ja_{nt}$, we get from the above that
 \begin{align} {\mathsf{A}}_{(n+1)t} F(y)&\leq\frac{1}{b_y}\sum_j\frac{b_{z_j}(\rho_n)c_0\sigma}{b_{z_ja_{nt}}}\int_{-1}^1 F(z_ja_{nt}u_{s})\,d\mu_{z_ja_{nt}}{}(s)\nonumber\\ &\quad +\frac{1}{b_y}\sum_jb_{z_j}(\rho_n)D_0. \end{align}
\begin{align} {\mathsf{A}}_{(n+1)t} F(y)&\leq\frac{1}{b_y}\sum_j\frac{b_{z_j}(\rho_n)c_0\sigma}{b_{z_ja_{nt}}}\int_{-1}^1 F(z_ja_{nt}u_{s})\,d\mu_{z_ja_{nt}}{}(s)\nonumber\\ &\quad +\frac{1}{b_y}\sum_jb_{z_j}(\rho_n)D_0. \end{align}
By (7.11), we have ![]() $({1}/{b_y})\sum _jb_{z_j}(\rho _n)D_0\leq \hat D.$
$({1}/{b_y})\sum _jb_{z_j}(\rho _n)D_0\leq \hat D.$
Therefore, reversing the change of variable, i.e. now letting ![]() $r=e^{-nt}s$, we get from (7.13) the following:
$r=e^{-nt}s$, we get from (7.13) the following:
 \begin{align*} {\mathsf{A}}_{(n+1)t} F(y)&\leq \frac{1}{b_y}\sum_j c_0\sigma\int_{-\rho_n}^{\rho_n} F(z_ju_{r}a_{nt}) \,d\mu_{z_j}{}(r)+\hat{D}\\ &\leq \frac{2c_0\sigma}{b_y}\int_{-(1+\rho_n)}^{1+\rho_n} F(yu_{r}a_{nt}) \,d\mu_{y}{}(r)+\hat{D}\\ &=\frac{2c_0\sigma b_y(1+\rho_n)}{b_y } {\mathsf{A}}_{nt, 1+\rho_n}F(y) +\hat{D}. \end{align*}
\begin{align*} {\mathsf{A}}_{(n+1)t} F(y)&\leq \frac{1}{b_y}\sum_j c_0\sigma\int_{-\rho_n}^{\rho_n} F(z_ju_{r}a_{nt}) \,d\mu_{z_j}{}(r)+\hat{D}\\ &\leq \frac{2c_0\sigma}{b_y}\int_{-(1+\rho_n)}^{1+\rho_n} F(yu_{r}a_{nt}) \,d\mu_{y}{}(r)+\hat{D}\\ &=\frac{2c_0\sigma b_y(1+\rho_n)}{b_y } {\mathsf{A}}_{nt, 1+\rho_n}F(y) +\hat{D}. \end{align*}
Since
we get
The proof is complete.
8. Return lemma and number of nearby sheets
We fix closed non-elementary ![]() $H$-orbits
$H$-orbits ![]() $Y$ and
$Y$ and ![]() $Z$ in
$Z$ in ![]() $X$. Since
$X$. Since ![]() $Z$ is closed, a fixed ball around
$Z$ is closed, a fixed ball around ![]() $y\in Y_0$ intersects only finitely many sheets of
$y\in Y_0$ intersects only finitely many sheets of ![]() $Z$ (see Figure 2). The aim of this section is to show that the number of sheets of
$Z$ (see Figure 2). The aim of this section is to show that the number of sheets of ![]() $Z$ in
$Z$ in ![]() $B(y, \operatorname {inj} (y))$ is controlled by the tight area of
$B(y, \operatorname {inj} (y))$ is controlled by the tight area of ![]() $S_Z$ with a multiplicative constant depending on
$S_Z$ with a multiplicative constant depending on ![]() $\mathsf {p}_Y$ and
$\mathsf {p}_Y$ and ![]() $\delta _Y$.
$\delta _Y$.
The main ingredient is a return lemma which says that for any ![]() $y\in Y_0$, there exists some point in
$y\in Y_0$, there exists some point in ![]() $\{yu_r\in Y_0: r\in [-1,1]\}$ whose minimum return time to a fixed compact subset under the geodesic flow is comparable to
$\{yu_r\in Y_0: r\in [-1,1]\}$ whose minimum return time to a fixed compact subset under the geodesic flow is comparable to ![]() $\log (\omega (y))$ (see Lemma 8.4).
$\log (\omega (y))$ (see Lemma 8.4).
Return lemma
We use the notation of § 6.
Recall that ![]() ${\rm Lie}(G)=i\mathfrak {sl}_2(\mathbb {R})\oplus \mathfrak {sl}_2(\mathbb {R})$. We define a norm
${\rm Lie}(G)=i\mathfrak {sl}_2(\mathbb {R})\oplus \mathfrak {sl}_2(\mathbb {R})$. We define a norm ![]() $\|\cdot \|$ on
$\|\cdot \|$ on ![]() $\operatorname {Lie}(G)$ using an inner product with respect to which
$\operatorname {Lie}(G)$ using an inner product with respect to which ![]() $\mathfrak {sl}_2(\mathbb {R})$ and
$\mathfrak {sl}_2(\mathbb {R})$ and ![]() $i\mathfrak {sl}_2(\mathbb {R})$ are orthogonal to each other. Given a vector
$i\mathfrak {sl}_2(\mathbb {R})$ are orthogonal to each other. Given a vector ![]() $w\in {\rm Lie}(G)$, we write
$w\in {\rm Lie}(G)$, we write
Since the exponential map ![]() ${\rm Lie} (G) \to G$ defines a local diffeomorphism, there exists an absolute constant
${\rm Lie} (G) \to G$ defines a local diffeomorphism, there exists an absolute constant ![]() $c_1\ge 2$ satisfying the following two properties.
$c_1\ge 2$ satisfying the following two properties.
(1) For all
 $x\in X$, and all
$x\in X$, and all  $w=i{\rm Im}(w)+{\rm Re}(w)\in \operatorname {Lie}(G)$ with
$w=i{\rm Im}(w)+{\rm Re}(w)\in \operatorname {Lie}(G)$ with  $\|w\| \le \max (1, {\varepsilon }_X)$,
(8.1)
$\|w\| \le \max (1, {\varepsilon }_X)$,
(8.1) \begin{equation} c_1^{-1}\|w\|\leq d(x,x\exp(i {\rm Im}(w))\exp({\rm Re}(w)))\leq c_1\|w\|. \end{equation}
\begin{equation} c_1^{-1}\|w\|\leq d(x,x\exp(i {\rm Im}(w))\exp({\rm Re}(w)))\leq c_1\|w\|. \end{equation}(2) If
 $d(x,x')\leq {\varepsilon }_X/c_1$, then
$d(x,x')\leq {\varepsilon }_X/c_1$, then  $x'=x\exp (i {\rm Im}(w))\exp ({\rm Re}(w))$ for some
$x'=x\exp (i {\rm Im}(w))\exp ({\rm Re}(w))$ for some  $w\in {\rm Lie}(G)$.
$w\in {\rm Lie}(G)$.
We choose an absolute constant ![]() $d_X\ge 24$ so that
$d_X\ge 24$ so that
Let ![]() $D_1:=D_1(Y)$ be given by
$D_1:=D_1(Y)$ be given by
where ![]() $\kappa$ is defined by
$\kappa$ is defined by ![]() $\hat {b}_0 \mathsf {p}_Y^{\delta _Y} \kappa ^{\delta _Y/2}=1/2$,
$\hat {b}_0 \mathsf {p}_Y^{\delta _Y} \kappa ^{\delta _Y/2}=1/2$, ![]() $0<\eta _0 <1$ is as in (6.6),
$0<\eta _0 <1$ is as in (6.6), ![]() $\alpha \ge 1$ is as in (6.8), and
$\alpha \ge 1$ is as in (6.8), and ![]() $c_1$ is as in (8.1). We note that by increasing
$c_1$ is as in (8.1). We note that by increasing ![]() $\hat {b}_0$ if necessary, we may and will assume that
$\hat {b}_0$ if necessary, we may and will assume that ![]() $\kappa \in (0,1)$. Moreover, we put
$\kappa \in (0,1)$. Moreover, we put ![]() $\eta _0=\frac 12$ when
$\eta _0=\frac 12$ when ![]() $Y$ is convex cocompact.
$Y$ is convex cocompact.
Define
Note that ![]() $X_{{\varepsilon }_X}\cap Y_0 \subset \mathcal {K}_Y$.
$X_{{\varepsilon }_X}\cap Y_0 \subset \mathcal {K}_Y$.
The choices of the above parameters are motivated by our applications in the following lemmas. Indeed the choice of ![]() $\kappa$ is used in (8.6). The multiplicative parameter
$\kappa$ is used in (8.6). The multiplicative parameter ![]() $c_1\alpha$, which features in the definitions of
$c_1\alpha$, which features in the definitions of ![]() ${D_1}$ and
${D_1}$ and ![]() $\mathcal {K}_Y$, is tailored so that we may utilize Lemma 8.10 in the proof of Lemma 8.13.
$\mathcal {K}_Y$, is tailored so that we may utilize Lemma 8.10 in the proof of Lemma 8.13.
Lemma 8.4 (Return lemma)
For every ![]() $y\in Y_0$, there exists some
$y\in Y_0$, there exists some ![]() $|r|\leq 1$ so that
$|r|\leq 1$ so that ![]() $yu_ra_{-t}\in \mathcal {K}_Y$ where
$yu_ra_{-t}\in \mathcal {K}_Y$ where ![]() $t=\log (\eta _0\omega (y)/6)$.
$t=\log (\eta _0\omega (y)/6)$.
Proof. Let ![]() $y\in Y_0-\mathcal {K}_Y$. By the definition of
$y\in Y_0-\mathcal {K}_Y$. By the definition of ![]() $\omega$, there exist
$\omega$, there exist ![]() $1\le i\le \ell$ and
$1\le i\le \ell$ and ![]() $g\in \tilde {\mathfrak {h}}_i$ so that
$g\in \tilde {\mathfrak {h}}_i$ so that ![]() $y=[g]$ and
$y=[g]$ and
see § 6 for the notation. Set ![]() $v:= v_i g$. Then
$v:= v_i g$. Then
Let us write ![]() $v=w+se_3$ where
$v=w+se_3$ where ![]() $w\in V$ and
$w\in V$ and ![]() $s\in \mathbb {R}$. Recall from Lemma 5.12 that there exists
$s\in \mathbb {R}$. Recall from Lemma 5.12 that there exists ![]() $b_1>1$ so that
$b_1>1$ so that
Let ![]() $\kappa >0$ be as used in (8.2). Then (5.5) implies that
$\kappa >0$ be as used in (8.2). Then (5.5) implies that
Therefore, there exists ![]() $r\in {\rm supp}(\mu _y)\cap \big ([-1,1]- D^+( {w}/{\|w\|},\kappa )\big )$. This means that
$r\in {\rm supp}(\mu _y)\cap \big ([-1,1]- D^+( {w}/{\|w\|},\kappa )\big )$. This means that ![]() $yu_r\in Y_0$, moreover, we have, using (8.5),
$yu_r\in Y_0$, moreover, we have, using (8.5),
Set ![]() $t:=\log (\eta _0 \omega (y)/ 6)$. Then
$t:=\log (\eta _0 \omega (y)/ 6)$. Then
 \begin{align*} \kappa b_1^{-1}{\|v\|} \cdot\frac{ \eta_0 \omega(y)}{6} &= \kappa b_1^{-1}{\|v\|} e^t \le \|p^+(vu_r)a_t\| \\ &\le \| v u_{r} a_t\|\le \|vu_r\|e^t\le 2\|v\| \cdot\frac{ \eta_0 \omega(y)}{6}, \end{align*}
\begin{align*} \kappa b_1^{-1}{\|v\|} \cdot\frac{ \eta_0 \omega(y)}{6} &= \kappa b_1^{-1}{\|v\|} e^t \le \|p^+(vu_r)a_t\| \\ &\le \| v u_{r} a_t\|\le \|vu_r\|e^t\le 2\|v\| \cdot\frac{ \eta_0 \omega(y)}{6}, \end{align*}
where we use ![]() $\|vu_r\|\leq 2\|v\|$ in the last inequality.
$\|vu_r\|\leq 2\|v\|$ in the last inequality.
Hence, using the fact that ![]() $\omega (y)=\|v\|^{-1}$,
$\omega (y)=\|v\|^{-1}$,
This in particular implies that ![]() $gu_ra_t\in \tilde {\mathfrak {h}}_i$. By Lemma 6.5, whenever
$gu_ra_t\in \tilde {\mathfrak {h}}_i$. By Lemma 6.5, whenever ![]() $\gamma \in \Gamma$ and
$\gamma \in \Gamma$ and ![]() $1\leq j\leq \ell$ satisfy that
$1\leq j\leq \ell$ satisfy that ![]() $\tilde {\mathfrak {h}}_j\neq \gamma \tilde {\mathfrak {h}}_i$, we have
$\tilde {\mathfrak {h}}_j\neq \gamma \tilde {\mathfrak {h}}_i$, we have
note that ![]() $i=j$ is allowed.
$i=j$ is allowed.
This and the above upper bound thus imply
Therefore,
proving the claim.
Number of nearby sheets
Recalling that ![]() $\mathfrak {sl}_2(\mathbb {C})=\mathfrak {sl}_2(\mathbb {R}) \oplus i\mathfrak {sl}_2(\mathbb {R})$, we set
$\mathfrak {sl}_2(\mathbb {C})=\mathfrak {sl}_2(\mathbb {R}) \oplus i\mathfrak {sl}_2(\mathbb {R})$, we set ![]() $V=i\mathfrak {sl}_2(\mathbb {R})$ and consider the action of
$V=i\mathfrak {sl}_2(\mathbb {R})$ and consider the action of ![]() $H$ on
$H$ on ![]() $V$ via the adjoint representation; so
$V$ via the adjoint representation; so ![]() $v\cdot h= h^{-1} v h$ for
$v\cdot h= h^{-1} v h$ for ![]() $v\in V$ and
$v\in V$ and ![]() $h\in H$. We use the relation
$h\in H$. We use the relation ![]() $g (\exp v) h= gh \exp (v\cdot h)$ which is valid for all
$g (\exp v) h= gh \exp (v\cdot h)$ which is valid for all ![]() $g\in G, v\in V, h\in H$.
$g\in G, v\in V, h\in H$.
If ![]() $D\ge \alpha /2$ for
$D\ge \alpha /2$ for ![]() $\alpha$ as in Proposition 6.7, then
$\alpha$ as in Proposition 6.7, then ![]() $D^{-1}\omega (y)^{-1}\le \tfrac 12 \operatorname {inj} (y)$.
$D^{-1}\omega (y)^{-1}\le \tfrac 12 \operatorname {inj} (y)$.
Definition 8.7 For ![]() $y\in Y_0$ and
$y\in Y_0$ and ![]() $D\ge \alpha /2$, we define
$D\ge \alpha /2$, we define
Since ![]() $V$ is the orthogonal complement to
$V$ is the orthogonal complement to ![]() ${\rm Lie} (H)$, the set
${\rm Lie} (H)$, the set ![]() $I_Z(y, D)$ can be understood as the number of sheets of
$I_Z(y, D)$ can be understood as the number of sheets of ![]() $Z$ in the ball around
$Z$ in the ball around ![]() $y$ of radius
$y$ of radius ![]() $D^{-1}\omega (y)^{-1}$.
$D^{-1}\omega (y)^{-1}$.
It turns out that ![]() $\# I_Z(y, D)$ can be controlled in terms of the tight area of
$\# I_Z(y, D)$ can be controlled in terms of the tight area of ![]() $S_Z$, uniformly over all
$S_Z$, uniformly over all ![]() $y\in Y_0$ for an appropriate
$y\in Y_0$ for an appropriate ![]() $D>1$.
$D>1$.
Notation 8.9 We set
Theorem 3.3 shows that ![]() $1\ll \tau _Z<\infty$ where the implied constant depends only on
$1\ll \tau _Z<\infty$ where the implied constant depends only on ![]() $M$.
$M$.
We begin with the following lemma.
Lemma 8.10 With ![]() $c_1\ge 2$ and
$c_1\ge 2$ and ![]() $\alpha \ge 2$ given respectively in (8.1) and (6.7), we have that for all
$\alpha \ge 2$ given respectively in (8.1) and (6.7), we have that for all ![]() $y\in Y_0$,
$y\in Y_0$,
Proof. Let ![]() $c_1\ge 1$ and
$c_1\ge 1$ and ![]() $\alpha$ be the absolute constants given in (8.1) and (6.7) respectively. It follows that for any
$\alpha$ be the absolute constants given in (8.1) and (6.7) respectively. It follows that for any ![]() $y\in Y_0$ and
$y\in Y_0$ and ![]() $v\in I_Z(y,\alpha )$,
$v\in I_Z(y,\alpha )$,
It follows that for each ![]() $v\in I_Z(y, c_1\alpha )$,
$v\in I_Z(y, c_1\alpha )$, ![]() $\operatorname {inj}(y\exp v)\ge {\operatorname {inj} (y)}/{2}$. Hence the balls
$\operatorname {inj}(y\exp v)\ge {\operatorname {inj} (y)}/{2}$. Hence the balls ![]() $B_Z(y\exp v, {\operatorname {inj}(y)}/{2})$,
$B_Z(y\exp v, {\operatorname {inj}(y)}/{2})$, ![]() $v\in I_Z(y,c_1 \alpha )$ are disjoint from each other, and hence
$v\in I_Z(y,c_1 \alpha )$ are disjoint from each other, and hence
On the other hand, if we set ![]() $\rho _y:=\min \{1, \operatorname {inj}(y)/2\}$, then
$\rho _y:=\min \{1, \operatorname {inj}(y)/2\}$, then
Therefore
we have used that ![]() $2\pi (\cosh r -1)\ge r^3$ for all
$2\pi (\cosh r -1)\ge r^3$ for all ![]() $r>0$ and Proposition 6.7 respectively in the last two estimates.
$r>0$ and Proposition 6.7 respectively in the last two estimates.
Let ![]() $D_1$ be as in (8.2). By the choice of
$D_1$ be as in (8.2). By the choice of ![]() $\kappa$, we have
$\kappa$, we have ![]() $D_1\ll \mathsf {p}_Y^2$ (see the discussion following (8.2)).
$D_1\ll \mathsf {p}_Y^2$ (see the discussion following (8.2)).
Lemma 8.13 (Number of sheets)
For ![]() $D_1=D_1(Y)\ll \mathsf {p}_Y^2$ as in (8.2), we have
$D_1=D_1(Y)\ll \mathsf {p}_Y^2$ as in (8.2), we have
where ![]() $c_0\geq 2$ is an absolute constant.
$c_0\geq 2$ is an absolute constant.
Proof. Let ![]() $\mathcal {K}_Y$ be as in (8.3):
$\mathcal {K}_Y$ be as in (8.3):
If ![]() $y\in \mathcal {K}_Y$, then, by Lemma 8.10,
$y\in \mathcal {K}_Y$, then, by Lemma 8.10,
Now suppose that ![]() $y\in Y_0-\mathcal {K}_Y$. By Lemma 8.4, there exist
$y\in Y_0-\mathcal {K}_Y$. By Lemma 8.4, there exist ![]() $|r|<1$ and
$|r|<1$ and ![]() $t=\log (\eta _0\cdot \omega (y)/6)$, where
$t=\log (\eta _0\cdot \omega (y)/6)$, where ![]() $0<\eta _0\leq 1$ is as in (6.6), such that
$0<\eta _0\leq 1$ is as in (6.6), such that
We claim that if ![]() $v\in I_Z(y,{D_1})$, then
$v\in I_Z(y,{D_1})$, then ![]() $v(u_{r}a_{t}) \in I_Z(yu_ra_t, c_1\alpha )$. Firstly, note that, plugging
$v(u_{r}a_{t}) \in I_Z(yu_ra_t, c_1\alpha )$. Firstly, note that, plugging ![]() $t=\log (\eta _0\cdot \omega (y)/6)$ and using
$t=\log (\eta _0\cdot \omega (y)/6)$ and using ![]() $0<\eta \le 1$,
$0<\eta \le 1$,
Hence for ![]() $v\in I_Z(y,{D_1})$, as
$v\in I_Z(y,{D_1})$, as ![]() $\omega (y) \|v\|< D_1^{-1}$,
$\omega (y) \|v\|< D_1^{-1}$,
where we used the fact that ![]() $(c_1\alpha )^{-1}{D_1} > \omega (yu_ra_t)$.
$(c_1\alpha )^{-1}{D_1} > \omega (yu_ra_t)$.
Since ![]() $y(\exp v) u_{r}a_{t} = (y u_ra_t)\exp (v(u_{r}a_t)) \in Z$, this implies that
$y(\exp v) u_{r}a_{t} = (y u_ra_t)\exp (v(u_{r}a_t)) \in Z$, this implies that ![]() $v(u_{r}a_{t}) \in I_Z(yu_ra_t, c_1\alpha )$. Therefore the map
$v(u_{r}a_{t}) \in I_Z(yu_ra_t, c_1\alpha )$. Therefore the map ![]() $v\mapsto v(u_{r}a_{t})$ is an injective map from
$v\mapsto v(u_{r}a_{t})$ is an injective map from ![]() $I_Z(y,{D_1})$ into
$I_Z(y,{D_1})$ into ![]() $I_Z(yu_ra_t, c_1\alpha )$. Consequently,
$I_Z(yu_ra_t, c_1\alpha )$. Consequently,
This finishes the proof.
9. Margulis function: construction and estimate
Throughout this section, we fix closed non-elementary ![]() $H$-orbits
$H$-orbits ![]() $Y, Z$ in
$Y, Z$ in ![]() $X$ and
$X$ and
In this section, we define a family of Margulis functions ![]() $F_{s, \lambda }=F_{s,\lambda, Y, Z}$,
$F_{s, \lambda }=F_{s,\lambda, Y, Z}$, ![]() $\lambda >1$ and show that the hypothesis of Proposition 7.5 is satisfied for a certain choice of
$\lambda >1$ and show that the hypothesis of Proposition 7.5 is satisfied for a certain choice of ![]() $\lambda$, which we will denote by
$\lambda$, which we will denote by ![]() $\lambda _s$. As a consequence, we will get an estimate on
$\lambda _s$. As a consequence, we will get an estimate on ![]() $m_Y(F_{s, \lambda _s})$ in Theorem 9.18.
$m_Y(F_{s, \lambda _s})$ in Theorem 9.18.
We set
for ![]() $D_1>1$ as given in Lemma 8.13.
$D_1>1$ as given in Lemma 8.13.
Definition 9.1 (Margulis function)
(1) Define
 $f_s:=f_{s,Y, Z}:Y_0 \to (0,\infty )$ by
$f_s:=f_{s,Y, Z}:Y_0 \to (0,\infty )$ by
 \[ f_s(y):=\begin{cases}\sum_{v\in I_Z(y)}\|v\|^{-s} & \text{if $I_Z(y)\ne \emptyset$,}\\ \omega(y)^{s} & \text{otherwise}.\end{cases} \]
\[ f_s(y):=\begin{cases}\sum_{v\in I_Z(y)}\|v\|^{-s} & \text{if $I_Z(y)\ne \emptyset$,}\\ \omega(y)^{s} & \text{otherwise}.\end{cases} \]
(2) For
 $\lambda \ge 1$, define
$\lambda \ge 1$, define  $F_{s,\lambda }=F_{s, \lambda, Y, Z}:Y_0\to (0,\infty )$ as follows:
(9.2)
$F_{s,\lambda }=F_{s, \lambda, Y, Z}:Y_0\to (0,\infty )$ as follows:
(9.2) \begin{equation} F_{s, \lambda}(y)=f_{s}(y)+\lambda \;\omega (y)^s. \end{equation}
\begin{equation} F_{s, \lambda}(y)=f_{s}(y)+\lambda \;\omega (y)^s. \end{equation}
Note that for all ![]() $y\in Y_0$
$y\in Y_0$
Since ![]() $Y$ and
$Y$ and ![]() $Z$ are closed orbits, both
$Z$ are closed orbits, both ![]() $f_s$ and
$f_s$ and ![]() $F_{s,\lambda }$ are locally bounded. Moreover, they are also Borel functions. Indeed,
$F_{s,\lambda }$ are locally bounded. Moreover, they are also Borel functions. Indeed, ![]() $\omega ^s$ is continuous on
$\omega ^s$ is continuous on ![]() $Y_0$, and
$Y_0$, and ![]() $f_s$ is continuous on the open subset
$f_s$ is continuous on the open subset ![]() $\{y\in Y_0: I_Z(y)\neq \emptyset \}$ as well as on its complement.
$\{y\in Y_0: I_Z(y)\neq \emptyset \}$ as well as on its complement.
In this section, we specify choices of parameters ![]() $t_s$ and
$t_s$ and ![]() $\lambda _s$ so that the average
$\lambda _s$ so that the average ![]() ${\mathsf {A}}_{t_s}F_{s, \lambda _s}$ satisfies the hypothesis of Proposition 7.5 with controlled size of the additive term (Lemma 9.14).
${\mathsf {A}}_{t_s}F_{s, \lambda _s}$ satisfies the hypothesis of Proposition 7.5 with controlled size of the additive term (Lemma 9.14).
Notation 9.4 (Parameters)
(1) For
 $0< c <1$, define
$0< c <1$, define  $t(c, s)>0$ by
where
$t(c, s)>0$ by
where \[ \frac{ b_0 b_1 {\mathsf{p}}_Y^{\delta_Y} e^{-(\delta_Y -s)t(c,s) /4} }{(\delta_Y-s)}= c \]
\[ \frac{ b_0 b_1 {\mathsf{p}}_Y^{\delta_Y} e^{-(\delta_Y -s)t(c,s) /4} }{(\delta_Y-s)}= c \]
 $b_0$ and
$b_0$ and  $b_1$ are given in Lemma 5.13.
$b_1$ are given in Lemma 5.13.(2) For
 $0< c<1$ and
$0< c<1$ and  $t>0$, define
$t>0$, define  $\lambda (t,c,s)>0$ by
where
$\lambda (t,c,s)>0$ by
where \[ \lambda(t,c,s):=\big( 2 c_0 D_1 p_Y^{6}\tau_Z\big) \frac{ e^{2ts}}{c} \]
\[ \lambda(t,c,s):=\big( 2 c_0 D_1 p_Y^{6}\tau_Z\big) \frac{ e^{2ts}}{c} \]
 $c_0$ is given by (8.13).
$c_0$ is given by (8.13).
As it is evident from the above, the definition of ![]() $t(c,s)$ is motivated by the linear algebra Lemma 5.13. Indeed, for any vector
$t(c,s)$ is motivated by the linear algebra Lemma 5.13. Indeed, for any vector ![]() $v\in e_1G$ and
$v\in e_1G$ and ![]() $t\ge t(c,s)$, we have
$t\ge t(c,s)$, we have
The choice of ![]() $\lambda (t,c,s)$ is to control the additive difference between
$\lambda (t,c,s)$ is to control the additive difference between ![]() $f_s(yu_ra_t )$ and
$f_s(yu_ra_t )$ and ![]() $\sum _{v\in I_Z(y) }\|vu_ra_t\|^{-s}$ uniformly over all
$\sum _{v\in I_Z(y) }\|vu_ra_t\|^{-s}$ uniformly over all ![]() $r\in [-1,1]$ such that
$r\in [-1,1]$ such that ![]() $yu_r\in Y_0$, so that we will get
$yu_r\in Y_0$, so that we will get
(see Lemma 9.11, (9.15) and (9.16)).
Markov operator for the height function
In this subsection, we use notation from § 6.
It will be convenient to introduce the following notation.
Notation 9.6 Let ![]() $Q\subset G$ be a compact subset.
$Q\subset G$ be a compact subset.
(1) Let
 $d_Q\geq 1$ be the infimum of all
$d_Q\geq 1$ be the infimum of all  $d\geq 1$ such that for all
$d\geq 1$ such that for all  $g\in Q$ and
$g\in Q$ and  $v\in \mathbb {R}^4$,
(9.7)Note that
$v\in \mathbb {R}^4$,
(9.7)Note that \begin{equation} d^{-1} \|v\| \le \| vg \|\le d \|v\|. \end{equation}
\begin{equation} d^{-1} \|v\| \le \| vg \|\le d \|v\|. \end{equation} $d_Q\asymp \max _{g\in Q} \|g\|$, up to an absolute multiplicative constant.
$d_Q\asymp \max _{g\in Q} \|g\|$, up to an absolute multiplicative constant.(2) We also define
 $c_Q\geq 1$ to be the infimum of all
$c_Q\geq 1$ to be the infimum of all  $c\geq 1$ such that for any
$c\geq 1$ such that for any  $x\in X_0$,
$x\in X_0$,  $g\in Q$ with
$g\in Q$ with  $xg\in X_0$, and for all
$xg\in X_0$, and for all  $1\le i \le \ell$
(9.8)We note that
$1\le i \le \ell$
(9.8)We note that \begin{equation} c^{-1} \omega_i(x) \le \omega_i(xg)\le c\, \omega_i(x). \end{equation}
\begin{equation} c^{-1} \omega_i(x) \le \omega_i(xg)\le c\, \omega_i(x). \end{equation} $c_Q\asymp \max _{g\in Q} \|g\|$ up to an absolute multiplicative constant.
$c_Q\asymp \max _{g\in Q} \|g\|$ up to an absolute multiplicative constant.
Lemma 9.9 For any ![]() $0< c\leq 1/2$ and
$0< c\leq 1/2$ and ![]() $t \ge t(c, s)$, there exists
$t \ge t(c, s)$, there exists ![]() $D_2\asymp e^{2t}$ so that for all
$D_2\asymp e^{2t}$ so that for all ![]() $y\in Y_0$ and
$y\in Y_0$ and ![]() $1\leq \rho \leq 2$,
$1\leq \rho \leq 2$,
Proof. Let ![]() $t\geq t(c, s)$. We compare
$t\geq t(c, s)$. We compare ![]() $\omega (yu_ra_t)$ and
$\omega (yu_ra_t)$ and ![]() $\omega (y)$ for
$\omega (y)$ for ![]() $r\in [-2,2]$. Setting
$r\in [-2,2]$. Setting
we have ![]() $c_Q \asymp e^t$.
$c_Q \asymp e^t$.
Let ![]() $\eta _0$ be as in Lemma 6.5. Fix
$\eta _0$ be as in Lemma 6.5. Fix ![]() $0<\eta _X\leq \min \{{\varepsilon }_X,\eta _0\}$ so that
$0<\eta _X\leq \min \{{\varepsilon }_X,\eta _0\}$ so that
We consider two cases.
Case 1: ![]() $\omega (y)\leq 2c_Q/\eta _X$. In this case, for
$\omega (y)\leq 2c_Q/\eta _X$. In this case, for ![]() $h\in Q$ with
$h\in Q$ with ![]() $yh\in Y_0$,
$yh\in Y_0$,
Hence, the claim in this case follows if we choose ![]() $D_2=2c_Q^2/\eta _X\asymp e^{2t}$.
$D_2=2c_Q^2/\eta _X\asymp e^{2t}$.
Case 2: ![]() $\omega (y) >2c_Q/\eta _X$. By the definition of
$\omega (y) >2c_Q/\eta _X$. By the definition of ![]() $\omega$, there exists
$\omega$, there exists ![]() $1\le i\le \ell$ such that
$1\le i\le \ell$ such that
By the definition of ![]() $c_Q$, see (9.8), we have
$c_Q$, see (9.8), we have
for all ![]() $h\in Q$ with
$h\in Q$ with ![]() $yh\in Y_0$. Choose
$yh\in Y_0$. Choose ![]() $g_0\in G$ so that
$g_0\in G$ so that ![]() $y=[g_0]$. In view of Lemma 6.5, see in particular (6.6), and since
$y=[g_0]$. In view of Lemma 6.5, see in particular (6.6), and since ![]() $\eta _X\leq \eta _0$ there exists
$\eta _X\leq \eta _0$ there exists ![]() $\gamma \in \Gamma$ such that simultaneously for all
$\gamma \in \Gamma$ such that simultaneously for all ![]() $h\in Q$ with
$h\in Q$ with ![]() $yh\in Y_0$,
$yh\in Y_0$,
Since ![]() $v_i=e_1g_i^{-1} \in e_1G$ (see (6.1)), we may apply Lemma 5.13 (linear algebra lemma II) and deduce
$v_i=e_1g_i^{-1} \in e_1G$ (see (6.1)), we may apply Lemma 5.13 (linear algebra lemma II) and deduce
 \begin{align*} {\mathsf{A}}_{t,\rho}\omega(y)^s&=\frac{1}{\mu_y([-\rho,\rho])}\int_{-\rho}^{\rho} \frac{1}{\| v_{i}\gamma u_r a_t \|^s} \,d\mu_y(r)\\ &\leq \frac{ b_0b_1{\mathsf{p}}_Y^{\delta_Y} e^{-(\delta_Y-s) t/4 } }{(\delta_Y-s)} \|v_{i}\gamma\|^{-s}\le c\cdot \omega(y)^s; \end{align*}
\begin{align*} {\mathsf{A}}_{t,\rho}\omega(y)^s&=\frac{1}{\mu_y([-\rho,\rho])}\int_{-\rho}^{\rho} \frac{1}{\| v_{i}\gamma u_r a_t \|^s} \,d\mu_y(r)\\ &\leq \frac{ b_0b_1{\mathsf{p}}_Y^{\delta_Y} e^{-(\delta_Y-s) t/4 } }{(\delta_Y-s)} \|v_{i}\gamma\|^{-s}\le c\cdot \omega(y)^s; \end{align*}
in the last inequality we used the fact that ![]() $t\geq t(c,s)$. The proof is now complete.
$t\geq t(c,s)$. The proof is now complete.
Log-continuity of  $F_{s,\lambda }$
$F_{s,\lambda }$
The following log-continuity lemma with a control on the multiplicative constant ![]() $\sigma$ is the first hypothesis in Proposition 7.5.
$\sigma$ is the first hypothesis in Proposition 7.5.
Lemma 9.10 (Log-continuity lemma)
There exists ![]() $2\le \sigma \ll {\mathsf {p}}_Y^{8}$ so that the following holds: for every
$2\le \sigma \ll {\mathsf {p}}_Y^{8}$ so that the following holds: for every ![]() $\lambda \geq \tau _Z$, we have
$\lambda \geq \tau _Z$, we have
for all ![]() $y\in Y_0$ and all
$y\in Y_0$ and all ![]() $h\in B_H(2)$ so that
$h\in B_H(2)$ so that ![]() $yh\in Y_0$.
$yh\in Y_0$.
Let ![]() $c_0$ be as in Lemma 8.13. Recall from Theorem 3.3 that
$c_0$ be as in Lemma 8.13. Recall from Theorem 3.3 that ![]() $\tau _Z\geq {\varepsilon }_X^2$, replacing
$\tau _Z\geq {\varepsilon }_X^2$, replacing ![]() $c_0$ by its multiple (which we continue to denote by
$c_0$ by its multiple (which we continue to denote by ![]() $c_0$) if necessary we assume that
$c_0$) if necessary we assume that ![]() $c_0\tau _Z\geq 1$.
$c_0\tau _Z\geq 1$.
We first obtain the following estimate for ![]() $f$ on nearby points.
$f$ on nearby points.
Lemma 9.11 Let ![]() $Q\subset H$ be a compact subset. For any
$Q\subset H$ be a compact subset. For any ![]() $y\in Y_0$ and
$y\in Y_0$ and ![]() $h\in Q$ such that
$h\in Q$ such that ![]() $yh\in Y_0$, we have
$yh\in Y_0$, we have
where ![]() $c_0$ is as above and the sum is understood as
$c_0$ is as above and the sum is understood as ![]() $0$ when
$0$ when ![]() $I_Z(y)=\emptyset$.
$I_Z(y)=\emptyset$.
Proof. Let ![]() $y\in Y_0$ and
$y\in Y_0$ and ![]() $h\in Q$ with
$h\in Q$ with ![]() $yh\in Y_0$. If
$yh\in Y_0$. If ![]() $I_Z(yh)=\emptyset$, then by (9.8), we have
$I_Z(yh)=\emptyset$, then by (9.8), we have
proving the claim; recall that ![]() $c_0\tau _Z\geq 1$.
$c_0\tau _Z\geq 1$.
Now suppose that ![]() $I_Z(yh)\ne \emptyset$. Setting
$I_Z(yh)\ne \emptyset$. Setting
we write
Since ![]() $\# I_Z(yh)\le c_0 {\mathsf {p}}_Y^{6} \tau _Z$ by Lemma 8.13, we have
$\# I_Z(yh)\le c_0 {\mathsf {p}}_Y^{6} \tau _Z$ by Lemma 8.13, we have
Thus, if there is no ![]() $v\in I_Z(yh)$ with
$v\in I_Z(yh)$ with ![]() $\|v\|\le {\varepsilon }$, then the lemma follows from (9.12).
$\|v\|\le {\varepsilon }$, then the lemma follows from (9.12).
If ![]() $v\in I_Z(yh)$ satisfies
$v\in I_Z(yh)$ satisfies ![]() $\|v\|< \varepsilon$, then
$\|v\|< \varepsilon$, then
in particular, ![]() $vh^{-1}\in I_Z(y)$. Therefore, by setting
$vh^{-1}\in I_Z(y)$. Therefore, by setting ![]() $v'=vh^{-1}$,
$v'=vh^{-1}$,
Together with (9.13), this finishes the proof.
Proof of Lemma 9.10 Since ![]() $B_H(2)^{-1}=B_H(2)$, it suffices to show the inequality
$B_H(2)^{-1}=B_H(2)$, it suffices to show the inequality ![]() $\le$. By Lemma 9.11, applied with
$\le$. By Lemma 9.11, applied with ![]() $Q=B_H(2)$,
$Q=B_H(2)$, ![]() $c:=c_{B_H(2)}$ and
$c:=c_{B_H(2)}$ and ![]() $d:=d_{B_H(2)}$, we have that for all
$d:=d_{B_H(2)}$, we have that for all ![]() $h\in B_H(1)$ with
$h\in B_H(1)$ with ![]() $yh\in Y_0$, we have
$yh\in Y_0$, we have
 \begin{align*} f_{s}(yh)&\le \sum_{v\in I_Z(y)} \|vh \|^{-s} +{}\big( {c_0} c d D_1 {\mathsf{p}}_Y^{6} \tau_Z \big) \omega(y)^s \\ &\leq d \sum_{v\in I_Z(y)} \|v\|^{-s} +{}c_0c d D_1 {\mathsf{p}}_Y^{6}\tau_Z \omega(y)^s, \end{align*}
\begin{align*} f_{s}(yh)&\le \sum_{v\in I_Z(y)} \|vh \|^{-s} +{}\big( {c_0} c d D_1 {\mathsf{p}}_Y^{6} \tau_Z \big) \omega(y)^s \\ &\leq d \sum_{v\in I_Z(y)} \|v\|^{-s} +{}c_0c d D_1 {\mathsf{p}}_Y^{6}\tau_Z \omega(y)^s, \end{align*}
where we have used the definition of ![]() $d$.
$d$.
Recall from Theorem 3.3 that ![]() ${\varepsilon }_X^2\leq \tau _Z\leq \lambda$ and that
${\varepsilon }_X^2\leq \tau _Z\leq \lambda$ and that ![]() $D_1\ll \mathsf {p}_Y^2$.
$D_1\ll \mathsf {p}_Y^2$.
If ![]() $I_Z(y)=\emptyset$, then
$I_Z(y)=\emptyset$, then
 \begin{align*} F_{s,\lambda}(yh)&\ll {\mathsf{p}}_Y^8 \tau_Z\omega (y)^s+\lambda \omega(y)^s\ll \mathsf{p}_Y^{8} \lambda \omega(y)^s\\ &\ll {\mathsf{p}}_Y^{8} (f_{s}(y) + \lambda \omega(y)^s)\ll{\mathsf{p}}_Y^{8} F_{s,\lambda}(y). \end{align*}
\begin{align*} F_{s,\lambda}(yh)&\ll {\mathsf{p}}_Y^8 \tau_Z\omega (y)^s+\lambda \omega(y)^s\ll \mathsf{p}_Y^{8} \lambda \omega(y)^s\\ &\ll {\mathsf{p}}_Y^{8} (f_{s}(y) + \lambda \omega(y)^s)\ll{\mathsf{p}}_Y^{8} F_{s,\lambda}(y). \end{align*}
If ![]() $I_Z(y)\ne \emptyset$, then
$I_Z(y)\ne \emptyset$, then
 \begin{align*} F_{s,\lambda}(yh)&\leq d\cdot f_{s}(y)+ {}c_0c d D_1 {\mathsf{p}}_Y^{6}\tau_Z \omega(y)^s +\lambda\omega(yh)^s\\ &\ll f_{s}(y)+\mathsf{p}_Y^{8} \lambda\omega(y)^s \ll \mathsf{p}_Y^{8} F_{s,\lambda}(y). \end{align*}
\begin{align*} F_{s,\lambda}(yh)&\leq d\cdot f_{s}(y)+ {}c_0c d D_1 {\mathsf{p}}_Y^{6}\tau_Z \omega(y)^s +\lambda\omega(yh)^s\\ &\ll f_{s}(y)+\mathsf{p}_Y^{8} \lambda\omega(y)^s \ll \mathsf{p}_Y^{8} F_{s,\lambda}(y). \end{align*}
This finishes the upper bound. The lower bound can be obtained similarly.
Main inequality
We will apply the following lemma to obtain the second hypothesis of Proposition 7.5 for ![]() $c:=(8\sigma \mathsf {p}_Y^{\delta _Y})^{-1}<1/2$.
$c:=(8\sigma \mathsf {p}_Y^{\delta _Y})^{-1}<1/2$.
Lemma 9.14 (Main inequality)
Let ![]() $0< c\leq 1/2$. For
$0< c\leq 1/2$. For ![]() $t\geq t(c/2,s)$ and
$t\geq t(c/2,s)$ and ![]() $\lambda =\lambda (t,c,s)$, we have the following: for any
$\lambda =\lambda (t,c,s)$, we have the following: for any ![]() $y\in Y_0$ and
$y\in Y_0$ and ![]() $1\leq \rho \leq 2$, we have
$1\leq \rho \leq 2$, we have
where ![]() ${D_2} \ll e^{2t}$ is as in Lemma 9.9.
${D_2} \ll e^{2t}$ is as in Lemma 9.9.
Proof. The following argument is based on comparing the values of ![]() $f_{s}(yu_ra_t)$ and
$f_{s}(yu_ra_t)$ and ![]() $f_{s}(y)$ for
$f_{s}(y)$ for ![]() $r\in [-2,2]$ such that
$r\in [-2,2]$ such that ![]() $yu_ra_t\in Y_0$.
$yu_ra_t\in Y_0$.
Let ![]() $Q:=\{a_\tau u_r: |r| \le 2 , |\tau |\leq t\}$. Then
$Q:=\{a_\tau u_r: |r| \le 2 , |\tau |\leq t\}$. Then
where ![]() $c_Q$ and
$c_Q$ and ![]() $d_Q$ are as in (9.6). Hence, by Lemma 9.11, we have that for any
$d_Q$ are as in (9.6). Hence, by Lemma 9.11, we have that for any ![]() $|r|\le 2$ such that
$|r|\le 2$ such that ![]() $yu_ra_t\in Y_0$,
$yu_ra_t\in Y_0$,
where ![]() $c_0$ is as in Lemma 9.11.
$c_0$ is as in Lemma 9.11.
By averaging (9.15) over ![]() $[-\rho,\rho ]$ with respect to
$[-\rho,\rho ]$ with respect to ![]() $\mu _y$, and applying (9.5), we get
$\mu _y$, and applying (9.5), we get
 \begin{align} {\mathsf{A}}_{t,\rho} f_{s}(y)&\leq c\cdot f_{s}(y)+ c_0 D_1 {\mathsf{p}}_Y^{6} \tau_Z \omega(y)^{s} e^{2ts} \nonumber\\ &\leq c\cdot f_{s}(y)+ \frac{\lambda c}{2} \omega(y)^{s}. \end{align}
\begin{align} {\mathsf{A}}_{t,\rho} f_{s}(y)&\leq c\cdot f_{s}(y)+ c_0 D_1 {\mathsf{p}}_Y^{6} \tau_Z \omega(y)^{s} e^{2ts} \nonumber\\ &\leq c\cdot f_{s}(y)+ \frac{\lambda c}{2} \omega(y)^{s}. \end{align}Then by Lemma 9.9 and (9.16), we have
 \begin{align*} {\mathsf{A}}_{t,\rho} F_{s,\lambda}(y) & = {\mathsf{A}}_{t,\rho} f_{s}(y)+ {\mathsf{A}}_{t,\rho} \lambda\omega(y)^s \\ &\leq c\cdot f_{s}(y)+\frac{c\lambda}{2}\omega(y)^{s}+\frac{c\lambda}{2}\omega(y)^{s}+\lambda D_2\\ &=c\cdot F_{s,\lambda}(y)+\lambda D_2. \end{align*}
\begin{align*} {\mathsf{A}}_{t,\rho} F_{s,\lambda}(y) & = {\mathsf{A}}_{t,\rho} f_{s}(y)+ {\mathsf{A}}_{t,\rho} \lambda\omega(y)^s \\ &\leq c\cdot f_{s}(y)+\frac{c\lambda}{2}\omega(y)^{s}+\frac{c\lambda}{2}\omega(y)^{s}+\lambda D_2\\ &=c\cdot F_{s,\lambda}(y)+\lambda D_2. \end{align*}
By Theorem 4.8, we have ![]() $\mathsf {s}_Y\asymp {\mathsf {p}}_Y$. For the sake of simplicity of notation, we put
$\mathsf {s}_Y\asymp {\mathsf {p}}_Y$. For the sake of simplicity of notation, we put
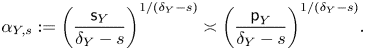 \begin{equation} \alpha_{Y,s}:=\bigg(\frac{{\mathsf{s}}_Y}{ \delta_Y-s}\bigg) ^{1/ (\delta_Y-s)} \asymp \bigg(\frac{{\mathsf{p}}_Y}{ \delta_Y-s}\bigg) ^{1/ (\delta_Y-s)}.\end{equation}
\begin{equation} \alpha_{Y,s}:=\bigg(\frac{{\mathsf{s}}_Y}{ \delta_Y-s}\bigg) ^{1/ (\delta_Y-s)} \asymp \bigg(\frac{{\mathsf{p}}_Y}{ \delta_Y-s}\bigg) ^{1/ (\delta_Y-s)}.\end{equation}We are now in a position to apply Proposition 7.5 to get the following estimate.
Theorem 9.18 (Margulis function on average)
There exists ![]() $\lambda _s>1$ such that
$\lambda _s>1$ such that
Proof. Let ![]() $1\leq \sigma \ll \mathsf {p}_Y^8$ be given by Lemma 9.10. Let
$1\leq \sigma \ll \mathsf {p}_Y^8$ be given by Lemma 9.10. Let ![]() $c:=(8\sigma \mathsf {p}_Y^{\delta _Y})^{-1}<1/2$,
$c:=(8\sigma \mathsf {p}_Y^{\delta _Y})^{-1}<1/2$, ![]() $t_s:= t(c, s)$ and
$t_s:= t(c, s)$ and ![]() $\lambda _s:=\lambda ( t_s,c, s)$ be given by (9.4). Then in view of Lemmas 9.10 and 9.14,
$\lambda _s:=\lambda ( t_s,c, s)$ be given by (9.4). Then in view of Lemmas 9.10 and 9.14, ![]() $F_{s,\lambda _s}$ satisfies the conditions of Proposition 7.5 with
$F_{s,\lambda _s}$ satisfies the conditions of Proposition 7.5 with ![]() $t=t_s$ and
$t=t_s$ and ![]() $D_0=\lambda _s D_2$, where
$D_0=\lambda _s D_2$, where ![]() $D_2\ll e^{2t_s}$ is given in Lemma 9.9. Therefore
$D_2\ll e^{2t_s}$ is given in Lemma 9.9. Therefore
Since
we get
Combining this with (9.19) finishes the proof.
10. Quantitative isolation of a closed orbit
In this section, we deduce Theorem 1.5 from Theorem 9.18. Let ![]() $Y, Z$ be non-elementary closed
$Y, Z$ be non-elementary closed ![]() $H$-orbits in
$H$-orbits in ![]() $X$. We allow the case
$X$. We allow the case ![]() $Y=Z$ as well. Let
$Y=Z$ as well. Let ![]() $ {\delta _Y}/{3} \le s< \delta _Y$.
$ {\delta _Y}/{3} \le s< \delta _Y$.
Recall the definitions of ![]() $f_s=f_{s,Y, Z}$ and
$f_s=f_{s,Y, Z}$ and ![]() $F_{s,\lambda }=F_{s,\lambda, Y, Z}$ from Definition 9.1. Let
$F_{s,\lambda }=F_{s,\lambda, Y, Z}$ from Definition 9.1. Let ![]() $\lambda _s$ be given by Theorem 9.18. Using the log-continuity lemma for
$\lambda _s$ be given by Theorem 9.18. Using the log-continuity lemma for ![]() $F_{s,\lambda _s}$ (Lemma 9.10), we first deduce the following estimate.
$F_{s,\lambda _s}$ (Lemma 9.10), we first deduce the following estimate.
Proposition 10.1 For any ![]() $0<\varepsilon <{\varepsilon }_X$ and
$0<\varepsilon <{\varepsilon }_X$ and ![]() $y\in Y_0\cap X_\varepsilon$, we have
$y\in Y_0\cap X_\varepsilon$, we have
Proof. Let ![]() $y\in Y_0\cap X_{\varepsilon }$. Then
$y\in Y_0\cap X_{\varepsilon }$. Then ![]() $\operatorname {inj}(y)\ge {\varepsilon }$ and hence
$\operatorname {inj}(y)\ge {\varepsilon }$ and hence ![]() $y B_H({\varepsilon })= B(y, {\varepsilon })$. For all
$y B_H({\varepsilon })= B(y, {\varepsilon })$. For all ![]() $h\in B_H({\varepsilon }_X)$,
$h\in B_H({\varepsilon }_X)$, ![]() $F_{s,\lambda _s} (y) \le \sigma F_{s,\lambda _s}(yh)$ for some constant
$F_{s,\lambda _s} (y) \le \sigma F_{s,\lambda _s}(yh)$ for some constant ![]() $\sigma \ll \mathsf {p}_Y^{6}$ by Lemma 9.10. By applying Theorem 9.18, we get
$\sigma \ll \mathsf {p}_Y^{6}$ by Lemma 9.10. By applying Theorem 9.18, we get
 \[ F_{s, \lambda_s} (y) \le \frac{ \sigma \int_{x\in y B_H({\varepsilon})} F_{s,\lambda_s}(x) \,dm_Y(x)}{m_Y(B(y, {\varepsilon}))}\le \frac{ \sigma \cdot m_Y(F_{s,\lambda_s})}{m_Y(B(y, {\varepsilon}))} \ll \frac{\alpha_{Y, s}^\star \tau_Z }{m_Y(B(y, {\varepsilon}))}. \]
\[ F_{s, \lambda_s} (y) \le \frac{ \sigma \int_{x\in y B_H({\varepsilon})} F_{s,\lambda_s}(x) \,dm_Y(x)}{m_Y(B(y, {\varepsilon}))}\le \frac{ \sigma \cdot m_Y(F_{s,\lambda_s})}{m_Y(B(y, {\varepsilon}))} \ll \frac{\alpha_{Y, s}^\star \tau_Z }{m_Y(B(y, {\varepsilon}))}. \]
Recall from (6.8) that for all ![]() $x\in X_0$,
$x\in X_0$,
Using the next lemma, we will be able to use the estimate for ![]() $f_{s, Y, Z}$ obtained in Proposition 10.1 to deduce a lower bound for
$f_{s, Y, Z}$ obtained in Proposition 10.1 to deduce a lower bound for ![]() $d(y, Z)$.
$d(y, Z)$.
Lemma 10.3
(1) Let
 $y\in Y_0$ and
$y\in Y_0$ and  $z\in Z- B_Y(y, \operatorname {inj}(y))$. If
$z\in Z- B_Y(y, \operatorname {inj}(y))$. If  $d(y, z) \le ({1}/{2\alpha c_1D_1})\operatorname {inj}(y)$, then
where
$d(y, z) \le ({1}/{2\alpha c_1D_1})\operatorname {inj}(y)$, then
where \[ d(y, z)^{-s}\le c_1 f_{s, Y, Z}(y) \]
\[ d(y, z)^{-s}\le c_1 f_{s, Y, Z}(y) \]
 $c_1\ge 1$ is as in (8.1).
$c_1\ge 1$ is as in (8.1).(2) If
 $Y\ne Z$, then for any
$Y\ne Z$, then for any  $y\in Y_0$,
$y\in Y_0$,
 \[ d(y, Z)^{-s} \ll \mathsf{p}_Y^2 f_{s,Y, Z}(y). \]
\[ d(y, Z)^{-s} \ll \mathsf{p}_Y^2 f_{s,Y, Z}(y). \]
Proof. As ![]() $Z$ is closed and
$Z$ is closed and ![]() $d(y, z) \le ({1}/{2\alpha c_1D_1})\operatorname {inj} (y) <\frac {1}{2} \operatorname {inj}(y)$, the hypothesis
$d(y, z) \le ({1}/{2\alpha c_1D_1})\operatorname {inj} (y) <\frac {1}{2} \operatorname {inj}(y)$, the hypothesis ![]() $z\in Z- B_Y(y, \operatorname {inj}(y))$ and the choice of
$z\in Z- B_Y(y, \operatorname {inj}(y))$ and the choice of ![]() $c_1$ implies that
$c_1$ implies that ![]() $z$ is of the form
$z$ is of the form ![]() $y\exp (v)\exp (v')$ with
$y\exp (v)\exp (v')$ with ![]() $v\in i \mathfrak {sl}_2(\mathbb {R})-\{0\}$ and
$v\in i \mathfrak {sl}_2(\mathbb {R})-\{0\}$ and ![]() $v'\in \mathfrak {sl}_2(\mathbb {R})$.
$v'\in \mathfrak {sl}_2(\mathbb {R})$.
In particular ![]() $y\exp (v)=z\exp (-v')\in Z$. Moreover, by (8.1),
$y\exp (v)=z\exp (-v')\in Z$. Moreover, by (8.1),
It follows that ![]() $v\in I_Z(y, D_1)$. Therefore
$v\in I_Z(y, D_1)$. Therefore
proving (1).
We now turn to the proof of (2); suppose thus that ![]() $Y\ne Z$. Then there exists
$Y\ne Z$. Then there exists ![]() $z\in Z$ such that
$z\in Z$ such that ![]() $d(y, Z)=d(y,z)$. In view of (1), it suffices to consider the case when
$d(y, Z)=d(y,z)$. In view of (1), it suffices to consider the case when ![]() $d(y, z)> ({1}/{2\alpha c_1D_1})\operatorname {inj}(y)$.
$d(y, z)> ({1}/{2\alpha c_1D_1})\operatorname {inj}(y)$.
Since ![]() $s\leq 1$,
$s\leq 1$, ![]() $\omega (y)^s\le f_s(y)$, and
$\omega (y)^s\le f_s(y)$, and ![]() $D_1\ll \mathsf {p}_Y^2$, we get
$D_1\ll \mathsf {p}_Y^2$, we get
where we also used (10.2). The proof is complete.
Theorem 1.5(1) is a special case of the following theorem.
Theorem 10.5 (Isolation in distance)
For any ![]() $0<\varepsilon <{\varepsilon }_X$,
$0<\varepsilon <{\varepsilon }_X$, ![]() $y\in Y_0\cap X_\varepsilon$, and
$y\in Y_0\cap X_\varepsilon$, and ![]() $z\in Z$, at least one of the following holds:
$z\in Z$, at least one of the following holds:
(1)
 $z\in B_Y(y,{\varepsilon })=yB_H(e,{\varepsilon })$; or
$z\in B_Y(y,{\varepsilon })=yB_H(e,{\varepsilon })$; or(2)
 $d(y,z)\gg \alpha _{Y,s}^{-\star /s} {m_Y(B(y, {\varepsilon }))}^{1/s} {\tau _Z}^{-1/s}$, where
$d(y,z)\gg \alpha _{Y,s}^{-\star /s} {m_Y(B(y, {\varepsilon }))}^{1/s} {\tau _Z}^{-1/s}$, where  $\alpha _{Y,s}$ is as given in (9.17).
$\alpha _{Y,s}$ is as given in (9.17).
Proof. As ![]() $y\in X_{\varepsilon }$,
$y\in X_{\varepsilon }$, ![]() $\operatorname {inj}(y)\ge {\varepsilon }$. Suppose that
$\operatorname {inj}(y)\ge {\varepsilon }$. Suppose that ![]() $z\notin B_Y(y, {\varepsilon })$. We first observe that since
$z\notin B_Y(y, {\varepsilon })$. We first observe that since ![]() $m_Y(B(y, {\varepsilon }))^{1/s}\ll {\varepsilon }$ and
$m_Y(B(y, {\varepsilon }))^{1/s}\ll {\varepsilon }$ and ![]() $\mathsf {p}_Y^{-2}\gg \alpha _{Y,s}^{-\star /s}$, we have
$\mathsf {p}_Y^{-2}\gg \alpha _{Y,s}^{-\star /s}$, we have
Therefore, if ![]() $d(y, z) \ge ({1}/{2\alpha c_1D_1}){\varepsilon }$, then
$d(y, z) \ge ({1}/{2\alpha c_1D_1}){\varepsilon }$, then ![]() $(2)$ holds in view of the fact that
$(2)$ holds in view of the fact that ![]() $\tau _Z\ge {\varepsilon }_X^2$.
$\tau _Z\ge {\varepsilon }_X^2$.
If ![]() $d(y, z) \le ({1}/{2\alpha c_1D_1}){\varepsilon }\le ({1}/{2\alpha c_1D_1})\operatorname {inj} (y)$, then by Lemma 10.3,
$d(y, z) \le ({1}/{2\alpha c_1D_1}){\varepsilon }\le ({1}/{2\alpha c_1D_1})\operatorname {inj} (y)$, then by Lemma 10.3, ![]() $d(y, z)^{-s} \le c_1 f_{s}(y)$. Hence applying Proposition 10.1, we conclude
$d(y, z)^{-s} \le c_1 f_{s}(y)$. Hence applying Proposition 10.1, we conclude
which finishes the proof in this case as well.
The following theorem is Theorem 1.5(2).
Theorem 10.6 (Isolation in measure)
Let ![]() $0<\varepsilon \leq {\varepsilon }_X$. Let
$0<\varepsilon \leq {\varepsilon }_X$. Let ![]() $Y\ne Z$. We have
$Y\ne Z$. We have
Proof. Let ![]() $\lambda _s$ be given by Theorem 9.18. By Lemma 10.3(2),
$\lambda _s$ be given by Theorem 9.18. By Lemma 10.3(2),
for some ![]() $1< C\ll \mathsf {p}_Y^2$.
$1< C\ll \mathsf {p}_Y^2$.
For ![]() $0<{\varepsilon }<{\varepsilon }_X$, if we set
$0<{\varepsilon }<{\varepsilon }_X$, if we set
then ![]() $\{y\in Y_0: d(y, Z)\le \varepsilon \} \subset \Omega _{\varepsilon }$. On the other hand, we have
$\{y\in Y_0: d(y, Z)\le \varepsilon \} \subset \Omega _{\varepsilon }$. On the other hand, we have
Since ![]() $m_Y(F_{s,\lambda _s}) \ll \alpha _{Y, s}^{\star } \tau _Z$ by Theorem 9.18, we get that
$m_Y(F_{s,\lambda _s}) \ll \alpha _{Y, s}^{\star } \tau _Z$ by Theorem 9.18, we get that
Proof of Proposition 1.17 Let ![]() $F_s=F_{s, \lambda _s}$ be as in Theorem 9.18. Then
$F_s=F_{s, \lambda _s}$ be as in Theorem 9.18. Then ![]() $F_s$ satisfies (1) in the proposition by Lemma 10.3. It satisfies (3) by Lemma 9.10.
$F_s$ satisfies (1) in the proposition by Lemma 10.3. It satisfies (3) by Lemma 9.10.
Moreover, in view of Lemmas 9.10 and 9.14, ![]() $F_{s}$ satisfies the conditions of Proposition 7.5. Hence, by Proposition 7.6, it also satisfies (2) in the proposition.
$F_{s}$ satisfies the conditions of Proposition 7.5. Hence, by Proposition 7.6, it also satisfies (2) in the proposition.
We remark that in both Theorems 10.5 and 10.6, the exponents ![]() $\star$ depend only on
$\star$ depend only on ![]() $G$, and the implied constants are respectively of the form
$G$, and the implied constants are respectively of the form ![]() $c\,{\varepsilon }_X^{N}$ and
$c\,{\varepsilon }_X^{N}$ and ![]() $c^{-1} \,{\varepsilon }_X^{-N}$ for some
$c^{-1} \,{\varepsilon }_X^{-N}$ for some ![]() $c\le 1$ and
$c\le 1$ and ![]() $N\ge 1$ both depending only on
$N\ge 1$ both depending only on ![]() $G$.
$G$.
Number of properly immersed geodesic planes
When ![]() $\operatorname {Vol}(M)<\infty$, we record the following corollary of Theorem 10.5. Let
$\operatorname {Vol}(M)<\infty$, we record the following corollary of Theorem 10.5. Let ![]() $\mathcal {N}(T)$ denote the number of properly immersed totally geodesic planes
$\mathcal {N}(T)$ denote the number of properly immersed totally geodesic planes ![]() $P$ in
$P$ in ![]() $M$ of area at most
$M$ of area at most ![]() $T$.
$T$.
We deduce the following upper bound from Theorem 10.5 using the pigeonhole principle.
Corollary 10.7 Let ![]() $\operatorname {Vol} (M)<\infty$. There exists
$\operatorname {Vol} (M)<\infty$. There exists ![]() $N\ge 1$ (depending only on
$N\ge 1$ (depending only on ![]() $G$) such that for any
$G$) such that for any ![]() $1/2< s<1$, we have
$1/2< s<1$, we have
where the implied constant depends only on ![]() $s$.
$s$.
Proof. We begin by recalling that ![]() $\alpha _{Y,s}=\alpha _s:=( {1}/({1-s}))^{1/(1-s)}$ for any closed
$\alpha _{Y,s}=\alpha _s:=( {1}/({1-s}))^{1/(1-s)}$ for any closed ![]() $H$-orbit
$H$-orbit ![]() $Y$ in
$Y$ in ![]() $X$ when
$X$ when ![]() $\operatorname {Vol} (M)<\infty$.
$\operatorname {Vol} (M)<\infty$.
We obtain an upper bound for the number of closed ![]() $H$-orbits in
$H$-orbits in ![]() $X$ which yields the above result. The proof is based on applying Theorem 10.5.
$X$ which yields the above result. The proof is based on applying Theorem 10.5.
If ![]() $X$ is compact, let
$X$ is compact, let ![]() $\rho =0.1{\varepsilon }_X$. If
$\rho =0.1{\varepsilon }_X$. If ![]() $X$ is not compact, then the quantitative non-divergence of the action of
$X$ is not compact, then the quantitative non-divergence of the action of ![]() $U$ on
$U$ on ![]() $X$ implies that there exists
$X$ implies that there exists ![]() $\rho >0$ so that for all
$\rho >0$ so that for all ![]() $x\in X$ such that
$x\in X$ such that ![]() $xU$ is not compact,
$xU$ is not compact,
for all sufficiently large ![]() $T\gg 1$, e.g. see [Reference Dani and MargulisDM91]. Moreover,
$T\gg 1$, e.g. see [Reference Dani and MargulisDM91]. Moreover, ![]() $\rho$ can be taken to be
$\rho$ can be taken to be ![]() $\asymp {\varepsilon }_X^k$ for some
$\asymp {\varepsilon }_X^k$ for some ![]() $k\ge 1$.
$k\ge 1$.
Since ![]() $(Y, m_Y)$ is
$(Y, m_Y)$ is ![]() $U$-ergodic by the Moore's ergodicity theorem for every closed orbit
$U$-ergodic by the Moore's ergodicity theorem for every closed orbit ![]() $Y=xH$, the Birkhoff ergodic theorem says that for
$Y=xH$, the Birkhoff ergodic theorem says that for ![]() $m_Y$ a.e.
$m_Y$ a.e. ![]() $y\in Y$,
$y\in Y$,
where ![]() $\ell$ denotes the Lebesgue measure on
$\ell$ denotes the Lebesgue measure on ![]() $\mathbb {R}$; therefore
$\mathbb {R}$; therefore
For every ![]() $S>0$ put
$S>0$ put
In view of the above choice of ![]() $\rho$, we have
$\rho$, we have ![]() $\operatorname {Vol}(xH)\geq \rho ^{3}\gg 1$ for every closed orbit
$\operatorname {Vol}(xH)\geq \rho ^{3}\gg 1$ for every closed orbit ![]() $xH$. Let
$xH$. Let ![]() $n_0=\lfloor 3\log _2(\rho )\rfloor$, and for every
$n_0=\lfloor 3\log _2(\rho )\rfloor$, and for every ![]() $T>1$, let
$T>1$, let ![]() $n_T=\lceil \log _2 T\rceil$. Then we have
$n_T=\lceil \log _2 T\rceil$. Then we have
 \[ \{xH: \text{$xH$ is closed and $\operatorname{vol}(xH)\leq T$}\}\subset \bigcup_{n_0}^{n_T} \mathcal{Y}(2^k). \]
\[ \{xH: \text{$xH$ is closed and $\operatorname{vol}(xH)\leq T$}\}\subset \bigcup_{n_0}^{n_T} \mathcal{Y}(2^k). \]
Let ![]() $\eta \asymp \rho$ be so that the map
$\eta \asymp \rho$ be so that the map ![]() $g\mapsto xg$ is injective for all
$g\mapsto xg$ is injective for all ![]() $x\in X_\rho$ and all
$x\in X_\rho$ and all
Fix some ![]() $1/2< s<1$ and some
$1/2< s<1$ and some ![]() $z\in X$. We claim that
$z\in X$. We claim that
where the implied constant depends on ![]() $\rho$.
$\rho$.
For any connected component ![]() $C$ of
$C$ of ![]() $\mathcal {Y}(2^k)\cap z.{\rm Box}(\eta )$, there exists some
$\mathcal {Y}(2^k)\cap z.{\rm Box}(\eta )$, there exists some ![]() $v\in i\mathfrak {sl}_2(\mathbb {R})$ so that
$v\in i\mathfrak {sl}_2(\mathbb {R})$ so that
Let us write ![]() $C=C_v$. Now in view of Theorem 10.5, for every two connected components
$C=C_v$. Now in view of Theorem 10.5, for every two connected components ![]() $C_v\neq C_{v'}$, we have
$C_v\neq C_{v'}$, we have
Because ![]() $\dim (\mathfrak {r})=3$, the cardinality of an
$\dim (\mathfrak {r})=3$, the cardinality of an ![]() $\alpha _s^{-4/s}2^{-2k/s}$-separated set in
$\alpha _s^{-4/s}2^{-2k/s}$-separated set in ![]() $B_{i\mathfrak {sl}_2(\mathbb {R})}(0,\eta )$ is
$B_{i\mathfrak {sl}_2(\mathbb {R})}(0,\eta )$ is ![]() $\ll \alpha _s^{12/s}2^{6k/s}$, where the implied constant depends only on the choice of norm. The claim in (10.9) thus follows from (10.10).
$\ll \alpha _s^{12/s}2^{6k/s}$, where the implied constant depends only on the choice of norm. The claim in (10.9) thus follows from (10.10).
Let ![]() $\bigl \{z_j.{\rm Box}(\eta ): 1\leq j\leq R\bigr \}$ be a covering of
$\bigl \{z_j.{\rm Box}(\eta ): 1\leq j\leq R\bigr \}$ be a covering of ![]() $X_\rho$ with sets of the form
$X_\rho$ with sets of the form ![]() $z.{\rm Box}(\eta )$; we may find such a covering with
$z.{\rm Box}(\eta )$; we may find such a covering with ![]() $R=O(\operatorname {Vol}(X)\eta ^{-6})$ the implied constant is absolute (see also the definition of
$R=O(\operatorname {Vol}(X)\eta ^{-6})$ the implied constant is absolute (see also the definition of ![]() $c_1$ in (8.1)). Then we compute
$c_1$ in (8.1)). Then we compute
 \begin{align*}
\begin{aligned}
\mathcal{N}(2^k)&\leq 2^{-k+1}\sum_{\mathcal{Y}(2^k)} \operatorname{vol}(xH)&\quad&\text{by the
definition of $\mathcal{Y}(2^k)$}\\
&\ll 2^{-k}\sum_{j=1}^{M} \sum_{C_v\subset z_j.{\rm Box}(\eta)} \operatorname{vol}(C_v)&\quad&\text{by (10.8)}\\
&\ll \alpha_s^{12/s}\sum_{j=1}^{R} 2^{{6k}/{s}-k} &\quad& \text{by (10.9)} \\
&\ll {\operatorname{Vol} (X)}\alpha_s^{12/s}2^{{6k}/{s}-k}&\quad&\text{since~$R=O(\operatorname{Vol}(X))$;}
\end{aligned}\end{align*}
\begin{align*}
\begin{aligned}
\mathcal{N}(2^k)&\leq 2^{-k+1}\sum_{\mathcal{Y}(2^k)} \operatorname{vol}(xH)&\quad&\text{by the
definition of $\mathcal{Y}(2^k)$}\\
&\ll 2^{-k}\sum_{j=1}^{M} \sum_{C_v\subset z_j.{\rm Box}(\eta)} \operatorname{vol}(C_v)&\quad&\text{by (10.8)}\\
&\ll \alpha_s^{12/s}\sum_{j=1}^{R} 2^{{6k}/{s}-k} &\quad& \text{by (10.9)} \\
&\ll {\operatorname{Vol} (X)}\alpha_s^{12/s}2^{{6k}/{s}-k}&\quad&\text{since~$R=O(\operatorname{Vol}(X))$;}
\end{aligned}\end{align*}
in the above we also used the fact that ![]() $\operatorname {vol}(C_v)\ll _\rho 1$.
$\operatorname {vol}(C_v)\ll _\rho 1$.
Since ![]() $\rho \asymp \eta$ can be taken
$\rho \asymp \eta$ can be taken ![]() $\asymp {\varepsilon }_X^{k}$, we conclude that for some absolute constant
$\asymp {\varepsilon }_X^{k}$, we conclude that for some absolute constant ![]() $N_1, N_2\ge 1$ and
$N_1, N_2\ge 1$ and ![]() $c=c(s)\ge 1$,
$c=c(s)\ge 1$,
 \[ \mathcal{N}(T)\le c\, \operatorname{Vol} (X) \rho^{-N_1} \alpha_s^{12/s} \sum_{k=n_0}^{n_T} 2^{{6k}/{s}-k}\le c\, \operatorname{Vol} (X) {\varepsilon}_X^{-N_2} T^{{6}/{s}-1} \]
\[ \mathcal{N}(T)\le c\, \operatorname{Vol} (X) \rho^{-N_1} \alpha_s^{12/s} \sum_{k=n_0}^{n_T} 2^{{6k}/{s}-k}\le c\, \operatorname{Vol} (X) {\varepsilon}_X^{-N_2} T^{{6}/{s}-1} \]
which implies the claim (note here that ![]() $\operatorname {Vol} (X)=\operatorname {Vol} (M)$, since
$\operatorname {Vol} (X)=\operatorname {Vol} (M)$, since ![]() $\Gamma$ is torsion-free.)
$\Gamma$ is torsion-free.)
Remark 10.11 Let ![]() $\mathcal {N}_M(T)$ be the number of properly immersed geodesic planes of area at most
$\mathcal {N}_M(T)$ be the number of properly immersed geodesic planes of area at most ![]() $T$ in a general geometrically finite manifold
$T$ in a general geometrically finite manifold ![]() $M=\Gamma \backslash \mathbb {H}^3$. If
$M=\Gamma \backslash \mathbb {H}^3$. If ![]() $Y$ is a closed
$Y$ is a closed ![]() $H$-orbit
$H$-orbit ![]() $Y$ of finite area in
$Y$ of finite area in ![]() $\Gamma \backslash G$, then
$\Gamma \backslash G$, then ![]() $\mathsf {p}_Y\asymp \mathsf {s}_Y=2$,
$\mathsf {p}_Y\asymp \mathsf {s}_Y=2$, ![]() $\tau _Y=\operatorname {Vol} (Y)$ and the non-divergence of the
$\tau _Y=\operatorname {Vol} (Y)$ and the non-divergence of the ![]() $U$-action as given in [Reference Buenger and ZhengBZ17, Theorem 1.1] implies that (10.8) also holds in this setting.
$U$-action as given in [Reference Buenger and ZhengBZ17, Theorem 1.1] implies that (10.8) also holds in this setting.
In view of these, the proof of Corollary 10.7 works in the same way for the following: there exists ![]() $N\ge 1$ (depending only on
$N\ge 1$ (depending only on ![]() $G$) such that for any
$G$) such that for any ![]() $1/2< s<1$, we have
$1/2< s<1$, we have
where the implied constant depends only on ![]() $s$.
$s$.
Acknowledgements
A.M. would like to thank the Institute for Advanced Study for its hospitality during the fall of 2019 where some parts of this project were carried out. We would like to thank the referee for a careful reading of our paper and for making many useful comments.
Appendix A. Proof of Theorem 1.1 in the compact case
In this section we present the proof of Theorem 1.1 when ![]() $X$ is compact. As was mentioned in the introduction, this case is due to G. Margulis.
$X$ is compact. As was mentioned in the introduction, this case is due to G. Margulis.
Let ![]() $Y\neq Z$ be two closed
$Y\neq Z$ be two closed ![]() $H$-orbits in
$H$-orbits in ![]() $X=\Gamma \backslash G$. Recall
$X=\Gamma \backslash G$. Recall ![]() ${\varepsilon }_X=\min _{x\in X}\operatorname {inj}(x)$ where
${\varepsilon }_X=\min _{x\in X}\operatorname {inj}(x)$ where ![]() $\operatorname {inj}(x)$ is the injectivity radius measured in
$\operatorname {inj}(x)$ is the injectivity radius measured in ![]() $\Gamma \backslash \mathbb {H}^3$.
$\Gamma \backslash \mathbb {H}^3$.
Fix ![]() $0< s<1$, and define
$0< s<1$, and define ![]() $f_s:Y\to [2,\infty )$ as follows: for any
$f_s:Y\to [2,\infty )$ as follows: for any ![]() $y\in Y$,
$y\in Y$,
 \[ f_s(y)=\begin{cases} \sum_{v\in I_Z(y)}\|v\|^{-s} & \text{ if $I_Z(y)\neq\emptyset $,}\\ {\varepsilon}_X^{-s} & \text{otherwise,} \end{cases} \]
\[ f_s(y)=\begin{cases} \sum_{v\in I_Z(y)}\|v\|^{-s} & \text{ if $I_Z(y)\neq\emptyset $,}\\ {\varepsilon}_X^{-s} & \text{otherwise,} \end{cases} \]
where
Define ![]() $F_{s}=F_{s, Y, Z}:Y\to (0,\infty )$ as follows:
$F_{s}=F_{s, Y, Z}:Y\to (0,\infty )$ as follows:
Note that in the case at hand, ![]() $F_s$ is a bounded Borel function on
$F_s$ is a bounded Borel function on ![]() $Y$. We also note that in the case at hand
$Y$. We also note that in the case at hand ![]() $\omega$, as defined in (6.3), is a bounded function on
$\omega$, as defined in (6.3), is a bounded function on ![]() $X$ (recall that
$X$ (recall that ![]() $\omega =2$ in this case), and hence
$\omega =2$ in this case), and hence ![]() $F_s$ here and
$F_s$ here and ![]() $F_{s,\lambda _s}$ that we considered in the proof of Theorem 1.5 are essentially the same functions in this case.
$F_{s,\lambda _s}$ that we considered in the proof of Theorem 1.5 are essentially the same functions in this case.
We use the following special case of Lemma 5.6: for any ![]() $v\in i\mathfrak {sl}_2(\mathbb {R})$ with
$v\in i\mathfrak {sl}_2(\mathbb {R})$ with ![]() $\|v\|=1$,
$\|v\|=1$, ![]() $1/3\le s<1$ and
$1/3\le s<1$ and ![]() $t>0$, we have
$t>0$, we have
where ![]() $vh= \operatorname {Ad}(h) (v)$ for all
$vh= \operatorname {Ad}(h) (v)$ for all ![]() $h\in H$.
$h\in H$.
Remark A.2 It is worth noting that the symmetric interval ![]() $[-1,1]$ was used in Lemma 5.6. We remark that this is necessary in the infinite volume setting; indeed the half interval
$[-1,1]$ was used in Lemma 5.6. We remark that this is necessary in the infinite volume setting; indeed the half interval ![]() $[0,1]$ may even be a null set for
$[0,1]$ may even be a null set for ![]() $\mu _y$ for some
$\mu _y$ for some ![]() $y$; see (4.1) for the notation.
$y$; see (4.1) for the notation.
For a locally bounded function ![]() $\psi$ on
$\psi$ on ![]() $Y$ and
$Y$ and ![]() $t>0$, define
$t>0$, define
Proposition A.4 Let ![]() $1/3\le s<1$. There exists
$1/3\le s<1$. There exists ![]() $t=t(s)>0$ such that for all
$t=t(s)>0$ such that for all ![]() $y\in Y$,
$y\in Y$,
where ![]() $\alpha _s= (1-s)^{-1/(1-s)}$ and
$\alpha _s= (1-s)^{-1/(1-s)}$ and ![]() $c\ge 1$ is an absolute constant.
$c\ge 1$ is an absolute constant.
Proof. It suffices to show that ![]() ${\mathsf {A}}_t f_s(y)\leq \tfrac {1}{2}f_s(y)+ \alpha _s^4 {\rm Vol}(Z)$.
${\mathsf {A}}_t f_s(y)\leq \tfrac {1}{2}f_s(y)+ \alpha _s^4 {\rm Vol}(Z)$.
Let ![]() $b_0$ be as in (A.1), and let
$b_0$ be as in (A.1), and let ![]() $t=t(s)$ be given by the equation
$t=t(s)$ be given by the equation
We compare ![]() $f_s(yu_ra_t)$ and
$f_s(yu_ra_t)$ and ![]() $f_s(y)$ for
$f_s(y)$ for ![]() $r\in [0,1]$. Let
$r\in [0,1]$. Let ![]() $C_1\asymp e^{ t}$ be large enough so that
$C_1\asymp e^{ t}$ be large enough so that ![]() $\|vh\|\leq C_1\|v\|$ for all
$\|vh\|\leq C_1\|v\|$ for all ![]() $v\in i\frak {sl}_2(\mathbb {R})$ and all
$v\in i\frak {sl}_2(\mathbb {R})$ and all
Let ![]() $v\in I_Z(yu_ra_t)$ be so that
$v\in I_Z(yu_ra_t)$ be so that ![]() $\|v\|< {\varepsilon }_X/C_1$. Then
$\|v\|< {\varepsilon }_X/C_1$. Then ![]() $\|va_{-t}u_{-r}\|\leq {\varepsilon }_X$; in particular,
$\|va_{-t}u_{-r}\|\leq {\varepsilon }_X$; in particular, ![]() $va_{-t}u_{-r}\in I_Z(y)$.
$va_{-t}u_{-r}\in I_Z(y)$.
In the following, if ![]() $I_Z(\cdot )=\emptyset$, the sum is interpreted as to equal to
$I_Z(\cdot )=\emptyset$, the sum is interpreted as to equal to ![]() ${\varepsilon }_X^{-s}$. In view of the above observation and the definition of
${\varepsilon }_X^{-s}$. In view of the above observation and the definition of ![]() $f_s$, we have
$f_s$, we have
 \begin{align} f_s(yu_ra_t)&=\sum_{v\in I_Z(yu_ra_t)}\|v\|^{-s}\nonumber\\ &=\sum_{v\in I_Z(yu_ra_t), \|v\|< {\varepsilon}_X/C_1}\|v\|^{-s}+\sum_{v\in I_Z(yu_ra_t), \|v\|\geq {\varepsilon}_X/C_1}\|v\|^{-s}\nonumber\\ &\leq \sum_{v\in I_Z(y)}\|vu_ra_t\|^{-s}+\sum_{v\in I_Z(yu_ra_t), \|v\|\geq {\varepsilon}_X/C_1}\|v\|^{-s}. \end{align}
\begin{align} f_s(yu_ra_t)&=\sum_{v\in I_Z(yu_ra_t)}\|v\|^{-s}\nonumber\\ &=\sum_{v\in I_Z(yu_ra_t), \|v\|< {\varepsilon}_X/C_1}\|v\|^{-s}+\sum_{v\in I_Z(yu_ra_t), \|v\|\geq {\varepsilon}_X/C_1}\|v\|^{-s}\nonumber\\ &\leq \sum_{v\in I_Z(y)}\|vu_ra_t\|^{-s}+\sum_{v\in I_Z(yu_ra_t), \|v\|\geq {\varepsilon}_X/C_1}\|v\|^{-s}. \end{align}
Moreover, note that ![]() $\# I_Z(y)\ll {\varepsilon }_X^{-3} {\rm Vol}(Z)$ (see the proof of Lemma 8.13). Hence,
$\# I_Z(y)\ll {\varepsilon }_X^{-3} {\rm Vol}(Z)$ (see the proof of Lemma 8.13). Hence,
We now average (A.6) over ![]() $[0,1]$. Then using (A.7) and (A.1) we get
$[0,1]$. Then using (A.7) and (A.1) we get
As ![]() $(1-s)^{-1/(1-s)} \asymp e^{st/4}$, this proves (A.5).
$(1-s)^{-1/(1-s)} \asymp e^{st/4}$, this proves (A.5).
Let ![]() $m_Y$ be the
$m_Y$ be the ![]() $H$-invariant probability measure on
$H$-invariant probability measure on ![]() $Y$.
$Y$.
Corollary A.8 We have
where ![]() $c\ge 1$ is an absolute constant.
$c\ge 1$ is an absolute constant.
Proof. Since ![]() $m_Y$ is an
$m_Y$ is an ![]() $H$-invariant probability measure,
$H$-invariant probability measure, ![]() $m_Y({\mathsf {A}}_t f_s)=m_Y(f_s)$. Hence the claim follows by integrating (A.5) with respect to
$m_Y({\mathsf {A}}_t f_s)=m_Y(f_s)$. Hence the claim follows by integrating (A.5) with respect to ![]() $m_Y$.
$m_Y$.
Proof of Theorem 1.1 There exists ![]() $\sigma >0$ such that for any
$\sigma >0$ such that for any ![]() $h\in B_H({\varepsilon }_X)$ and
$h\in B_H({\varepsilon }_X)$ and ![]() $y\in Y$,
$y\in Y$, ![]() $F_s(y)\le \sigma F_s(yh)$ (cf. Lemma 9.10);
$F_s(y)\le \sigma F_s(yh)$ (cf. Lemma 9.10); ![]() $B_H({\varepsilon }_X)$ denotes the
$B_H({\varepsilon }_X)$ denotes the ![]() ${\varepsilon }_X$-ball centered at the identity in
${\varepsilon }_X$-ball centered at the identity in ![]() $H$.
$H$.
Hence, using Corollary A.8, we deduce
 \begin{align*} f_s(y) &\le F_s(y)\le \frac{\sigma\int_{B_H( {\varepsilon}_X)} F_s (yh) \,dm_Y(yh)}{m_Y(B(y, {\varepsilon}_X))}\\ &\le \frac{\sigma\cdot{m_Y(F_s)} }{m_Y(B(y, {\varepsilon}_X))} \ll \alpha_s^4 {\varepsilon}_X^{-7} \operatorname{Vol}(Y) \operatorname{Vol}(Z) \end{align*}
\begin{align*} f_s(y) &\le F_s(y)\le \frac{\sigma\int_{B_H( {\varepsilon}_X)} F_s (yh) \,dm_Y(yh)}{m_Y(B(y, {\varepsilon}_X))}\\ &\le \frac{\sigma\cdot{m_Y(F_s)} }{m_Y(B(y, {\varepsilon}_X))} \ll \alpha_s^4 {\varepsilon}_X^{-7} \operatorname{Vol}(Y) \operatorname{Vol}(Z) \end{align*}
with an absolute implied constant. Since ![]() $d(y, Z)^{-s}\le c_1 f_s(y)$ for an absolute constant
$d(y, Z)^{-s}\le c_1 f_s(y)$ for an absolute constant ![]() $c_1\ge 1$ (see (10.4)), we have
$c_1\ge 1$ (see (10.4)), we have
This shows Theorem 1.1(1). By Corollary A.8 and the Chebyshev inequality, we get
Therefore
which implies Theorem 1.1(2).