If the ratio m/p tends to zero, where m is the number of factors m and m the number of observable variables, then the inverse diagonal element of the inverted observable covariance matrix 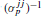 tends to the corresponding unique variance ψjj for almost all of these (Guttman, 1956). If the smallest singular value of the loadings matrix from Common Factor Analysis tends to infinity as p increases, then m/p tends to zero. The same condition is necessary and sufficient for
tends to the corresponding unique variance ψjj for almost all of these (Guttman, 1956). If the smallest singular value of the loadings matrix from Common Factor Analysis tends to infinity as p increases, then m/p tends to zero. The same condition is necessary and sufficient for 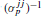 to tend to ψjj for all of these. Several related conditions are discussed.
to tend to ψjj for all of these. Several related conditions are discussed.