Hostname: page-component-5f745c7db-j9pcf Total loading time: 0 Render date: 2025-01-06T23:13:23.548Z Has data issue: true hasContentIssue false
  • English
  • Français

Convergence of Estimates of Unique Variances in Factor Analysis, Based on the Inverse Sample Covariance Matrix

Published online by Cambridge University Press:  01 January 2025

Wim P. Krijnen
Wim P. Krijnen*
Affiliation:
University of Amsterdam
*
Requests for reprints should be sent to W.P. Krijnen, Department of Psychology, Psychological Methods, University of Amsterdam, Roetersstraat 15, 1018 WB Amsterdam, The Netherlands.
Get access Rights & Permissions [Opens in a new window]

Abstract

If the ratio m/p tends to zero, where m is the number of factors m and m the number of observable variables, then the inverse diagonal element of the inverted observable covariance matrix 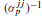tends to the corresponding unique variance ψjj for almost all of these (Guttman, 1956). If the smallest singular value of the loadings matrix from Common Factor Analysis tends to infinity as p increases, then m/p tends to zero. The same condition is necessary and sufficient for 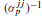to tend to ψjj for all of these. Several related conditions are discussed.

Keywords

common factor analysisconfirmatory factor analysisimage factor analysis
Type
Original Paper
Information
Psychometrika , Volume 71 , Issue 1 , March 2006 , pp. 193 - 199
Copyright
Copyright © 2006 The Psychometric Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is obliged Jos Ten Berge for his comments on the final draft and to the associate editor and the reviewers for their stimulating remarks during the review process.

References

Bekker, P.A., & Ten Berge, J.M.F. (1996). Generic global identification in factor analysis. Linear Algebra and its Applications, 264, 255–263.CrossRefGoogle Scholar
Bellman, R. (1960). Introduction to matrix analysis, New York: McGraw-Hill.Google Scholar
Billingsley, P. (1995). Probability and measure, (3rd ed.). New York: Wiley.Google Scholar
Guttman, L. (1956). Best possible systematic estimates of communalities. Psychometrika, 21, 273–285.CrossRefGoogle Scholar
Hayashi, K., & Bentler, P.M. (2000). On the relations among regular, equal unique variances and image factor analysis. Psychometrika, 65, 59–72.CrossRefGoogle Scholar
Henderson, H.V., & Searle, S.R. (1981). On deriving the inverse of a sum of matrices. SIAM Review, 23, 53–60.CrossRefGoogle Scholar
Horn, R.A., & Johnson, C.R. (1985). Matrix analysis, Cambridge, UK: Cambridge University Press.CrossRefGoogle Scholar
Jöreskog, K.G. (1967). Some contributions to maximum likelihood factor analysis. Psychometrika, 32, 443–482.CrossRefGoogle Scholar
Lipschutz, S. (1965). General topology, New York: McGraw-Hill.Google Scholar
Rudin, W. (1976). Principles of mathematical analysis, (3rd ed.). New York: McGraw-Hill.Google Scholar
Schneeweiss, H. (1997). Factors and principal components in the near spherical case. Multivariate Behavioural Research, 32, 375–401.CrossRefGoogle ScholarPubMed
Shapiro, A. (1982). Rank-reducibility of a symmetric matrix and sampling theory of minimum trace factor analysis. Psychometrika, 47, 187–199.CrossRefGoogle Scholar
Styan, G.P.H. (1973). Hadamard products and multivariate statistical analysis. Linear Algebra and its Applications, 6, 217–240.CrossRefGoogle Scholar