Alfred Schild established conditions where Lorentz transformations map world-vectors
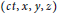 $\left( ct,\,x,\,y,\,z \right)$
with integer coordinates onto vectors of the same kind. The problem was dealt with in the context of tensor and spinor calculus. Due to Schild’s number-theoretic arguments, the subject is also interesting when isolated from its physical background.
$\left( ct,\,x,\,y,\,z \right)$
with integer coordinates onto vectors of the same kind. The problem was dealt with in the context of tensor and spinor calculus. Due to Schild’s number-theoretic arguments, the subject is also interesting when isolated from its physical background.
Schild’s paper is not easy to understand. Therefore, we first present a streamlined version of his proof which is based on the use of null vectors. Then we present a purely algebraic proof that is somewhat shorter. Both proofs rely on the properties of Gaussian integers