3 results
EXTENSIONS OF AUTOCORRELATION INEQUALITIES WITH APPLICATIONS TO ADDITIVE COMBINATORICS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 08 April 2020, pp. 451-461
- Print publication:
- December 2020
-
- Article
- Export citation
-
Barnard and Steinerberger [‘Three convolution inequalities on the real line with connections to additive combinatorics’, Preprint, 2019, arXiv:1903.08731] established the autocorrelation inequality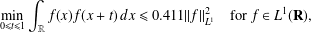
where the constant
$$\begin{eqnarray}\min _{0\leq t\leq 1}\int _{\mathbb{R}}f(x)f(x+t)\,dx\leq 0.411||f||_{L^{1}}^{2}\quad \text{for}~f\in L^{1}(\mathbf{R}),\end{eqnarray}$$
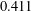$0.411$ cannot be replaced by 
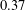$0.37$. In addition to being interesting and important in their own right, inequalities such as these have applications in additive combinatorics. We show that for 
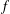$f$ to be extremal for this inequality, we must have Our central technique for deriving this result is local perturbation of
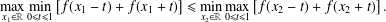$$\begin{eqnarray}\max _{x_{1}\in \mathbb{R}}\min _{0\leq t\leq 1}\left[f(x_{1}-t)+f(x_{1}+t)\right]\leq \min _{x_{2}\in \mathbb{R}}\max _{0\leq t\leq 1}\left[f(x_{2}-t)+f(x_{2}+t)\right].\end{eqnarray}$$
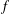$f$ to increase the value of the autocorrelation, while leaving 
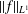$||f||_{L^{1}}$ unchanged. These perturbation methods can be extended to examine a more general notion of autocorrelation. Let 
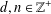$d,n\in \mathbb{Z}^{+}$, 
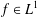$f\in L^{1}$, 
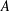$A$ be a 
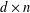$d\times n$ matrix with real entries and columns 
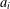$a_{i}$ for 
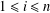$1\leq i\leq n$ and 
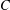$C$ be a constant. For a broad class of matrices 
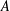$A$, we prove necessary conditions for 
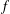$f$ to extremise autocorrelation inequalities of the form 
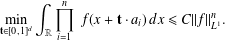$$\begin{eqnarray}\min _{\mathbf{t}\in [0,1]^{d}}\int _{\mathbb{R}}\mathop{\prod }_{i=1}^{n}~f(x+\mathbf{t}\cdot a_{i})\,dx\leq C||f||_{L^{1}}^{n}.\end{eqnarray}$$
Weighted norm inequalities for positive operators restricted on the cone of λ-quasiconcave functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 17-39
- Print publication:
- February 2020
-
- Article
- Export citation
-
Let ρ be a monotone quasinorm defined on
${\rm {\frak M}}^ + $, the set of all non-negative measurable functions on [0, ∞). Let T be a monotone quasilinear operator on 
${\rm {\frak M}}^ + $. We show that the following inequality restricted on the cone of λ-quasiconcave functions
where
$$\rho (Tf) \les C_1\left( {\int_0^\infty {f^p} v} \right)^{1/p},$$
$1\les p\les \infty $ and v is a weighted function, is equivalent to slightly different inequalities considered for all non-negative measurable functions. The case 0 < p < 1 is also studied for quasinorms and operators with additional properties. These results in turn enable us to establish necessary and sufficient conditions on the weights (u, v, w) for which the three weighted Hardy-type inequality
holds for all λ-quasiconcave functions and all 0 < p, q ⩽ ∞.
$$\left( {\int_0^\infty {{\left( {\int_0^x f u} \right)}^q} w(x){\rm d}x} \right)^{1/q} \les C_1\left( {\int_0^\infty {f^p} v} \right)^{1/p},$$
Well posedness and control of semilinear wave equations with iterated logarithms
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 4 / 1999
- Published online by Cambridge University Press:
- 15 August 2002, pp. 37-56
- Print publication:
- 1999
-
- Article
- Export citation
