Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T16:58:09.018Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted norm inequalities for positive operators restricted on the cone of λ-quasiconcave functions

Part of: Inequalities

Published online by Cambridge University Press:  23 January 2019

Amiran Gogatishvili  and
Júlio S. Neves
Amiran Gogatishvili
Affiliation:
Institute of Mathematics of the Czech Academy of Sciences, Žitna 25, 11567 Praha 1, Czech Republic (gogatish@math.cas.cz)
Júlio S. Neves
Affiliation:
CMUC, Department of Mathematics, University of Coimbra, Apartado 3008, EC Santa Cruz, 3001–454 Coimbra, Portugal (jsn@mat.uc.pt)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let ρ be a monotone quasinorm defined on 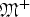${\rm {\frak M}}^ + $, the set of all non-negative measurable functions on [0, ∞). Let T be a monotone quasilinear operator on 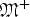${\rm {\frak M}}^ + $. We show that the following inequality restricted on the cone of λ-quasiconcave functions

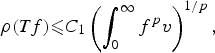$$\rho (Tf) \les C_1\left( {\int_0^\infty {f^p} v} \right)^{1/p},$$
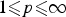where $1\les p\les \infty $ and v is a weighted function, is equivalent to slightly different inequalities considered for all non-negative measurable functions. The case 0 < p < 1 is also studied for quasinorms and operators with additional properties. These results in turn enable us to establish necessary and sufficient conditions on the weights (u, v, w) for which the three weighted Hardy-type inequality
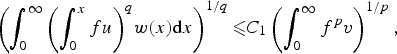$$\left( {\int_0^\infty {{\left( {\int_0^x f u} \right)}^q} w(x){\rm d}x} \right)^{1/q} \les C_1\left( {\int_0^\infty {f^p} v} \right)^{1/p},$$
holds for all λ-quasiconcave functions and all 0 < p, q ⩽ ∞.

Keywords

Quasilinear operatorintegral inequalityLebesgue spaceweightHardy operatorquasiconcave functionsmonotone functions

MSC classification

Primary: 26D10: Inequalities involving derivatives and differential and integral operators
Secondary: 26D15: Inequalities for sums, series and integrals 26D07: Inequalities involving other types of functions
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 1 , February 2020 , pp. 17 - 39
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ariño, M. A. and Muckenhoupt, B.. Maximal functions on classical Lorentz spaces and Hardy's inequality with weights for nonincreasing functions. Trans. Amer. Math. Soc. 320 (1990), 727–735.Google Scholar
2Bennett, C. and Sharpley, R.. Interpolation of operators, vol. 129, Pure and applied Mathematics (Boston, MA: Academic Press Inc., 1988).Google Scholar
3Bergh, J. and Löfström, J.. Interpolation spaces. An introduction. Grundlehren der Mathematischen Wissenschaften,vol. 223 (Berlin-New York: Springer-Verlag, 1976).CrossRefGoogle Scholar
4Bergh, J., Burenkov, V. and Persson, L.-E.. Best constants in reversed Hardy's inequalities for quasimonotone functions. Acta Sci. Math. (Szeged) 59 (1994), 221–239.Google Scholar
5Brudnyi, Y. and Shteinberg, A.. Calderón couples of Lipschitz spaces. J. Funct. Anal.. 131 (1995), 459–498.CrossRefGoogle Scholar
6Caetano, A. M., Gogatishvili, A. and Opic, B.. Sharp embeddings of Besov spaces involving only logarithmic smoothness. J. Approx. Theory 152 (2008), 188–214.CrossRefGoogle Scholar
7Caetano, A. M., Gogatishvili, A. and Opic, B.. Embeddings and the growth envelope of Besov spaces involving only slowly varying smoothness. J. Approx. Theory 163 (2011), 1373–1399.CrossRefGoogle Scholar
8Carro, M. J., Raposo, J. A. and Soria, J.. Recent developments in the theory of Lorentz spaces and weighted inequalities. Mem. Amer. Math. Soc. 187 (2007), xii+128.Google Scholar
9Gogatishvili, A. and Kerman, R.. The rearrangement-invariant space Γp,ϕ. Positivity 18 (2014), 319–345.CrossRefGoogle Scholar
10Gogatishvili, A. and Pick, L.. Discretization and anti-discretization of rearrangement-invariant norms. Publ. Mat. 47 (2003), 311–358.CrossRefGoogle Scholar
11Gogatishvili, A. and Pick, L.. Embeddings and duality theorems for weak classical Lorentz spaces. Canad. Math. Bull. 49 (2006), 82–95.CrossRefGoogle Scholar
12Gogatishvili, A. and Stepanov, V. D.. Reduction theorems for operators on the cones of monotone functions. J. Math. Anal. Appl. 405 (2013a), 156–172.CrossRefGoogle Scholar
13Gogatishvili, A. and Stepanov, V. D.. Reduction theorems for weighted integral inequalities on the cone of monotone functions. Uspekhi Mat. Nauk 68 (2013b), 3–68, [translation in Russian Math. Surveys 68 (2013), no. 4, 597–664].Google Scholar
14Gogatishvili, A., Neves, J. S. and Opic, B.. Optimality of embeddings of Bessel-potential-type spaces into Lorentz-Karamata spaces. Proc. Roy. Soc. Edinburgh Sect. A 134 (2004), 1127–1147.CrossRefGoogle Scholar
15Gogatishvili, A., Kufner, A. and Persson, L.-E.. Some new scales of weight characterizations of the class B p. Acta Math. Hungar. 123 (2009a), 365–377.CrossRefGoogle Scholar
16Gogatishvili, A., Neves, J. S. and Opic, B.. Optimal embeddings and compact embeddings of Bessel-potential-type spaces. Math. Z. 262 (2009b), 645–682.CrossRefGoogle Scholar
17Gogatishvili, A., Opic, B., Tikhonov, S. and Trebels, W.. Ulyanov-type inequalities between Lorentz-Zygmund spaces. J. Fourier Anal. Appl. 20 (2014), 1020–1049.CrossRefGoogle Scholar
18Gol′dman, M. L.. Integral inequalities on a cone of functions with monotonicity properties. Dokl. Akad. Nauk SSSR 320 (1991), 1037–1042, [translation in Soviet Math. Dokl. 44 (1992), no. 2, 581–587].Google Scholar
19Gol′dman, M. L.. On integral inequalities on the set of functions with some properties of monotonicity. In Function spaces, differential operators and nonlinear analysis (Friedrichroda, 1992), volume 133 of Teubner-Texte Math.,pp. 274–279 (Stuttgart: Teubner, 1993).CrossRefGoogle Scholar
20Gol′dman, M. L.. On optimal embeddings of generalized Bessel and Riesz potentials. Tr. Mat. Inst. Steklova, 269 (2010), 91–111, [translation in Proc. Steklov Inst. Math. 269 (2010), no. 1, 85–105].Google Scholar
21Gol′dman, M. L. and Haroske, D. D.. Estimates for continuity envelopes and approximation numbers of Bessel potentials. J. Approx. Theory 172 (2013), 58–85.CrossRefGoogle Scholar
22Gol′dman, M. L. and Kerman, R. A.. On the optimal embedding of Calderón spaces and of generalized Besov spaces. In Function Spaces, Approximations, and Differential Equations, Collected papers dedicated to Oleg Vladimirovich Besov on his 70th birthday,vol. 243,pp. 161–193 (Moscow: Nauka, 2003), [translation in Proc. Steklov Inst. Math. 2003, no. 4 (243), 154–184].Google Scholar
23Gol′dman, M. L., Heinig, H. P. and Stepanov, V. D.. On the principle of duality in Lorentz spaces. Canad. J. Math. 48 (1996), 959–979.CrossRefGoogle Scholar
24Haroske, D. D.. Envelopes and sharp embeddings of function spaces Chapman & Hall/CRC Research Notes in Mathematics, vol. 437 (Boca Raton, FL: Chapman & Hall/CRC, 2007).Google Scholar
25Heinig, H. and Maligranda, L.. Weighted inequalities for monotone and concave functions. Studia Math. 116 (1995), 133–165.Google Scholar
26Kufner, A. and Persson, L.-E.. Weighted inequalities of Hardy type (River Edge, NJ: World Scientific Publishing Co., Inc., 2003).CrossRefGoogle Scholar
27Křepela, M.. Boundedness of Hardy-type operators with a kernel: integral weighted conditions for the case $0<q<1\les p<\infty $. Rev. Mat. Complut. 30 (2017), 547–587.CrossRefGoogle Scholar
28Maligranda, L.. Weighted inequalities for quasi-monotone functions. J. London Math. Soc. (2) 57 (1998), 363–370.CrossRefGoogle Scholar
29Oĭnarov, R.. Two-sided estimates for the norm of some classes of integral operators. Trudy Mat. Inst. Steklov. 204, 240–250 (1993), (Issled. po Teor. Differ. Funktsii Mnogikh Peremen. i ee Prilozh. 16). [translation in Proc. Steklov Inst. Math. 1994, no. 3 (204), 205–214].Google Scholar
30Ovchinnikov, V. I.. Interpolation functions and the Lions-Peetre interpolation construction. Uspekhi Mat. Nauk, 69 (2014), 103–168, [translation in Russian Math. Surveys 69 (2014), no. 4, 681–741].Google Scholar
31Persson, L.-E., Popova, O. V. and Stepanov, V. D.. Weighted Hardy-type inequalities on the cone of quasi-concave functions. Math. Inequal. Appl. 17 (2014), 879–898.Google Scholar
32Persson, L.-E., Shambilova, G. E. and Stepanov, V. D.. Hardy-type inequalities on the weighted cones of quasi-concave functions. Banach J. Math. Anal. 9 (2015), 21–34.CrossRefGoogle Scholar
33Sawyer, E.. Boundedness of classical operators on classical Lorentz spaces. Studia Math. 96 (1990), 145–158.CrossRefGoogle Scholar
34Sinnamon, G.. Embeddings of concave functions and duals of Lorentz spaces. Publ. Mat. 46 (2002), 489–515.CrossRefGoogle Scholar
35Sinnamon, G. and Stepanov, V. D.. The weighted Hardy inequality: new proofs and the case p = 1. J. London Math. Soc. (2) 54 (1996), 89–101.CrossRefGoogle Scholar
36Stepanov, V. D.. Weighted inequalities for a class of Volterra convolution operators. J. London Math. Soc. (2) 45 (1992), 232–242.CrossRefGoogle Scholar
37Stepanov, V. D.. Integral operators on the cone of monotone functions. J. London Math. Soc. (2) 48 (1993), 465–487.CrossRefGoogle Scholar
38Stepanov, V. D.. Weighted norm inequalities of Hardy type for a class of integral operators. J. London Math. Soc. (2) 50 (1994), 105–120.CrossRefGoogle Scholar
39Stepanov, V. D.. On optimal Banach spaces containing a weight cone of monotone or quasiconcave functions. Mat. Zametki 98 (2015), 907–922, [translation in Math. Notes 98 (2015), no. 5–6, 957–970].Google Scholar