For $f$ analytic in the unit disk $\mathbb{D}$, we consider the close-to-convex analogue of a class of starlike functions introduced by R. Singh [‘On a class of star-like functions’, Compos. Math.19(1) (1968), 78–82]. This class of functions is defined by $|zf^{\prime }(z)/g(z)-1|<1$ for $z\in \mathbb{D}$, where $g$ is starlike in $\mathbb{D}$. Coefficient and other results are obtained for this class of functions.

If $B$ is the Blachke product with zeros 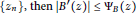$\{{{z}_{n}}\},\,\text{then}\,\left| {B}'\left( z \right) \right|\,\le \,{{\Psi }_{B}}\left( z \right)$, where

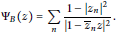$${{\Psi }_{B}}\,=\,\sum\limits_{n}{\frac{1-{{\left| {{z}_{n}} \right|}^{2}}}{{{\left| 1-{{\overline{z}}_{n}}z \right|}^{2}}}.}$$

Moreover, it is a well-known fact that, for 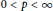$0\,<\,p\,<\,\infty $,

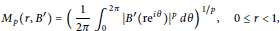$${{M}_{p\left( r,{B}' \right)}}\,=\,{{\left( \frac{1}{2\pi }\,\int_{0}^{2\pi }{{{\left| {B}'\left( \text{r}{{\text{e}}^{i\theta }} \right) \right|}^{p}}d\theta } \right)}^{{1}/{p}\;}},\,0\,\le \,r\,<\,1,$$

is bounded if and only if 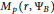${{M}_{p}}\left( r,\,{{\Psi }_{B}} \right)$ is bounded. We find a Blaschke product 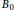${{B}_{0}}$ such that 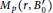${{M}_{p}}\left( r,\,{{{{B}'}}_{0}} \right)$ and 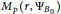${{M}_{p}}\left( r,{{\Psi }_{{{B}_{0}}}} \right)$ are not comparable for any 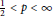$\frac{1}{2}\,<\,p\,<\,\infty $. In addition, it is shown that, if 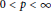$0\,<\,p\,<\,\infty$, $B$ is a Carleson-Newman Blaschke product and a weight $\omega $ satisfies a certain regularity condition, then

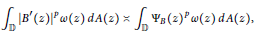$${{\int }_{\mathbb{D}}}{{\left| {B}'\left( z \right) \right|}^{p}}\omega \left( z \right)dA\left( z \right)~\asymp {{\int }_{\mathbb{D}}}{{\Psi }_{B}}{{\left( z \right)}^{p}}\omega \left( z \right)dA\left( z \right),$$

where 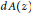$d\,A\left( z \right)$ is the Lebesgue area measure on the unit disc.