Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T08:58:32.339Z Has data issue: false hasContentIssue false
  • English
  • Français

Remark on Integral Means of Derivatives of Blaschke Products

Published online by Cambridge University Press:  20 November 2018

Atte Reijonen
Atte Reijonen*
Affiliation:
Department of Physics and Mathematics, University of Eastern Finland, P.O.Box 111, FI-80101 Joensuu, Finland, e-mail : atte.reijonen@uef.fi
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If $B$ is the Blachke product with zeros 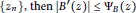$\{{{z}_{n}}\},\,\text{then}\,\left| {B}'\left( z \right) \right|\,\le \,{{\Psi }_{B}}\left( z \right)$, where

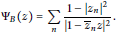$${{\Psi }_{B}}\,=\,\sum\limits_{n}{\frac{1-{{\left| {{z}_{n}} \right|}^{2}}}{{{\left| 1-{{\overline{z}}_{n}}z \right|}^{2}}}.}$$

Moreover, it is a well-known fact that, for 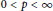$0\,<\,p\,<\,\infty $,

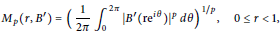$${{M}_{p\left( r,{B}' \right)}}\,=\,{{\left( \frac{1}{2\pi }\,\int_{0}^{2\pi }{{{\left| {B}'\left( \text{r}{{\text{e}}^{i\theta }} \right) \right|}^{p}}d\theta } \right)}^{{1}/{p}\;}},\,0\,\le \,r\,<\,1,$$

is bounded if and only if 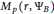${{M}_{p}}\left( r,\,{{\Psi }_{B}} \right)$ is bounded. We find a Blaschke product 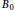${{B}_{0}}$ such that 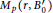${{M}_{p}}\left( r,\,{{{{B}'}}_{0}} \right)$ and 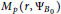${{M}_{p}}\left( r,{{\Psi }_{{{B}_{0}}}} \right)$ are not comparable for any 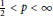$\frac{1}{2}\,<\,p\,<\,\infty $. In addition, it is shown that, if 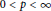$0\,<\,p\,<\,\infty$, $B$ is a Carleson-Newman Blaschke product and a weight $\omega $ satisfies a certain regularity condition, then

$${{\int }_{\mathbb{D}}}{{\left| {B}'\left( z \right) \right|}^{p}}\omega \left( z \right)dA\left( z \right)~\asymp {{\int }_{\mathbb{D}}}{{\Psi }_{B}}{{\left( z \right)}^{p}}\omega \left( z \right)dA\left( z \right),$$

where 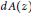$d\,A\left( z \right)$ is the Lebesgue area measure on the unit disc.

Keywords

30J1030H1030H20Bergman spaceBlaschke productHardy spaceintegral mean
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 3 , 01 September 2018 , pp. 640 - 649
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Ahern, P. R. and Clark, D. N., On inner functions with HP derivative. Michigan Math. J. 21 (1974), 115–127. http://dx.doi.Org/10.1307/mmj71 0290012 55Google Scholar
[2] Colwell, P., Blaschke products: Bounded analytic functions. University of Michigan Press, Ann Arbor, MI, 1985.Google Scholar
[3] Duren, P. L., Theory of HP Spaces. Pure and Applied Mathematics, 38, Academic Press, New York-London, 1970.Google Scholar
[4] Flett, T. M., The dual ofan inequaüty of Hardy and Littlewood and some related inequaüties. J. Math. Anal. Appl. 38 (1972), 746–765. http://dx.doi.Org/10.1016/0022-247X(72)90081-9Google Scholar
[5] Frostman, O., Sur les produits de Blaschke. Kungl. Fysiografiska Sällskapets i Lund Förhandlingar [Proc. Roy. Physiog. Soc. Lund] 12(1942), no. 15, 169–182.Google Scholar
[6] Garnett, J. B., Bounded analytic functions. Revised first edition, Graduate Texts in Mathematics, 236, Springer, New York, 2007.Google Scholar
[7] Girela, D. and Peläez, J. A., On the membership in Bergman Spaces of the derivative of a Blaschke product with zeros in a Stolz domain. Canad. Math. Bull. 49 (2006), no. 3, 381–388. http://dx.doi.Org/10.4153/CMB-2006-038-XGoogle Scholar
[8] Girela, D., Peläez, J. A., and Vukotic, D., Integrability ofthe derivative ofa Blaschke product. Proc. Edinb. Math. Soc. (2) 50 (2007), no. 3, 673–687. http://dx.doi.Org/10.1017/S0013091504001014Google Scholar
[9] Gluchoff, A., The mean modulus ofa Blaschke product with zeroes in a nontangential region. Complex Variables Theory Appl. 1 (1983), no. 4, 311–326. http://dx.doi.Org/10.1080/17476938308814022Google Scholar
[10] Hedenmalm, H., Korenblum, B., and Zhu, K., Theory of Bergman Spaces. Graduate Texts in Mathematics, 199, Springer-Verlag, New York, 2000. http://dx.doi.Org/10.1007/978-1-4612-0497-8Google Scholar
[11] Kim, H. O., Derivatives of Blaschke products. Pacific J. Math. 114(1984), no. 1, 175–190. http://dx.doi.Org/10.2140/pjm.1984.114.175Google Scholar
[12] Mashreghi, J., Derivatives of inner functions. Fields Institute Monographs, 31, Springer, New York; Fields Institute for Research in Mathematical Sciences, Toronto, ON, 2013.Google Scholar
[13] McDonald, G. and Sundberg, C., Toeplitz Operators on the disc. Indiana Univ. Math. J. 28 (1979), no. 4, 595–611. http://dx.doi.org/10.1512/iumj.1979.28.28042Google Scholar
[14] Peläez, J. A., Sharp results on the integrability ofthe derivative ofan interpolating Blaschkeproduct. Forum Math. 20 (2008), no. 6, 1039–1054. http://dx.doi.org/10.1515/FORUM.2008.046Google Scholar
[15] Peläez, J. A. and Rättyä, J., Embedding theorems for Bergman Spaces via harmonic analysis. Math. Ann. 362(2015), no. 1-2, 205–239. http://dx.doi.org/10.1007/s00208-014-1108-5Google Scholar
[16] Perez-Gonzälez, F. and Rättyä, J., Derivatives of inner functions in weighted Bergman Spaces and the Schwarz-Pick lemma. Proc. Amer. Math. Soc. 145 (2017), no. 5, 2155–2166. http://dx.doi.org/10.1090/proc/13384Google Scholar
[17] Perez-Gonzälez, F. and Rättyä, J., Inner functions in the Möbius invariant Besov-type Spaces. Proc. Edinb. Math. Soc. (2) 52 (2009), no. 3, 751–770. http://dx.doi.Org/10.1017/S001309150700081 8Google Scholar
[18] Perez-Gonzälez, F., Rättyä, J., and Reijonen, A., Derivatives of inner functions in Bergman Spaces induced by doubling weights. Ann. Acad. Sei. Fenn. Math. 42 (2017), 735–753. http://dx.doi.Org/10.5186/aasfm.2O17.4248Google Scholar
[19] Protas, D., Blaschke produets with derivative infunetion Spaces. Kodai Math. J. 34 (2011), no. 1, 124–131. http://dx.doi.org/10.2996/kmj71301576766Google Scholar
[20] Reijonen, A., Derivatives of Blaschke produets whose zeros lie in a Stolz domain and weighted Bergman Spaces. Proc. Amer. Math. Soc, to appear.Google Scholar
[21] Shapiro, J. H., Composition Operators and classical funetion theory. Universitext: Tracts in Mathematics, Springer-Verlag, New York, 1993. http://dx.doi.Org/10.1007/978-1-4612-0887-7Google Scholar
[22] Vinogradov, S. A., Multiplication and division in the Space of analytic functions with an area-integrable derivative, and in some related Spaces (Russian). Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 222(1995), Issled, po Linein. Oper, i Teor. Funktsii 23, 45-77; J. Math. Sei. (New York) 87 (1997), no. 5, 3806–3827. http://dx.doi.org/10.1007/BF02355826Google Scholar