This paper addresses the problem of constructing a cycle-level intersection theory for toric varieties. We show that by making one global choice, we can determine a cycle representative for the intersection of an equivariant Cartier divisor with an invariant cycle on a toric variety. For a toric variety defined by a fan in 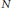 $N$, the choice consists of giving an inner product or a complete flag for
$N$, the choice consists of giving an inner product or a complete flag for
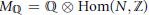 ${{M}_{\mathbb{Q}}}\,=\,\mathbb{Q}\,\otimes \,\text{Hom(}N,\,\mathbb{Z}\text{)}$
, or more generally giving for each cone σ in the fan a linear subspace of
${{M}_{\mathbb{Q}}}\,=\,\mathbb{Q}\,\otimes \,\text{Hom(}N,\,\mathbb{Z}\text{)}$
, or more generally giving for each cone σ in the fan a linear subspace of
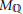 ${{M}_{\mathbb{Q}}}$
complementary to
${{M}_{\mathbb{Q}}}$
complementary to
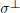 ${{\sigma }^{\bot }}$
, satisfying certain compatibility conditions. We show that these intersection cycles have properties analogous to the usual intersections modulo rational equivalence. If
${{\sigma }^{\bot }}$
, satisfying certain compatibility conditions. We show that these intersection cycles have properties analogous to the usual intersections modulo rational equivalence. If 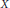 $X$ is simplicial (for instance, if
$X$ is simplicial (for instance, if 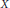 $X$ is non-singular), we obtain a commutative ring structure to the invariant cycles of
$X$ is non-singular), we obtain a commutative ring structure to the invariant cycles of 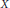 $X$ with rational coefficients. This ring structure determines cycles representing certain characteristic classes of the toric variety. We also discuss how to define intersection cycles that require no choices, at the expense of increasing the size of the coefficient field.
$X$ with rational coefficients. This ring structure determines cycles representing certain characteristic classes of the toric variety. We also discuss how to define intersection cycles that require no choices, at the expense of increasing the size of the coefficient field.
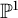 $\mathbb {P}^1$
$\mathbb {P}^1$
