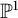1 Introduction
Let
![]() $\overline {\mathcal {M}}_{g,n}$
be the moduli space of n-pointed genus g stable curves. It is a proper smooth Deligne Mumford (DM) stack of dimension
$\overline {\mathcal {M}}_{g,n}$
be the moduli space of n-pointed genus g stable curves. It is a proper smooth Deligne Mumford (DM) stack of dimension
![]() $3g-3+n$
. We denote by
$3g-3+n$
. We denote by
![]() $\pi :\overline {\mathcal {C}}_{g,n}\to \overline {\mathcal {M}}_{g,n}$
the universal curve and by
$\pi :\overline {\mathcal {C}}_{g,n}\to \overline {\mathcal {M}}_{g,n}$
the universal curve and by
![]() $\sigma _i: \overline {\mathcal {M}}_{g,n}\to \overline {\mathcal {C}}_{g,n}$
the sections associated with the marking i for all
$\sigma _i: \overline {\mathcal {M}}_{g,n}\to \overline {\mathcal {C}}_{g,n}$
the sections associated with the marking i for all
![]() $1\leq i\leq n$
. We denote by
$1\leq i\leq n$
. We denote by
![]() $\omega _{\overline {\mathcal {C}}_{g,n}/ \overline {\mathcal {M}}_{g,n}}$
the relative dualizing sheaf of
$\omega _{\overline {\mathcal {C}}_{g,n}/ \overline {\mathcal {M}}_{g,n}}$
the relative dualizing sheaf of
![]() $\pi $
. We will consider the following classes in
$\pi $
. We will consider the following classes in
![]() $A^*(\overline {\mathcal {M}}_{g,n})$
:
$A^*(\overline {\mathcal {M}}_{g,n})$
:
-
• For all
 $0\leq i\leq g$
,
$0\leq i\leq g$
,
 $\lambda _i$
stands for the ith Chern class of the Hodge bundle, i.e., the vector bundle
$\lambda _i$
stands for the ith Chern class of the Hodge bundle, i.e., the vector bundle
 $\mathbb {E}=\pi _*\omega _{\overline {\mathcal {C}}_{g,n}/ \overline {\mathcal {M}}_{g,n}}$
. For all
$\mathbb {E}=\pi _*\omega _{\overline {\mathcal {C}}_{g,n}/ \overline {\mathcal {M}}_{g,n}}$
. For all
 $\alpha \in \mathbb {C}$
, we denote
$\alpha \in \mathbb {C}$
, we denote
 $\Lambda _g(\alpha )=\sum _{j=0}^g\alpha ^{g-j} \lambda _j$
, and
$\Lambda _g(\alpha )=\sum _{j=0}^g\alpha ^{g-j} \lambda _j$
, and
 $\Lambda ^\vee _g(\alpha )=(-1)^g\Lambda _g(-\alpha )$
.Footnote
1
$\Lambda ^\vee _g(\alpha )=(-1)^g\Lambda _g(-\alpha )$
.Footnote
1
-
• For all
 $1\leq i\leq n$
, we denote
$1\leq i\leq n$
, we denote
 $\psi _i$
the Chern class of the cotangent line at the ith marking
$\psi _i$
the Chern class of the cotangent line at the ith marking
 $\mathcal {L}_i=\sigma _i^*(\omega _{\overline {\mathcal {C}}_{g,n}/ \overline {\mathcal {M}}_{g,n}})$
.
$\mathcal {L}_i=\sigma _i^*(\omega _{\overline {\mathcal {C}}_{g,n}/ \overline {\mathcal {M}}_{g,n}})$
.
A Hodge integral is an intersection number of the form:
where
![]() $k_1,\ldots ,k_n$
are nonnegative integers and
$k_1,\ldots ,k_n$
are nonnegative integers and
![]() $t_1,\ldots ,t_m$
are complex numbers. If
$t_1,\ldots ,t_m$
are complex numbers. If
![]() $m=1,2,$
or 3, then the above integral is called a linear, double, or triple Hodge integrals, respectively. Relations between linear Hodge integrals where proved in [Reference Faber and PandharipandeFP00a] using the Gromov–Witten theory of
$m=1,2,$
or 3, then the above integral is called a linear, double, or triple Hodge integrals, respectively. Relations between linear Hodge integrals where proved in [Reference Faber and PandharipandeFP00a] using the Gromov–Witten theory of
![]() $\mathbb {P}^1$
and the localization formula of [Reference Graber and PandharipandeGP99]. This approach was also used in [Reference Faber and PandharipandeFP00b] and [Reference Tian and ZhouTZ03] to prove certain properties of triple Hodge integrals. Linear and triple Hodge integrals naturally appeared in the GW-theory of Calabi–Yau 3-folds, thus explaining a more abundant literature on the topic. However, double Hodge integrals have appeared recently in the quantization of Witten–Kontsevich generating series (see [Reference BlotBlo20]), in the theory of spin Hurwitz numbers (see [Reference Giacchetto, Kramer and LewańskiGKL21]), and in the GW theory of blow-ups of smooth surfaces (see [Reference Giacchetto, Kramer, Lewa’nski and SauvagetGKLS22]).
$\mathbb {P}^1$
and the localization formula of [Reference Graber and PandharipandeGP99]. This approach was also used in [Reference Faber and PandharipandeFP00b] and [Reference Tian and ZhouTZ03] to prove certain properties of triple Hodge integrals. Linear and triple Hodge integrals naturally appeared in the GW-theory of Calabi–Yau 3-folds, thus explaining a more abundant literature on the topic. However, double Hodge integrals have appeared recently in the quantization of Witten–Kontsevich generating series (see [Reference BlotBlo20]), in the theory of spin Hurwitz numbers (see [Reference Giacchetto, Kramer and LewańskiGKL21]), and in the GW theory of blow-ups of smooth surfaces (see [Reference Giacchetto, Kramer, Lewa’nski and SauvagetGKLS22]).
In the present note, we consider the following power series in
![]() $\mathbb {C}[\alpha ][\![t]\!]$
defined using double Hodge integrals:
$\mathbb {C}[\alpha ][\![t]\!]$
defined using double Hodge integrals:
 $$ \begin{align*} P_a(\alpha ,t)=\sum_{g\geq0} t^{g}\left( \int_{\overline{\mathcal{M}}_{g,n+1}}\!\!\!\!\!\!\!\!\!\!\!\! \frac{\Lambda_{g}^{\vee}(1)\Lambda_{g}^{\vee}(\alpha )}{1-\psi_0}\prod_{i=1}^{n} {(2a_i+1)!!(-4\psi_i)^{a_i}}{}\right) \text{exp}\left(\frac{t}{24}\right), \end{align*} $$
$$ \begin{align*} P_a(\alpha ,t)=\sum_{g\geq0} t^{g}\left( \int_{\overline{\mathcal{M}}_{g,n+1}}\!\!\!\!\!\!\!\!\!\!\!\! \frac{\Lambda_{g}^{\vee}(1)\Lambda_{g}^{\vee}(\alpha )}{1-\psi_0}\prod_{i=1}^{n} {(2a_i+1)!!(-4\psi_i)^{a_i}}{}\right) \text{exp}\left(\frac{t}{24}\right), \end{align*} $$
where
![]() $a=(a_1,\ldots ,a_n)$
is a vector of nonnegative integers. If
$a=(a_1,\ldots ,a_n)$
is a vector of nonnegative integers. If
![]() $n=1$
, we use the convention:
$n=1$
, we use the convention:
![]() $\int _{\overline {\mathcal {M}}_{0,2}} \psi _1^a \frac {\Lambda _{g}^{\vee }(1)\Lambda _{g}^{\vee }(\alpha ))}{1- \psi _2}=(-1)^a$
.
$\int _{\overline {\mathcal {M}}_{0,2}} \psi _1^a \frac {\Lambda _{g}^{\vee }(1)\Lambda _{g}^{\vee }(\alpha ))}{1- \psi _2}=(-1)^a$
.
Theorem 1.1
![]() $P_a(\alpha ,t)$
is a monic polynomial in
$P_a(\alpha ,t)$
is a monic polynomial in
![]() $\mathbb {C}[\alpha ][t]$
of degree
$\mathbb {C}[\alpha ][t]$
of degree
![]() $|a|$
in t.
$|a|$
in t.
Here, we provide the first values of
![]() $P_a(-\alpha -1,t)$
. In the list below, we omit the variables
$P_a(-\alpha -1,t)$
. In the list below, we omit the variables
![]() $-\alpha -1$
and t in the notation:
$-\alpha -1$
and t in the notation:
 $$ \begin{align*} &P_{()}= 1.\\[7pt] &P_{(1)}= t+12.\\[7pt] &P_{(2)}=t^2 - 10 \alpha t + 240. \\ &P_{(1,1)}=t^2 - 12 t. \\[7pt] &P_{(3)}=t^3 + (-77/3 \alpha - 28) t^2 + 280 t +6720. \\ &P_{(2,1)}= t^3 + (-10\alpha - 48)t^2 +(240\alpha + 240)t. \\ &P_{(1,1,1)}=t^3 - 72t^2+432t. \\[7pt] & P_{(4)}=t^4+ (-43\alpha - 72)t^3 + (126\alpha ^2 + 756\alpha + 840)t^2 + 10080t + 241920. \\ & P_{(3,1)}= t^4+ (-77/3 \alpha - 100) t^3+ (1232 \alpha + 1624) t^2. \\ & P_{(2,2)}=t^4+ (20\alpha + 100)t^3+(-100\alpha ^2 - 1360\alpha - 1680)t^2. \\ & P_{(2,1,1)}=t^4+ (-10\alpha - 132)t^3 + (840\alpha + 3120)t^2 +(-8640\alpha - 8640)t. \\ & P_{(1,1,1,1)}=t^4 - 168t^3 + 5616t^2 -20736t.\end{align*} $$
$$ \begin{align*} &P_{()}= 1.\\[7pt] &P_{(1)}= t+12.\\[7pt] &P_{(2)}=t^2 - 10 \alpha t + 240. \\ &P_{(1,1)}=t^2 - 12 t. \\[7pt] &P_{(3)}=t^3 + (-77/3 \alpha - 28) t^2 + 280 t +6720. \\ &P_{(2,1)}= t^3 + (-10\alpha - 48)t^2 +(240\alpha + 240)t. \\ &P_{(1,1,1)}=t^3 - 72t^2+432t. \\[7pt] & P_{(4)}=t^4+ (-43\alpha - 72)t^3 + (126\alpha ^2 + 756\alpha + 840)t^2 + 10080t + 241920. \\ & P_{(3,1)}= t^4+ (-77/3 \alpha - 100) t^3+ (1232 \alpha + 1624) t^2. \\ & P_{(2,2)}=t^4+ (20\alpha + 100)t^3+(-100\alpha ^2 - 1360\alpha - 1680)t^2. \\ & P_{(2,1,1)}=t^4+ (-10\alpha - 132)t^3 + (840\alpha + 3120)t^2 +(-8640\alpha - 8640)t. \\ & P_{(1,1,1,1)}=t^4 - 168t^3 + 5616t^2 -20736t.\end{align*} $$
Considering these first values, we conjecture that
![]() $P_a$
is a polynomial of total degree
$P_a$
is a polynomial of total degree
![]() $|a|$
in both variables t and
$|a|$
in both variables t and
![]() $\alpha $
.
$\alpha $
.
2 Preliminaries
We denote by
![]() $\overline {\mathcal {M}}_{g,n}(\mathbb {P}^1,1),$
the moduli space of stable maps of degree
$\overline {\mathcal {M}}_{g,n}(\mathbb {P}^1,1),$
the moduli space of stable maps of degree
![]() $1$
to
$1$
to
![]() $\mathbb {P}^1$
. It is a proper DM stack of virtual dimension
$\mathbb {P}^1$
. It is a proper DM stack of virtual dimension
![]() $2g+n$
. Here, we can define in an analogous way the Hodge bundle
$2g+n$
. Here, we can define in an analogous way the Hodge bundle
![]() $\mathbb {E}$
, the cotangent line bundles
$\mathbb {E}$
, the cotangent line bundles
![]() $\mathcal {L}_i$
and we denote again
$\mathcal {L}_i$
and we denote again
![]() $\lambda _i$
and
$\lambda _i$
and
![]() $\psi _i$
the respective Chern classes. We also have the forgetful and evaluation maps
$\psi _i$
the respective Chern classes. We also have the forgetful and evaluation maps
Throughout this note, the enumeration of markings starts from
![]() $0$
. Furthermore,
$0$
. Furthermore,
![]() $\pi $
is the morphism that forgets the marking
$\pi $
is the morphism that forgets the marking
![]() $p_0$
and
$p_0$
and
![]() $ev_i$
is the evaluation of a stable map to the ith marked point. The vector bundle
$ev_i$
is the evaluation of a stable map to the ith marked point. The vector bundle
![]() $T:=R^1\pi _*(ev_0^*\mathcal {O}_{\mathbb {P}^1}(-1))$
is of rank g and we denote by y its top Chern class. We will denote:
$T:=R^1\pi _*(ev_0^*\mathcal {O}_{\mathbb {P}^1}(-1))$
is of rank g and we denote by y its top Chern class. We will denote:
 $$ \begin{align*} \langle \prod_{i=0}^{n-1}\tau_{a_i}(\omega)|y\rangle_{g,1}^{\mathbb{P}^1}:= \int_{[\overline{\mathcal{M}}_{g,n}(\mathbb{P}^1,1)]^{vir}}\prod_{i=0}^{n-1}\psi_i^{a_i}ev_i^*(\omega)y, \end{align*} $$
$$ \begin{align*} \langle \prod_{i=0}^{n-1}\tau_{a_i}(\omega)|y\rangle_{g,1}^{\mathbb{P}^1}:= \int_{[\overline{\mathcal{M}}_{g,n}(\mathbb{P}^1,1)]^{vir}}\prod_{i=0}^{n-1}\psi_i^{a_i}ev_i^*(\omega)y, \end{align*} $$
where
![]() $\omega $
denotes the class of a point in
$\omega $
denotes the class of a point in
![]() $\mathbb {P}^1$
.
$\mathbb {P}^1$
.
Theorem 2.1 (Localization Formula [Reference Graber and PandharipandeGP99, Reference Faber and PandharipandeFP00a])
Let
![]() $g\in \mathbb {Z}_{\geq 0}$
, and let
$g\in \mathbb {Z}_{\geq 0}$
, and let
![]() $a\in \mathbb {Z}^n_{\geq 0}$
such that
$a\in \mathbb {Z}^n_{\geq 0}$
such that
![]() $|a|\leq g$
. Then, for all complex numbers
$|a|\leq g$
. Then, for all complex numbers
![]() ${\alpha }$
, and
${\alpha }$
, and
![]() $t\in \mathbb {C}^*$
, we have
$t\in \mathbb {C}^*$
, we have
 $$ \begin{align*} \langle \prod_{i=1}^n\tau_{a_i}(\omega)|y\rangle_{g,1}^{\mathbb{P}^1}= \sum_{g_1+g_2=g} &\int_{\overline{\mathcal{M}}_{g_1,n+1}}t^{n}\prod_{i=1}^n\psi_i^{a_i} \frac{\Lambda^{\vee}_{g_1}(t)\Lambda_{g_1}^{\vee}(\alpha t)}{t(t-\psi_0)}\ \\ &\times\int_{\overline{\mathcal{M}}_{g_2,1}} \frac{\Lambda_{g_2}^{\vee}(-t)\Lambda_{g_2}^{\vee}((\alpha +1)t)}{-t(-t-\psi_0)}. \end{align*} $$
$$ \begin{align*} \langle \prod_{i=1}^n\tau_{a_i}(\omega)|y\rangle_{g,1}^{\mathbb{P}^1}= \sum_{g_1+g_2=g} &\int_{\overline{\mathcal{M}}_{g_1,n+1}}t^{n}\prod_{i=1}^n\psi_i^{a_i} \frac{\Lambda^{\vee}_{g_1}(t)\Lambda_{g_1}^{\vee}(\alpha t)}{t(t-\psi_0)}\ \\ &\times\int_{\overline{\mathcal{M}}_{g_2,1}} \frac{\Lambda_{g_2}^{\vee}(-t)\Lambda_{g_2}^{\vee}((\alpha +1)t)}{-t(-t-\psi_0)}. \end{align*} $$
Here, we use the convention
![]() $\int _{\overline {\mathcal {M}}_{0,1}}\psi _0^a=1$
.
$\int _{\overline {\mathcal {M}}_{0,1}}\psi _0^a=1$
.
Proposition 2.2 (Proposition 4.1 of [Reference Tian and ZhouTZ03])
For all complex numbers
![]() $\alpha $
, we have
$\alpha $
, we have
 $$ \begin{align*} F(\alpha ,t)=1+\sum_{g>0}t^{2g}\int_{\overline{\mathcal{M}}_{g,1}}\frac{\Lambda_{g}^{\vee}(1)\Lambda_{g}^{\vee}(\alpha )}{1-\psi_0}=\text{exp} \left(-\frac{t^2}{24}\right). \end{align*} $$
$$ \begin{align*} F(\alpha ,t)=1+\sum_{g>0}t^{2g}\int_{\overline{\mathcal{M}}_{g,1}}\frac{\Lambda_{g}^{\vee}(1)\Lambda_{g}^{\vee}(\alpha )}{1-\psi_0}=\text{exp} \left(-\frac{t^2}{24}\right). \end{align*} $$
Besides, we have the String and Dilaton equation for Hodge integrals.
Proposition 2.3 Let
![]() $g,n\in \mathbb {Z}_{\geq 0}$
such that
$g,n\in \mathbb {Z}_{\geq 0}$
such that
![]() $2g-2+n>0$
.
$2g-2+n>0$
.
-
(i) [Dilaton equation for Hodge integrals] Let
 $(a_1,\dots ,a_{n})\in \mathbb {Z}_{\geq 0}^{n}$
and assume that there exist
$(a_1,\dots ,a_{n})\in \mathbb {Z}_{\geq 0}^{n}$
and assume that there exist
 $i_0$
such that
$i_0$
such that
 $a_{i_0}=1$
. Then
$a_{i_0}=1$
. Then  $$ \begin{align*} \int_{\overline{\mathcal{M}}_{g,n+1}}\frac{\psi_{i_0}\prod_{i\neq i_0}\psi_i^{a_i}\prod_{j=1}^g\lambda_k^{b_k}}{1-\psi_0}= (2g-2+n) \int_{\overline{\mathcal{M}}_{g,n}}\frac{\prod_{i=1}^{n-1}\psi_i^{a_i}\prod_{j=1}^g\lambda_k^{b_k}}{1-\psi_0}. \end{align*} $$
$$ \begin{align*} \int_{\overline{\mathcal{M}}_{g,n+1}}\frac{\psi_{i_0}\prod_{i\neq i_0}\psi_i^{a_i}\prod_{j=1}^g\lambda_k^{b_k}}{1-\psi_0}= (2g-2+n) \int_{\overline{\mathcal{M}}_{g,n}}\frac{\prod_{i=1}^{n-1}\psi_i^{a_i}\prod_{j=1}^g\lambda_k^{b_k}}{1-\psi_0}. \end{align*} $$
-
(ii) [String equation for Hodge integrals] Let
 $(a_1,\dots ,a_{n})\in \mathbb {Z}_{\geq 0}^{n}$
and assume that there exist
$(a_1,\dots ,a_{n})\in \mathbb {Z}_{\geq 0}^{n}$
and assume that there exist
 $i_0$
such that
$i_0$
such that
 $a_{i_0}=0$
. Then we have
$a_{i_0}=0$
. Then we have  $$ \begin{align*} \int_{\overline{\mathcal{M}}_{g,n+1}}\frac{\prod_{i=1}^n\psi_i^{a_i}\prod_{j=1}^g\lambda_k^{b_k}}{1-\psi_0}&= \int_{\overline{\mathcal{M}}_{g,n}}\frac{\prod_{i=1}^{n-1}\psi_i^{a_i}\prod_{j=1}^g\lambda_k^{b_k}}{1-\psi_0}\\&\quad + \sum_{j=1}^n\int_{\overline{\mathcal{M}}_{g,n}}\frac{\psi_j^{a_j-1}\prod_{i\neq j}\psi_i^{a_i}\prod_{k=1}^g\lambda_k^{b_k}}{1-\psi_0}. \end{align*} $$
$$ \begin{align*} \int_{\overline{\mathcal{M}}_{g,n+1}}\frac{\prod_{i=1}^n\psi_i^{a_i}\prod_{j=1}^g\lambda_k^{b_k}}{1-\psi_0}&= \int_{\overline{\mathcal{M}}_{g,n}}\frac{\prod_{i=1}^{n-1}\psi_i^{a_i}\prod_{j=1}^g\lambda_k^{b_k}}{1-\psi_0}\\&\quad + \sum_{j=1}^n\int_{\overline{\mathcal{M}}_{g,n}}\frac{\psi_j^{a_j-1}\prod_{i\neq j}\psi_i^{a_i}\prod_{k=1}^g\lambda_k^{b_k}}{1-\psi_0}. \end{align*} $$
3 The calculation
Note that the GW-invariant
![]() $\langle \prod _{i=1}^n\tau _{a_i} (\omega )|y\rangle _{g,1}^{\mathbb {P}^1}$
is 0 unless
$\langle \prod _{i=1}^n\tau _{a_i} (\omega )|y\rangle _{g,1}^{\mathbb {P}^1}$
is 0 unless
![]() $|a|=g$
for dimensional reasons. Indeed,
$|a|=g$
for dimensional reasons. Indeed,
![]() $\text {dim}_{\mathbb {C}}[\overline {\mathcal {M}}_{g,n} (\mathbb {P}^1,1)]^{\text {vir}}=2g+n$
and the cycle we are integrating is in codimension
$\text {dim}_{\mathbb {C}}[\overline {\mathcal {M}}_{g,n} (\mathbb {P}^1,1)]^{\text {vir}}=2g+n$
and the cycle we are integrating is in codimension
![]() $g+|a|+n$
. Using the above localization formula, and Lemma 2.1 of [Reference Tian and ZhouTZ03] the intersection number
$g+|a|+n$
. Using the above localization formula, and Lemma 2.1 of [Reference Tian and ZhouTZ03] the intersection number
![]() $\langle \prod _{i=1}^n\tau _{a_i}(\omega )|y\rangle _{g,1}^{\mathbb {P}^1}$
is expressed as
$\langle \prod _{i=1}^n\tau _{a_i}(\omega )|y\rangle _{g,1}^{\mathbb {P}^1}$
is expressed as
 $$ \begin{align*} &\sum_{g_1+g_2=g}\int_{\overline{\mathcal{M}}_{g_1,n+1}}\!\!\!\!\!\!t^{n}\prod_{i=1}^n\psi_i^{a_i} \frac{\Lambda_{g_1}^{\vee}(t)\Lambda_{g_1}^{\vee}(\alpha t)}{t(t-\psi_0)}\ \cdot \int_{\overline{\mathcal{M}}_{g_2,1}} \frac{\Lambda^{\vee}_{g_2}(-t)\Lambda_{g_2}^{\vee}((\alpha +1)t)}{-t(-t-\psi_0)}\\ =& \sum_{g_1+g_2=g} t^{|a|-g_1}(-t)^{-g_2}\int_{\overline{\mathcal{M}}_{g_1,n+1}} \prod_{i=1}^{n}\psi^{a_i}\frac{\Lambda_{g_1}^{\vee}(1)\Lambda_{g_1}^{\vee}(\alpha )}{1-\psi_0} \times \int_{\overline{\mathcal{M}}_{g_2,1}}\frac{\Lambda_{g_2}^{\vee}(1)\Lambda_{g_2}^{\vee}(-(\alpha +1))}{1-\psi_0} \\ =& \ t^{|a|-g}\sum_{g_1+g_2=g}\int_{\overline{\mathcal{M}}_{g_1,n+1}} \prod_{i=1}^{n}\psi^{a_i}\frac{\Lambda_{g_1}^{\vee}(1)\Lambda_{g_1}^{\vee}(\alpha )}{1-\psi_0}\cdot \int_{\overline{\mathcal{M}}_{g_2,1}}\psi_0^{3g_2-2}. \end{align*} $$
$$ \begin{align*} &\sum_{g_1+g_2=g}\int_{\overline{\mathcal{M}}_{g_1,n+1}}\!\!\!\!\!\!t^{n}\prod_{i=1}^n\psi_i^{a_i} \frac{\Lambda_{g_1}^{\vee}(t)\Lambda_{g_1}^{\vee}(\alpha t)}{t(t-\psi_0)}\ \cdot \int_{\overline{\mathcal{M}}_{g_2,1}} \frac{\Lambda^{\vee}_{g_2}(-t)\Lambda_{g_2}^{\vee}((\alpha +1)t)}{-t(-t-\psi_0)}\\ =& \sum_{g_1+g_2=g} t^{|a|-g_1}(-t)^{-g_2}\int_{\overline{\mathcal{M}}_{g_1,n+1}} \prod_{i=1}^{n}\psi^{a_i}\frac{\Lambda_{g_1}^{\vee}(1)\Lambda_{g_1}^{\vee}(\alpha )}{1-\psi_0} \times \int_{\overline{\mathcal{M}}_{g_2,1}}\frac{\Lambda_{g_2}^{\vee}(1)\Lambda_{g_2}^{\vee}(-(\alpha +1))}{1-\psi_0} \\ =& \ t^{|a|-g}\sum_{g_1+g_2=g}\int_{\overline{\mathcal{M}}_{g_1,n+1}} \prod_{i=1}^{n}\psi^{a_i}\frac{\Lambda_{g_1}^{\vee}(1)\Lambda_{g_1}^{\vee}(\alpha )}{1-\psi_0}\cdot \int_{\overline{\mathcal{M}}_{g_2,1}}\psi_0^{3g_2-2}. \end{align*} $$
In the last equation, we used Proposition 2.2 in order to replace
![]() $\int _{\overline {\mathcal {M}}_{g_2,1}}\frac {\Lambda _{g_2}^{\vee } (1)\Lambda _{g_2}^{\vee }(-(\alpha +1))}{1-\psi _0}$
with
$\int _{\overline {\mathcal {M}}_{g_2,1}}\frac {\Lambda _{g_2}^{\vee } (1)\Lambda _{g_2}^{\vee }(-(\alpha +1))}{1-\psi _0}$
with
![]() $(-1)^{g_2}\int _{\overline {\mathcal {M}}_{g_2,1}}\psi _0^{3g_2-2}$
.
$(-1)^{g_2}\int _{\overline {\mathcal {M}}_{g_2,1}}\psi _0^{3g_2-2}$
.
We define
 $$ \begin{align*} A_{g,a}(\alpha ) = \sum_{g_1+g_2=g}\int_{\overline{\mathcal{M}}_{g_1,n+1}} \prod_{i=1}^{n}\psi^{a_i}\frac{\Lambda_{g_1}^{\vee}(1)\Lambda_{g_1}^{\vee}(\alpha )}{1-\psi_0}\cdot \int_{\overline{\mathcal{M}}_{g_2,1}}\psi_0^{3g_2-2}. \end{align*} $$
$$ \begin{align*} A_{g,a}(\alpha ) = \sum_{g_1+g_2=g}\int_{\overline{\mathcal{M}}_{g_1,n+1}} \prod_{i=1}^{n}\psi^{a_i}\frac{\Lambda_{g_1}^{\vee}(1)\Lambda_{g_1}^{\vee}(\alpha )}{1-\psi_0}\cdot \int_{\overline{\mathcal{M}}_{g_2,1}}\psi_0^{3g_2-2}. \end{align*} $$
Then, we have
 $$ \begin{align*} A_{g,a}(\alpha )= \left\{\begin{matrix} 0, &|a|<g, \\ \langle \prod_{i=1}^n\tau_{a_i}(\omega)|y\rangle_{g,1}^{\mathbb{P}^1}, & |a|=g. \end{matrix} \right. \end{align*} $$
$$ \begin{align*} A_{g,a}(\alpha )= \left\{\begin{matrix} 0, &|a|<g, \\ \langle \prod_{i=1}^n\tau_{a_i}(\omega)|y\rangle_{g,1}^{\mathbb{P}^1}, & |a|=g. \end{matrix} \right. \end{align*} $$
By the definition of
![]() $\Lambda _g^{\vee }(t),$
we see that
$\Lambda _g^{\vee }(t),$
we see that
![]() $\Lambda _g^{\vee }(1)\Lambda _g^{\vee }(-(\alpha +1))$
is a polynomial in
$\Lambda _g^{\vee }(1)\Lambda _g^{\vee }(-(\alpha +1))$
is a polynomial in
![]() $\alpha $
of degree g, which actually determines the degree of
$\alpha $
of degree g, which actually determines the degree of
![]() $A_g(\alpha )$
.
$A_g(\alpha )$
.
We now present a proof for the main result.
Proof (of Theorem 1.1)
We begin by stating the well-known fact
 $$ \begin{align*} 1 + \sum_{g>0}t^{g}\int_{\overline{\mathcal{M}}_{g,1}}\psi_0^{3g-2} =\exp\left({\frac{t}{24}}\right) \end{align*} $$
$$ \begin{align*} 1 + \sum_{g>0}t^{g}\int_{\overline{\mathcal{M}}_{g,1}}\psi_0^{3g-2} =\exp\left({\frac{t}{24}}\right) \end{align*} $$
proven in Section 3.1 of [Reference Faber and PandharipandeFP00a]. Now, we consider the product of
![]() $\exp \left ({\frac {t}{24}}\right )$
and
$\exp \left ({\frac {t}{24}}\right )$
and
 $$ \begin{align*} \sum_{g\geq0} t^{g}\left( \int_{\overline{\mathcal{M}}_{g,n+1}}\!\!\!\!\!\!\!\!\!\!\!\! \frac{\Lambda_{g}^{\vee}(1)\Lambda_{g}^{\vee}(\alpha )}{1-\psi_0}\prod_{i=1}^{n} {(2a_i+1)!!(-4\psi_i)^{a_i}}{}\right) \end{align*} $$
$$ \begin{align*} \sum_{g\geq0} t^{g}\left( \int_{\overline{\mathcal{M}}_{g,n+1}}\!\!\!\!\!\!\!\!\!\!\!\! \frac{\Lambda_{g}^{\vee}(1)\Lambda_{g}^{\vee}(\alpha )}{1-\psi_0}\prod_{i=1}^{n} {(2a_i+1)!!(-4\psi_i)^{a_i}}{}\right) \end{align*} $$
to obtain a new power series whose coefficients in degree g are given by
 $$ \begin{align*} \sum_{g_1+g_2=g}\int_{\overline{\mathcal{M}}_{g_1,n+1}}\prod_{i=1}^{n}(2a_i+1)!!(-4)^{a_i} \prod_{i=1}^{n}\psi^{a_i}\frac{\Lambda_{g_1}^{\vee}(1)\Lambda_{g_1}^{\vee}(\alpha )}{1-\psi_0}\cdot \int_{\overline{\mathcal{M}}_{g_2,1}}\psi_0^{3g_2-2}. \end{align*} $$
$$ \begin{align*} \sum_{g_1+g_2=g}\int_{\overline{\mathcal{M}}_{g_1,n+1}}\prod_{i=1}^{n}(2a_i+1)!!(-4)^{a_i} \prod_{i=1}^{n}\psi^{a_i}\frac{\Lambda_{g_1}^{\vee}(1)\Lambda_{g_1}^{\vee}(\alpha )}{1-\psi_0}\cdot \int_{\overline{\mathcal{M}}_{g_2,1}}\psi_0^{3g_2-2}. \end{align*} $$
This is exactly
![]() $A_{g,a}(\alpha )\cdot \prod _{i=1}^{n}(2a_i+1)!!(-4)^{a_i}$
. Hence, we can rewrite the power series
$A_{g,a}(\alpha )\cdot \prod _{i=1}^{n}(2a_i+1)!!(-4)^{a_i}$
. Hence, we can rewrite the power series
![]() $P_a(\alpha ,t)$
in the form
$P_a(\alpha ,t)$
in the form
 $$ \begin{align*} P_a(\alpha ,t)=\prod_{i=1}^{n}(2a_i+1)!!(-4)^{a_i}\sum_{g\geq0}t^{g}A_{g,a}(\alpha ). \end{align*} $$
$$ \begin{align*} P_a(\alpha ,t)=\prod_{i=1}^{n}(2a_i+1)!!(-4)^{a_i}\sum_{g\geq0}t^{g}A_{g,a}(\alpha ). \end{align*} $$
As it is computed in the start of Section 3, we have that the numbers
![]() $A_{g,a}(\alpha )$
vanish when
$A_{g,a}(\alpha )$
vanish when
![]() $g>|a|$
. Hence, we get that all coefficients of the power series
$g>|a|$
. Hence, we get that all coefficients of the power series
![]() $P_a(\alpha ,t)$
vanish when
$P_a(\alpha ,t)$
vanish when
![]() $g> |a|$
, i.e.
$g> |a|$
, i.e.
![]() $P_a(\alpha ,t)$
is a polynomial of degree
$P_a(\alpha ,t)$
is a polynomial of degree
![]() $|a|$
. Furthermore, the top coefficient of
$|a|$
. Furthermore, the top coefficient of
![]() $P_a(\alpha ,t)$
, i.e., the coefficient of
$P_a(\alpha ,t)$
, i.e., the coefficient of
![]() $t^{|a|}$
is given by
$t^{|a|}$
is given by
 $$ \begin{align*} \langle \prod_{i=1}^n (-4)^{a_i}(2a_i+1)!! \tau_{a_i}(\omega)|y\rangle_{|a|,1}^{\mathbb{P}^1}. \end{align*} $$
$$ \begin{align*} \langle \prod_{i=1}^n (-4)^{a_i}(2a_i+1)!! \tau_{a_i}(\omega)|y\rangle_{|a|,1}^{\mathbb{P}^1}. \end{align*} $$
This value is computed in [Reference Kiem and LiKL11] and is actually equal to
![]() $1$
. In particular, the number
$1$
. In particular, the number
![]() $\prod _{i=1}^n (-4)^{a_i}(2a_i+1)!! $
is here to make the polynomial monic.
$\prod _{i=1}^n (-4)^{a_i}(2a_i+1)!! $
is here to make the polynomial monic.
We now prove several other properties of the polynomials
![]() $P_a$
.
$P_a$
.
Proposition 3.1 The constant term
![]() $c_0$
of
$c_0$
of
![]() $P_a(\alpha ,t)$
is nonzero if and only if
$P_a(\alpha ,t)$
is nonzero if and only if
![]() $n=1,$
where then
$n=1,$
where then
![]() $c_0=(-1)^a\prod _{i=1}^n (-4)^{a_i}(2a_i+1)!!$
or if
$c_0=(-1)^a\prod _{i=1}^n (-4)^{a_i}(2a_i+1)!!$
or if
![]() $n>1$
and
$n>1$
and
![]() $\sum _{i=1}^na_i\leq n-2$
where then
$\sum _{i=1}^na_i\leq n-2$
where then
 $$ \begin{align*} c_0=\prod_{i=1}^n (-4)^{a_i}(2a_i+1)!!\frac{(n-2)!}{a_1!\dots (n-2-\sum{a_i})!}. \end{align*} $$
$$ \begin{align*} c_0=\prod_{i=1}^n (-4)^{a_i}(2a_i+1)!!\frac{(n-2)!}{a_1!\dots (n-2-\sum{a_i})!}. \end{align*} $$
Proof We only compute the integrals appearing in the constant term of this polynomial since then we only have to multiply with
![]() $\prod _{i=1}^{n}(2a_i+1)!!(-4)^{a_i}$
. The integral in the constant term of
$\prod _{i=1}^{n}(2a_i+1)!!(-4)^{a_i}$
. The integral in the constant term of
![]() $P_a(\alpha ,t)$
is given by
$P_a(\alpha ,t)$
is given by
![]() $\int _{\overline {\mathcal {M}}_{0,n+1}}\frac {\prod _{i=1}^n\psi _i^{a_i}}{1-\psi _0}$
. When
$\int _{\overline {\mathcal {M}}_{0,n+1}}\frac {\prod _{i=1}^n\psi _i^{a_i}}{1-\psi _0}$
. When
![]() $n=1$
, using the convention
$n=1$
, using the convention
![]() $\int _{\overline {\mathcal {M}}_{0,2}}\frac {\psi _1^{a}}{1-\psi _0}=(-1)^a$
, we get that
$\int _{\overline {\mathcal {M}}_{0,2}}\frac {\psi _1^{a}}{1-\psi _0}=(-1)^a$
, we get that
 $$ \begin{align*} c_0=(-1)^a\prod_{i=1}^n (-4)^{a_i}(2a_i+1)!!. \end{align*} $$
$$ \begin{align*} c_0=(-1)^a\prod_{i=1}^n (-4)^{a_i}(2a_i+1)!!. \end{align*} $$
When
![]() $n>1$
, if
$n>1$
, if
![]() $\sum _{i=1}^na_i>n-2$
, then
$\sum _{i=1}^na_i>n-2$
, then
![]() $c_0$
is zero for dimensional reasons. Otherwise, we have
$c_0$
is zero for dimensional reasons. Otherwise, we have
 $$ \begin{align*} \hspace{-15pt}\int_{\overline{\mathcal{M}}_{0,n+1}}\frac{\prod_{i=1}^n\psi_i^{a_i}}{1-\psi_0}=\int_{\overline{\mathcal{M}}_{0,n+1}} \psi_0^{n-2-\sum a_i}\prod_{i=1}^n\psi_i^{a_i}= \frac{(n-2)!}{a_1!\dots (n-2-\sum{a_i})!}.\\[-42pt] \end{align*} $$
$$ \begin{align*} \hspace{-15pt}\int_{\overline{\mathcal{M}}_{0,n+1}}\frac{\prod_{i=1}^n\psi_i^{a_i}}{1-\psi_0}=\int_{\overline{\mathcal{M}}_{0,n+1}} \psi_0^{n-2-\sum a_i}\prod_{i=1}^n\psi_i^{a_i}= \frac{(n-2)!}{a_1!\dots (n-2-\sum{a_i})!}.\\[-42pt] \end{align*} $$
Proposition 3.2 Let
![]() $n\geq 3$
. Then we have the following rules:
$n\geq 3$
. Then we have the following rules:
-
(i) [String equation]
 $$ \begin{align*} P_{(a_1,\dots,a_{n-1},0)}(\alpha ,t)= P_{(a_1,\dots,a_{n-1})}(\alpha ,t)- \sum_{i=1}^n (8a_i+4) P_{(a_1,..,a_i-1,\dots,a_{n-1})}(\alpha ,t). \end{align*} $$
$$ \begin{align*} P_{(a_1,\dots,a_{n-1},0)}(\alpha ,t)= P_{(a_1,\dots,a_{n-1})}(\alpha ,t)- \sum_{i=1}^n (8a_i+4) P_{(a_1,..,a_i-1,\dots,a_{n-1})}(\alpha ,t). \end{align*} $$
-
(ii) [Dilaton equation]
 $$ \begin{align*} P_{(a_1,\dots,a_{n-1},1)}(\alpha ,t)=(t-12n+24) P_{(a_1,\dots,a_{n-1})}(\alpha ,t) - 24 t P^{\prime}_{(a_1,\dots,a_{n-1})}(\alpha ,t)). \end{align*} $$
$$ \begin{align*} P_{(a_1,\dots,a_{n-1},1)}(\alpha ,t)=(t-12n+24) P_{(a_1,\dots,a_{n-1})}(\alpha ,t) - 24 t P^{\prime}_{(a_1,\dots,a_{n-1})}(\alpha ,t)). \end{align*} $$
Proof We define the power series
 $$ \begin{align*} \widetilde{P}_a(\alpha ,t)= \sum_{g\geq0} t^{g}\left(\int_{\overline{\mathcal{M}}_{g,n+1}}\prod_{i=1}^{n}\psi^{a_i} \frac{\Lambda_{g}^{\vee}(1)\Lambda_{g}^{\vee}(\alpha )}{1-\psi_0}\right). \end{align*} $$
$$ \begin{align*} \widetilde{P}_a(\alpha ,t)= \sum_{g\geq0} t^{g}\left(\int_{\overline{\mathcal{M}}_{g,n+1}}\prod_{i=1}^{n}\psi^{a_i} \frac{\Lambda_{g}^{\vee}(1)\Lambda_{g}^{\vee}(\alpha )}{1-\psi_0}\right). \end{align*} $$
Note that the following equation holds:
 $$ \begin{align*} P_a(\alpha ,t)=\prod_{i=1}^{n}(2a_i+1)!!(-4)^{a_i}\widetilde{P}_a(\alpha ,t)\exp\left(\frac{t}{24}\right). \end{align*} $$
$$ \begin{align*} P_a(\alpha ,t)=\prod_{i=1}^{n}(2a_i+1)!!(-4)^{a_i}\widetilde{P}_a(\alpha ,t)\exp\left(\frac{t}{24}\right). \end{align*} $$
We can rewrite the coefficients of
![]() $\widetilde {P}_a(\alpha ,t)$
as
$\widetilde {P}_a(\alpha ,t)$
as
 $$ \begin{align*} \sum_{k=0}^g\sum_{j=0}^g(-1)^{g+k}(a+1)^{g-j}\int_{\overline{\mathcal{M}}_{g,n+1}} \frac{\prod_{i=1}^n\psi_i^{a_i}\lambda_k\lambda_j}{1-\psi_0}. \end{align*} $$
$$ \begin{align*} \sum_{k=0}^g\sum_{j=0}^g(-1)^{g+k}(a+1)^{g-j}\int_{\overline{\mathcal{M}}_{g,n+1}} \frac{\prod_{i=1}^n\psi_i^{a_i}\lambda_k\lambda_j}{1-\psi_0}. \end{align*} $$
-
(i) Applying the String equation for Hodge integrals, we obtain the following formula:
 $$ \begin{align*} \widetilde{P}_{(a_1,\dots,a_{n-1},0)}(\alpha ,t)=\widetilde{P}_{(a_1,\dots,a_{n-1})}(\alpha ,t)+ \sum_{i=1}^n\widetilde{P}_{(a_1,..,a_i-1,\dots,a_{n-1})}(\alpha ,t). \end{align*} $$
$$ \begin{align*} \widetilde{P}_{(a_1,\dots,a_{n-1},0)}(\alpha ,t)=\widetilde{P}_{(a_1,\dots,a_{n-1})}(\alpha ,t)+ \sum_{i=1}^n\widetilde{P}_{(a_1,..,a_i-1,\dots,a_{n-1})}(\alpha ,t). \end{align*} $$
Hence, multiplying with
 $\prod _{i=1}^{n-1}(2a_i+1)!!(-4)^{a_i} \text {exp}\left (\frac {t}{24}\right )$
, we obtain the desired result after a straightforward calculation.
$\prod _{i=1}^{n-1}(2a_i+1)!!(-4)^{a_i} \text {exp}\left (\frac {t}{24}\right )$
, we obtain the desired result after a straightforward calculation. -
(ii) Applying Dilaton equation for Hodge integrals, we obtain the following formula:
 $$ \begin{align*} \widetilde{P}_{(a_1,\dots,a_{n-1},1)}(\alpha ,t)&= 2\sum_{g\geq0}gt^g\int_{\overline{\mathcal{M}}_{g,n-1}}\prod_{i=1}^{n-1}\psi_i^{a_i}\frac{\Lambda^{\vee}_g(1)\Lambda^{\vee}_g(\alpha )}{1-\psi_0} \\ &+ (n-2)\widetilde{P}_{(a_1,\dots,a_{n-1})}(\alpha ,t). \end{align*} $$
$$ \begin{align*} \widetilde{P}_{(a_1,\dots,a_{n-1},1)}(\alpha ,t)&= 2\sum_{g\geq0}gt^g\int_{\overline{\mathcal{M}}_{g,n-1}}\prod_{i=1}^{n-1}\psi_i^{a_i}\frac{\Lambda^{\vee}_g(1)\Lambda^{\vee}_g(\alpha )}{1-\psi_0} \\ &+ (n-2)\widetilde{P}_{(a_1,\dots,a_{n-1})}(\alpha ,t). \end{align*} $$
Note that the first term of the sum is equal to
 $2t\widetilde {P}^{\prime }_{(a_1,\dots ,a_{n-1})}(\alpha ,t)$
. Now, multiplying both sides of the equation above with
$2t\widetilde {P}^{\prime }_{(a_1,\dots ,a_{n-1})}(\alpha ,t)$
. Now, multiplying both sides of the equation above with  $$ \begin{align*} \prod_{i=1}^{n-1}(2a_i+1)(-4)^{a_i}\text{exp}\left(\frac{t}{24}\right), \end{align*} $$
$$ \begin{align*} \prod_{i=1}^{n-1}(2a_i+1)(-4)^{a_i}\text{exp}\left(\frac{t}{24}\right), \end{align*} $$
we have
 $$ \begin{align*} \frac{-1}{12}P_{(a_1,\dots,a_{n-1},1)}(\alpha ,t)&=(n-2)P_{(a_1,\dots,a_{n-1})}(\alpha ,t)\\ & + 2t \left(\prod_{i=1}^{n-1} (-4)^{a_i}(2a_i+1)!!\right) \widetilde{P}^{\prime}_{(a_1,\dots,a_{n-1})}(\alpha ,t)\mathrm{e}^{{t}/{24}}\\ \!\! &= (n-2)P_{(a_1,\dots,a_{n-1})}(\alpha ,t)\\ & + 2t( P^{\prime}_{(a_1,\dots,a_{n-1})}(\alpha ,t)-\frac{1}{24} P_{(a_1,\dots,a_{n-1})}(\alpha ,t)). \end{align*} $$
$$ \begin{align*} \frac{-1}{12}P_{(a_1,\dots,a_{n-1},1)}(\alpha ,t)&=(n-2)P_{(a_1,\dots,a_{n-1})}(\alpha ,t)\\ & + 2t \left(\prod_{i=1}^{n-1} (-4)^{a_i}(2a_i+1)!!\right) \widetilde{P}^{\prime}_{(a_1,\dots,a_{n-1})}(\alpha ,t)\mathrm{e}^{{t}/{24}}\\ \!\! &= (n-2)P_{(a_1,\dots,a_{n-1})}(\alpha ,t)\\ & + 2t( P^{\prime}_{(a_1,\dots,a_{n-1})}(\alpha ,t)-\frac{1}{24} P_{(a_1,\dots,a_{n-1})}(\alpha ,t)). \end{align*} $$
Finally, clearing the denominators, we obtain the desired result.
We recall Mumford’s relation
![]() $\Lambda ^\vee _g(1)\cdot \Lambda ^\vee _g(-1)=1$
(see [Reference MumfordMum83]). In particular,
$\Lambda ^\vee _g(1)\cdot \Lambda ^\vee _g(-1)=1$
(see [Reference MumfordMum83]). In particular,
![]() $P_a(-1,t)$
is defined by integrals of
$P_a(-1,t)$
is defined by integrals of
![]() $\psi $
-classes.
$\psi $
-classes.
Corollary 3.3 For any vector
![]() $a\in \mathbb {Z}^n_{\geq 0}$
, the power series
$a\in \mathbb {Z}^n_{\geq 0}$
, the power series
 $$ \begin{align*} P_a(-1,t)=\prod_{i=1}^{n}(2a_i+1)!!(-4)^{a_i}\text{exp}\left(\frac{t}{24}\right) \cdot\sum_{g\geq0}(-t)^g\int_{\overline{\mathcal{M}}_{g,n+1}} \frac{\prod_{i=1}^n\psi_i^{a_i}}{1-\psi_0} \end{align*} $$
$$ \begin{align*} P_a(-1,t)=\prod_{i=1}^{n}(2a_i+1)!!(-4)^{a_i}\text{exp}\left(\frac{t}{24}\right) \cdot\sum_{g\geq0}(-t)^g\int_{\overline{\mathcal{M}}_{g,n+1}} \frac{\prod_{i=1}^n\psi_i^{a_i}}{1-\psi_0} \end{align*} $$
is a polynomial of degree
![]() $|a|$
.
$|a|$
.
In this case, the polynomiality as well as a closed expression were proved in [Reference Liu and XuLX11].
Acknowledgments
I am very grateful to my PhD advisor Adrien Sauvaget for introducing me to this problem and for his guidance and comments throughout the whole writing of this article.