We study finite and infinite entangled graphsin the bond percolation process in three dimensionswith density $p$.After a discussion of the relevant definitions,the entanglement critical probabilities are defined.The size of the maximal entangled graph at the origin is studied for small $p$, and it is shown that this graph has radius whose tail decays at least as fast as $\exp(-\alpha n/\log n)$; indeed, the logarithm may be replaced by any iterate of logarithmfor an appropriate positive constant $\alpha$. We explore the question of almost sure uniqueness of the infinite maximal open entangled graph when $p$ is large, and we establish two relevant theorems. We make several conjectures concerning the properties of entangled graphs in percolation. http://www.statslab.cam.ac.uk/$\sim$grg/ 1991 Mathematics Subject Classification: primary 60K35; secondary 05C10, 57M25, 82B41, 82B43, 82D60.
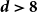 $\boldsymbol{d}\boldsymbol\gt \textbf{8}$
$\boldsymbol{d}\boldsymbol\gt \textbf{8}$