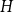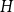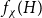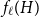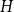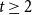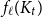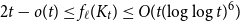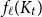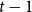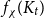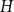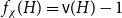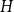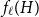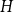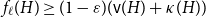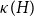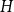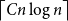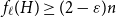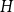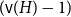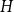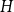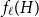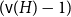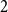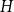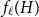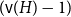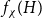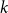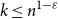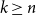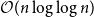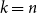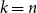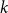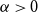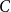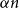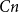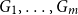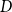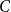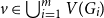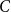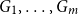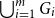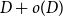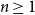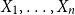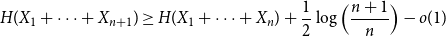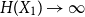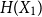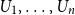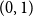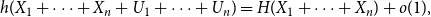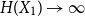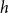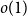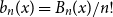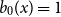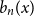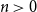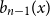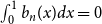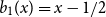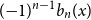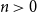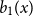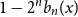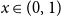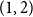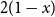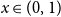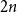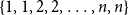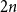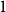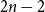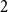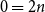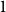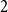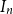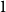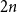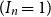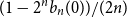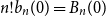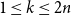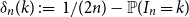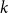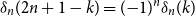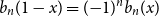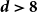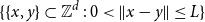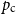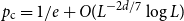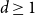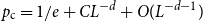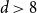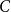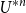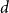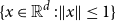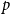Given a graph $H$, let us denote by $f_\chi (H)$ and $f_\ell (H)$, respectively, the maximum chromatic number and the maximum list chromatic number of $H$-minor-free graphs. Hadwiger’s famous colouring conjecture from 1943 states that $f_\chi (K_t)=t-1$ for every $t \ge 2$. A closely related problem that has received significant attention in the past concerns $f_\ell (K_t)$, for which it is known that $2t-o(t) \le f_\ell (K_t) \le O(t (\!\log \log t)^6)$. Thus, $f_\ell (K_t)$ is bounded away from the conjectured value $t-1$ for $f_\chi (K_t)$ by at least a constant factor. The so-called $H$-Hadwiger’s conjecture, proposed by Seymour, asks to prove that $f_\chi (H)={\textrm{v}}(H)-1$ for a given graph $H$ (which would be implied by Hadwiger’s conjecture).

In this paper, we prove several new lower bounds on $f_\ell (H)$, thus exploring the limits of a list colouring extension of $H$-Hadwiger’s conjecture. Our main results are:

• For every $\varepsilon \gt 0$ and all sufficiently large graphs $H$ we have $f_\ell (H)\ge (1-\varepsilon )({\textrm{v}}(H)+\kappa (H))$, where $\kappa (H)$ denotes the vertex-connectivity of $H$.

• For every $\varepsilon \gt 0$ there exists $C=C(\varepsilon )\gt 0$ such that asymptotically almost every $n$-vertex graph $H$ with $\left \lceil C n\log n\right \rceil$ edges satisfies $f_\ell (H)\ge (2-\varepsilon )n$.

The first result generalizes recent results on complete and complete bipartite graphs and shows that the list chromatic number of $H$-minor-free graphs is separated from the desired value of $({\textrm{v}}(H)-1)$ by a constant factor for all large graphs $H$ of linear connectivity. The second result tells us that for almost all graphs $H$ with superlogarithmic average degree $f_\ell (H)$ is separated from $({\textrm{v}}(H)-1)$ by a constant factor arbitrarily close to $2$. Conceptually these results indicate that the graphs $H$ for which $f_\ell (H)$ is close to the conjectured value $({\textrm{v}}(H)-1)$ for $f_\chi (H)$ are typically rather sparse.

Since the 1960s Mastermind has been studied for the combinatorial and information-theoretical interest the game has to offer. Many results have been discovered starting with Erdős and Rényi determining the optimal number of queries needed for two colours. For $k$ colours and $n$ positions, Chvátal found asymptotically optimal bounds when $k \le n^{1-\varepsilon }$. Following a sequence of gradual improvements for $k\geq n$ colours, the central open question is to resolve the gap between $\Omega (n)$ and $\mathcal{O}(n\log \log n)$ for $k=n$. In this paper, we resolve this gap by presenting the first algorithm for solving $k=n$ Mastermind with a linear number of queries. As a consequence, we are able to determine the query complexity of Mastermind for any parameters $k$ and $n$.

In 2003, Bohman, Frieze, and Martin initiated the study of randomly perturbed graphs and digraphs. For digraphs, they showed that for every $\alpha \gt 0$, there exists a constant $C$ such that for every $n$-vertex digraph of minimum semi-degree at least $\alpha n$, if one adds $Cn$ random edges then asymptotically almost surely the resulting digraph contains a consistently oriented Hamilton cycle. We generalize their result, showing that the hypothesis of this theorem actually asymptotically almost surely ensures the existence of every orientation of a cycle of every possible length, simultaneously. Moreover, we prove that we can relax the minimum semi-degree condition to a minimum total degree condition when considering orientations of a cycle that do not contain a large number of vertices of indegree $1$. Our proofs make use of a variant of an absorbing method of Montgomery.

A collection of graphs is nearly disjoint if every pair of them intersects in at most one vertex. We prove that if $G_1, \dots, G_m$ are nearly disjoint graphs of maximum degree at most $D$, then the following holds. For every fixed $C$, if each vertex $v \in \bigcup _{i=1}^m V(G_i)$ is contained in at most $C$ of the graphs $G_1, \dots, G_m$, then the (list) chromatic number of $\bigcup _{i=1}^m G_i$ is at most $D + o(D)$. This result confirms a special case of a conjecture of Vu and generalizes Kahn’s bound on the list chromatic index of linear uniform hypergraphs of bounded maximum degree. In fact, this result holds for the correspondence (or DP) chromatic number and thus implies a recent result of Molloy and Postle, and we derive this result from a more general list colouring result in the setting of ‘colour degrees’ that also implies a result of Reed and Sudakov.

It is proven that a conjecture of Tao (2010) holds true for log-concave random variables on the integers: For every $n \geq 1$, if $X_1,\ldots,X_n$ are i.i.d. integer-valued, log-concave random variables, then

\begin{equation*} H(X_1+\cdots +X_{n+1}) \geq H(X_1+\cdots +X_{n}) + \frac {1}{2}\log {\Bigl (\frac {n+1}{n}\Bigr )} - o(1) \end{equation*}

$H(X_1) \to \infty$

$H(X_1)$

$U_1,\ldots,U_n$

$(0,1)$

\begin{equation*} h(X_1+\cdots +X_n + U_1+\cdots +U_n) = H(X_1+\cdots +X_n) + o(1), \end{equation*}

$H(X_1) \to \infty$

$h$

$o(1)$

The factorially normalized Bernoulli polynomials 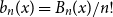$b_n(x) = B_n(x)/n!$ are known to be characterized by 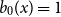$b_0(x) = 1$ and 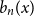$b_n(x)$ for 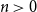$n \gt 0$ is the anti-derivative of 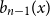$b_{n-1}(x)$ subject to 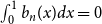$\int _0^1 b_n(x) dx = 0$. We offer a related characterization: 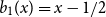$b_1(x) = x - 1/2$ and 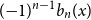$({-}1)^{n-1} b_n(x)$ for 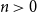$n \gt 0$ is the $n$-fold circular convolution of 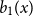$b_1(x)$ with itself. Equivalently, 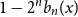$1 - 2^n b_n(x)$ is the probability density at 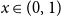$x \in (0,1)$ of the fractional part of a sum of $n$ independent random variables, each with the beta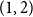$(1,2)$ probability density 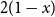$2(1-x)$ at 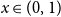$x \in (0,1)$. This result has a novel combinatorial analog, the Bernoulli clock: mark the hours of a 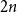$2 n$ hour clock by a uniformly random permutation of the multiset 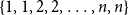$\{1,1, 2,2, \ldots, n,n\}$, meaning pick two different hours uniformly at random from the 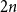$2 n$ hours and mark them 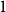$1$, then pick two different hours uniformly at random from the remaining 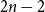$2 n - 2$ hours and mark them 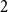$2$, and so on. Starting from hour 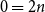$0 = 2n$, move clockwise to the first hour marked 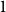$1$, continue clockwise to the first hour marked 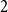$2$, and so on, continuing clockwise around the Bernoulli clock until the first of the two hours marked $n$ is encountered, at a random hour 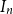$I_n$ between 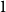$1$ and 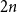$2n$. We show that for each positive integer $n$, the event 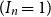$( I_n = 1)$ has probability 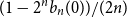$(1 - 2^n b_n(0))/(2n)$, where 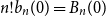$n! b_n(0) = B_n(0)$ is the $n$th Bernoulli number. For 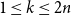$ 1 \le k \le 2 n$, the difference 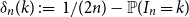$\delta _n(k)\,:\!=\, 1/(2n) -{\mathbb{P}}( I_n = k)$ is a polynomial function of 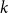$k$ with the surprising symmetry 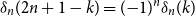$\delta _n( 2 n + 1 - k) = ({-}1)^n \delta _n(k)$, which is a combinatorial analog of the well-known symmetry of Bernoulli polynomials 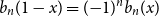$b_n(1-x) = ({-}1)^n b_n(x)$.

A spread-out lattice animal is a finite connected set of edges in $\{\{x,y\}\subset \mathbb{Z}^d\;:\;0\lt \|x-y\|\le L\}$. A lattice tree is a lattice animal with no loops. The best estimate on the critical point $p_{\textrm{c}}$ so far was achieved by Penrose (J. Stat. Phys. 77, 3–15, 1994) : $p_{\textrm{c}}=1/e+O(L^{-2d/7}\log L)$ for both models for all $d\ge 1$. In this paper, we show that $p_{\textrm{c}}=1/e+CL^{-d}+O(L^{-d-1})$ for all $d\gt 8$, where the model-dependent constant $C$ has the random-walk representation

\begin{align*} C_{\textrm{LT}}=\sum _{n=2}^\infty \frac{n+1}{2e}U^{*n}(o),&& C_{\textrm{LA}}=C_{\textrm{LT}}-\frac 1{2e^2}\sum _{n=3}^\infty U^{*n}(o), \end{align*}

$U^{*n}$

$n$

$d$

$\{x\in{\mathbb R}^d\;: \|x\|\le 1\}$

$p$