1 results
On the relationship between depth and cohomological dimension
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 876-888
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
-
Let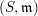
$(S,\mathfrak{m})$ be an 
$n$-dimensional regular local ring essentially of finite type over a field and let 
$\mathfrak{a}$ be an ideal of 
$S$. We prove that if 
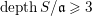$\text{depth}\,S/\mathfrak{a}\geqslant 3$, then the cohomological dimension 
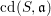$\text{cd}(S,\mathfrak{a})$ of 
$\mathfrak{a}$ is less than or equal to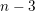 
$n-3$. This settles a conjecture of Varbaro for such an 
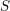$S$. We also show, under the assumption that 
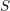$S$ has an algebraically closed residue field of characteristic zero, that if 
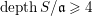$\text{depth}\,S/\mathfrak{a}\geqslant 4$, then 
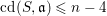$\text{cd}(S,\mathfrak{a})\leqslant n-4$ if and only if the local Picard group of the completion 
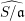$\widehat{S/\mathfrak{a}}$ is torsion. We give a number of applications, including a vanishing result on Lyubeznik’s numbers, and sharp bounds on the cohomological dimension of ideals whose quotients satisfy good depth conditions such as Serre’s conditions 
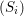$(S_{i})$.
