Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T20:17:50.750Z Has data issue: false hasContentIssue false
  • English
  • Français

On the relationship between depth and cohomological dimension

Part of: Commutative algebra: Homological methods Local theory Analytic spaces

Published online by Cambridge University Press:  03 November 2015

Hailong Dao  and
Shunsuke Takagi
Hailong Dao
Affiliation:
Department of Mathematics, University of Kansas, Lawrence, KS 66045-7523, USA email hdao@ku.edu
Shunsuke Takagi
Affiliation:
Graduate School of Mathematical Sciences, University of Tokyo, 3-8-1 Komaba, Meguro-ku, Tokyo 153-8914, Japan email stakagi@ms.u-tokyo.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 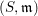$(S,\mathfrak{m})$ be an $n$-dimensional regular local ring essentially of finite type over a field and let $\mathfrak{a}$ be an ideal of 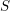$S$. We prove that if 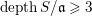$\text{depth}\,S/\mathfrak{a}\geqslant 3$, then the cohomological dimension 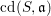$\text{cd}(S,\mathfrak{a})$ of $\mathfrak{a}$ is less than or equal to 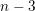$n-3$. This settles a conjecture of Varbaro for such an 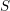$S$. We also show, under the assumption that 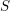$S$ has an algebraically closed residue field of characteristic zero, that if 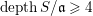$\text{depth}\,S/\mathfrak{a}\geqslant 4$, then 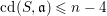$\text{cd}(S,\mathfrak{a})\leqslant n-4$ if and only if the local Picard group of the completion 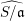$\widehat{S/\mathfrak{a}}$ is torsion. We give a number of applications, including a vanishing result on Lyubeznik’s numbers, and sharp bounds on the cohomological dimension of ideals whose quotients satisfy good depth conditions such as Serre’s conditions 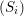$(S_{i})$.

Keywords

local cohomologycohomological dimensionlocal Picard groups

MSC classification

Primary: 13D45: Local cohomology 14B15: Local cohomology 32C36: Local cohomology of analytic spaces
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 4 , April 2016 , pp. 876 - 888
Copyright
© The Authors 2015 

References

Artin, M., Algebraic approximation of structures over complete local rings, Publ. Math. Inst. Hautes Études Sci. 36 (1969), 23–58.Google Scholar
Bănică, C. and Stănăşilă, O., Algebraic methods in the global theory of complex spaces (Editura Academiei, Bucharest and John Wiley & Sons, London–New York–Sydney, 1976).Google Scholar
Boutot, J.-F., Schéma de Picard local, Lecture Notes in Mathematics, vol. 632 (Springer, Berlin, 1978).Google Scholar
Bruns, W. and Vetter, U., Determinantal rings, Lecture Notes in Mathematics, vol. 1327 (Springer, Berlin, 1988).Google Scholar
Dao, H., Huneke, C. and Schweig, J., Bounds on the regularity and projective dimension of ideals associated to graphs, J. Algebraic Combin. 38(1) (2013), 37–55.Google Scholar
Dimca, A., Singularities and topology of hypersurfaces, Universitext (Springer, New York, 1992).CrossRefGoogle Scholar
Dutta, S. P., A theorem on smoothness–Bass-Quillen, Chow groups and intersection multiplicity of Serre, Trans. Amer. Math. Soc. 352 (2000), 1635–1645.Google Scholar
Fossum, R. M., The divisor class group of a Krull domain, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 74 (Springer, 1973).Google Scholar
Goto, S. and Watanabe, K., On graded rings I, J. Math. Soc. Japan 30 (1978), 179–213.Google Scholar
Hartshorne, R., Cohomological dimension of algebraic varieties, Ann. of Math. (2) 88 (1968), 403–450.CrossRefGoogle Scholar
Hartshorne, R., On the de Rham cohomology of algebraic varieties, Publ. Math. Inst. Hautes Études Sci. 45 (1975), 5–99.Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, Heidelberg, Berlin, 1977).Google Scholar
Hartshorne, R., Generalized divisors on Gorenstein schemes, K-Theory 8 (1994), 287–339.Google Scholar
Huneke, C., Problems in local cohomology, in Free resolutions in commutative algebra and algebraic geometry (Sundance 90), Research Notes in Mathematics, vol. 2 (Jones and Barlett, Burlington, MA, 1992), 93–108.Google Scholar
Huneke, C. and Lyubeznik, G., On the vanishing of local cohomology modules, Invent. Math. 102 (1990), 73–93.Google Scholar
Katzman, M., Lyubeznik, G. and Zhang, W., An extension of a theorem of Hartshorne, Proc. Amer. Math. Soc., to appear, arXiv:1408.0858.Google Scholar
Kollár, J., Grothendieck–Lefschetz type theorems for the local Picard group, J. Ramanujan Math. Soc. 28A (2013), 267–285.Google Scholar
Kollár, J., Maps between local Picard groups, Preprint (2014), arXiv:1407.5108.Google Scholar
Lyubeznik, G., Finiteness properties of local cohomology modules, Invent. Math. 113 (1993), 41–55.CrossRefGoogle Scholar
Lyubeznik, G., On the vanishing of local cohomology in characteristic p > 0, Compositio Math. 142 (2006), 207–221.CrossRefGoogle Scholar
Lyubeznik, G., On some local cohomology modules, Adv. Math. 213 (2007), 621–643.Google Scholar
Ogus, A., Local cohomological dimension, Ann. of Math. (2) 98 (1973), 327–365.Google Scholar
Peskine, C. and Szpiro, L., Dimension projective finie et cohomologie locale, Publ. Math. Inst. Hautes Et́udes Sci. 42 (1973), 47–119.Google Scholar
Varbaro, M., Cohomological and projective dimensions, Compositio Math. 149 (2013), 1203–1210.Google Scholar