Axisymmetric numerical simulations of the hydrodynamics around rising bubbles are performed in order to investigate the impact of surfactants on the bubble dynamics. Surfactants are assumed to be insoluble. The transport of the adsorbed surfactants is computed along the deforming surface at large surface Péclet number, and Marangoni stresses are taken into account. This simulation model leads to the stagnant-cap regime, with partially immobile interfaces. A parametric study is performed on cases at given Archimedes number, by varying the degree of contamination (Marangoni number) but maintaining a nearly constant Eötvös number. The presence of surfactants affects the rise velocity for oblate bubbles less than for spherical bubbles: the increase of the drag coefficient, due to interface contamination, is mitigated by a lower bubble deformation. When the cap angle 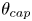$\theta _{cap}$ belongs to the southern hemisphere, the aspect ratio 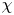$\chi$ is found to decrease with contamination: the dynamic pressure responsible for the bubble distortion is lowered, related to the decline of kinetic energy. As soon as 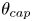$\theta _{cap}$ lies in the northern hemisphere, the pressure stress causing distortion becomes independent on 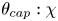$\theta _{cap}: \chi$ no longer evolves with contamination, and already matches the prediction for fully immobile interfaces. Mass transfer of a passive scalar across the contaminated interface is also analysed. Surprisingly, the Sherwood number 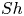$Sh$ is found to follow the same law as for spherical shapes (Kentheswaran et al., Intl J. Heat Mass Transfer, vol. 198, 2022, 123325), allowing us to predict the decrease in 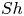$Sh$ due to contamination. These results reveal the couplings between interface immobilisation, bubble deformation, rise velocity and interfacial mass transfer.

This paper studies numerically the convection of water vapour in snowpacks using an Eulerian–Eulerian two-phase approach. The convective water vapour transport in snow and its effects on snow density are often invoked to explain observed density profiles, e.g. of thin Arctic snow covers, but this process has never been numerically simulated and analysed in a systematic manner. Here, the impact of convection on the thermal and phase change regimes as a function of different snowpack depths, thermal boundary conditions and Rayleigh numbers is analysed. We find considerable impact of natural convection on the snow density distribution with a layer of significantly lower density at the bottom of the snowpack and a layer of higher density located higher in the snowpack or at the surface. We find that emergent heterogeneity in the snow porosity results in a feedback effect on the spatial organization of convection cells causing their horizontal displacement. Regions where the snowpack is most impacted by phase changes are found to be horizontally extended and vertically thin, ‘pancake’-like layers at the top and bottom of the snowpack. We further demonstrate that among the parameters important for natural convection, the snowpack depth has the strongest influence on the heat and mass transfer. Despite our simplifying assumptions, our study represents a significant improvement over the state of the art and a first step to accurately simulate snowpack dynamics in diverse regions of the cryosphere.

In this paper, we will use optimal mass transport combining with suitable transforms to study the sharp constants and optimizers for a class of the Gagliardo–Nirenberg and Caffarelli–Kohn–Nirenberg inequalities. Moreover, we will investigate these inequalities with and without the monomial weights $x_{1}^{A_{1}} \cdots x_{N}^{A_{N}}$ on ℝN.

The lobe dynamics andmass transport between separation bubble and main flow in flow over airfoil are studied in detail, using Lagrangian coherent structures (LCSs), in order to understand the nature of evolution of the separation bubble. For this problem, the transient flow over NACA0012 airfoil with low Reynolds number is simulated numerically by characteristic based split (CBS) scheme, in combination with dual time stepping. Then, LCSs and lobe dynamics are introduced and developed to investigate themass transport between separation bubble and main flow, from viewpoint of nonlinear dynamics. The results show that stable manifolds and unstable manifolds could be tangled with each other as time evolution, and the lobes are formed periodically to induce mass transport between main flow and separation bubble, with dynamic behaviors. Moreover, the evolution of the separation bubble depends essentially on the mass transport which is induced by lobes, ensuing energy and momentum transfers. As the results, it can be drawn that the dynamics of flow separation could be studied using LCSs and lobe dynamics, and could be controlled feasibly if an appropriate control is applied to the upstream boundary layer with high momentum.

Mass transport within collagen-based matrices is critical to tissue development, repair, and pathogenesis, as well as the design of next-generation tissue engineering strategies. This work shows how collagen precursors, specified by intermolecular cross-link composition, provide independent control of collagen matrix mechanical and transport properties. Collagen matrices were prepared from tissue-extracted monomers or oligomers. Viscoelastic behavior was measured in oscillatory shear and unconfined compression. Matrix permeability and diffusivity were measured using gravity-driven permeametry and integrated optical imaging, respectively. Both collagen types showed an increase in stiffness and permeability hindrance with increasing collagen concentration (fibril density); however, different physical property–concentration relationships were noted. Diffusivity was not affected by concentration for either collagen type over the range tested. In general, oligomer matrices exhibited a substantial increase in stiffness and only a modest decrease in transport properties when compared with monomer matrices prepared at the same concentration. The observed differences in viscoelastic and transport properties were largely attributed to increased levels of interfibril branching within oligomer matrices. The ability to relate physical properties to relevant microstructure parameters, including fibril density and interfibril branching, is expected to advance the understanding of cell–matrix signaling, as well as facilitate model-based prediction and design of matrix-based therapeutic strategies.

In this paper, weconsider probability measures μ and ν on a d-dimensionalsphere in ${\bf R}^{d+1}, d \geq 1,$ and cost functions of the form $c({\bf x},{\bf y})=l(\frac{|{\bf x}-{\bf y}|^2}{2})$ that generalize those arising in geometric optics where $l(t)=-\log t.$ We prove that if μ and ν vanish on $(d-1)$ -rectifiable sets,if |l'(t)|>0, $\lim_{t\rightarrow 0^+}l(t)=+\infty,$ and $g(t):=t(2-t)(l'(t))^2$ is monotone then thereexists a unique optimal map T o that transports μ onto $\nu,$ whereoptimality is measured against c. Furthermore, $\inf_{{\bf x}}|T_o{\bf x}-{\bf x}|>0.$ Our approach is based on direct variational arguments.In the special case when $l(t)=-\log t,$ existence of optimal maps on thesphere was obtained earlier in [Glimm and Oliker, J. Math. Sci.117 (2003) 4096-4108]and [Wang, Calculus of Variations and PDE's20 (2004) 329-341] under more restrictive assumptions. In these studies, it was assumed that either μ and ν are absolutelycontinuous with respect to the d-dimensional Haussdorff measure, or they have disjoint supports. Another aspect of interestin this work is that it is in contrast with the work in[Gangbo and McCann, Quart. Appl. Math.58 (2000) 705-737] where it is proved that when l(t)=t thenexistence of an optimal map fails when μ and ν are supported by Jordan surfaces.

This article is an edited transcript based on the David Turnbull Lecture given by Ellen D. Williams of the University of Maryland on December 2, 2003, at the Materials Research Society Fall Meeting in Boston.Williams received the award for “groundbreaking research on the atomic-scale science of surfaces and for leadership, writing, teaching, and outreach that convey her deep understanding of and enthusiasm for materials research.” This article focuses on the special properties of small structures that provide much of the exciting potential of nanotechnology.One aspect of small structures—their susceptibility to thermal fluctuations—may create or necessitate new ways of exploiting nanostructures.The advent of scanned probe imaging techniques created new opportunities for observing and understanding such structural fluctuations and the related evolution of nanostructure.Direct observations show that it is relatively easy for large numbers of atoms—the kinds of numbers that are present in nanoscale structures—to pick up and move about on the surface cooperatively with substantial impact on nano-to micron-scale structures.Such labile evolution of structure can be predicted quantitatively by using length-scale bridging techniques of statistical mechanics coupled with scanned probe observations of structural and temporal distributions.The same measurements also provide direct information about the stochastic paths of structural fluctuations that can be used outside of the traditional thermodynamic framework.Future work involves moving beyond the classical thermodynamic picture to assess the impact that the stochastic behavior has on the physical properties of individual nanostructures.

We study the dispersion of a collection of particles carried by an isotropic Brownian flow in Of particular interest are the center of mass and the centered spatial second moments. Their asymptotic behavior depends strongly on the spatial dimension and the largest Lyapunov exponent of the flow. We use estimates for the pair separation process to give a fairly complete picture of this behavior as t → ∞. In particular, for incompressible flows in two dimensions, we show that the variance of the center of mass grows sublinearly, while dispersion relative to the center of mass grows linearly.