Published online by Cambridge University Press: 29 August 2023
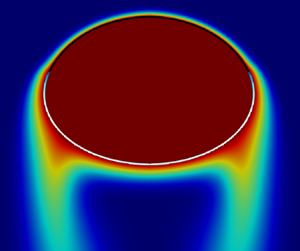
Axisymmetric numerical simulations of the hydrodynamics around rising bubbles are performed in order to investigate the impact of surfactants on the bubble dynamics. Surfactants are assumed to be insoluble. The transport of the adsorbed surfactants is computed along the deforming surface at large surface Péclet number, and Marangoni stresses are taken into account. This simulation model leads to the stagnant-cap regime, with partially immobile interfaces. A parametric study is performed on cases at given Archimedes number, by varying the degree of contamination (Marangoni number) but maintaining a nearly constant Eötvös number. The presence of surfactants affects the rise velocity for oblate bubbles less than for spherical bubbles: the increase of the drag coefficient, due to interface contamination, is mitigated by a lower bubble deformation. When the cap angle  $\theta _{cap}$ belongs to the southern hemisphere, the aspect ratio
$\theta _{cap}$ belongs to the southern hemisphere, the aspect ratio  $\chi$ is found to decrease with contamination: the dynamic pressure responsible for the bubble distortion is lowered, related to the decline of kinetic energy. As soon as
$\chi$ is found to decrease with contamination: the dynamic pressure responsible for the bubble distortion is lowered, related to the decline of kinetic energy. As soon as  $\theta _{cap}$ lies in the northern hemisphere, the pressure stress causing distortion becomes independent on
$\theta _{cap}$ lies in the northern hemisphere, the pressure stress causing distortion becomes independent on  $\theta _{cap}: \chi$ no longer evolves with contamination, and already matches the prediction for fully immobile interfaces. Mass transfer of a passive scalar across the contaminated interface is also analysed. Surprisingly, the Sherwood number
$\theta _{cap}: \chi$ no longer evolves with contamination, and already matches the prediction for fully immobile interfaces. Mass transfer of a passive scalar across the contaminated interface is also analysed. Surprisingly, the Sherwood number  $Sh$ is found to follow the same law as for spherical shapes (Kentheswaran et al., Intl J. Heat Mass Transfer, vol. 198, 2022, 123325), allowing us to predict the decrease in
$Sh$ is found to follow the same law as for spherical shapes (Kentheswaran et al., Intl J. Heat Mass Transfer, vol. 198, 2022, 123325), allowing us to predict the decrease in  $Sh$ due to contamination. These results reveal the couplings between interface immobilisation, bubble deformation, rise velocity and interfacial mass transfer.
$Sh$ due to contamination. These results reveal the couplings between interface immobilisation, bubble deformation, rise velocity and interfacial mass transfer.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.