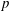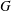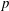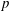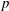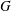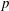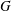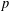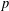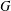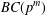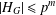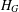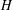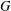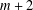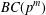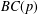Refine search
Actions for selected content:
5 results
Character Codegrees of Maximal Class
 $p$-groups
$p$-groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 25 September 2019, pp. 328-334
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
FINITE
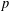 $p$-GROUPS ALL OF WHOSE NONNORMAL SUBGROUPS HAVE BOUNDED NORMAL CORES
$p$-GROUPS ALL OF WHOSE NONNORMAL SUBGROUPS HAVE BOUNDED NORMAL CORES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 255-265
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
COHOMOLOGY OF FILIFORM LIE ALGEBRAS OVER FIELDS OF CHARACTERISTIC TWO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 168-170
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
AUTOMORPHISMS OF METABELIAN PRIME POWER ORDER GROUPS OF MAXIMAL CLASS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 261-276
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
The Modular Group Algebra Problem for Small p-Groups Of Maximal Class
-
- Journal:
- Canadian Journal of Mathematics / Volume 48 / Issue 5 / 01 October 1996
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1064-1078
- Print publication:
- 01 October 1996
-
- Article
-
- You have access
- Export citation