We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We construct new optimal 
$L^{p}$ Hardy-type inequalities for elliptic Schrödinger-type operators with a potential term.
Let Ω be an open connected cone in ℝn with vertex at the origin. Assume that the Operator
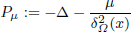
is subcritical in Ω, where δΩ is the distance function to the boundary of Ω and μ ⩽ 1/4. We show that under some smoothness assumption on Ω the improved Hardy-type inequality
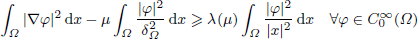
holds true, and the Hardy-weight λ(μ)|x|–2 is optimal in a certain definite sense. The constant λ(μ) > 0 is given explicitly.
