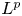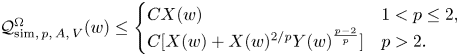1. Introduction
For any ![]() $\xi \in \mathbb {R}^{n}$ and a positive definite matrix
$\xi \in \mathbb {R}^{n}$ and a positive definite matrix ![]() $A\in \mathbb {R}^{n \times n}$, let
$A\in \mathbb {R}^{n \times n}$, let ![]() $| \xi |_A:=\sqrt {\langle A\xi,\,\xi \rangle }$, where
$| \xi |_A:=\sqrt {\langle A\xi,\,\xi \rangle }$, where ![]() $\langle \cdot,\, \cdot \rangle$ denotes the Euclidean inner product on
$\langle \cdot,\, \cdot \rangle$ denotes the Euclidean inner product on ![]() $\mathbb {R}^{n}$. Consider a second order half-linear operator of the form
$\mathbb {R}^{n}$. Consider a second order half-linear operator of the form
defined in a domain ![]() $\Omega \subset \mathbb {R}^{n}$,
$\Omega \subset \mathbb {R}^{n}$, ![]() $n\geq 2$, and assume that the equation
$n\geq 2$, and assume that the equation ![]() $Q_{p,A,V}(u)=0$ admits a positive solution in
$Q_{p,A,V}(u)=0$ admits a positive solution in ![]() $\Omega$. We are interested to find an optimal weight function
$\Omega$. We are interested to find an optimal weight function ![]() $W\gneqq 0$ (see definition 2.29) such that the equation
$W\gneqq 0$ (see definition 2.29) such that the equation ![]() $Q_{p,A,V-W}(u)=0$ admits a positive solution in
$Q_{p,A,V-W}(u)=0$ admits a positive solution in ![]() $\Omega$. Equivalently [Reference Pinchover and Psaradakis19, theorem 4.3], we are interested to find an optimal weight function
$\Omega$. Equivalently [Reference Pinchover and Psaradakis19, theorem 4.3], we are interested to find an optimal weight function ![]() $W\gneqq 0$ such that the following Hardy-type inequality is satisfied:
$W\gneqq 0$ such that the following Hardy-type inequality is satisfied:
In some definite sense, an optimal weight ![]() $W\gneqq 0$ is ‘as large as possible’ nonnegative function such that (1.1) is satisfied for all nonnegative
$W\gneqq 0$ is ‘as large as possible’ nonnegative function such that (1.1) is satisfied for all nonnegative ![]() $\phi \in {C_0^{\infty }(\Omega )}$.
$\phi \in {C_0^{\infty }(\Omega )}$.
The search for Hardy-type inequalities with optimal weight function ![]() $W$ was originally proposed by Agmon, who raised this problem in connection with his theory of exponential decay of Schrödinger eigenfunctions [Reference Agmon1, p. 6]. In the past four decades, the problem of improving Hardy-type inequalities has engaged many authors. In particular, Hardy-type inequalities were established for a vast class of operators (e.g., elliptic operators, Schrödinger operators on graphs, fractional differential equations) with different types of boundary conditions, see [Reference Balinsky, Evans and Lewis2–Reference Bogdan and Dyda4, Reference Brezis and Marcus6, Reference Devyver, Fraas and Pinchover8–Reference Ekholm, Kovařík and Laptev10, Reference Keller, Pinchover and Pogorzelski14, Reference Pinchover and Versano22]. In [Reference Devyver and Pinchover9], Devyver and Pinchover studied the problem of optimal weights for the operator
$W$ was originally proposed by Agmon, who raised this problem in connection with his theory of exponential decay of Schrödinger eigenfunctions [Reference Agmon1, p. 6]. In the past four decades, the problem of improving Hardy-type inequalities has engaged many authors. In particular, Hardy-type inequalities were established for a vast class of operators (e.g., elliptic operators, Schrödinger operators on graphs, fractional differential equations) with different types of boundary conditions, see [Reference Balinsky, Evans and Lewis2–Reference Bogdan and Dyda4, Reference Brezis and Marcus6, Reference Devyver, Fraas and Pinchover8–Reference Ekholm, Kovařík and Laptev10, Reference Keller, Pinchover and Pogorzelski14, Reference Pinchover and Versano22]. In [Reference Devyver and Pinchover9], Devyver and Pinchover studied the problem of optimal weights for the operator ![]() $Q_{p,A,V}$. However, they managed to find optimal weights only in the case where
$Q_{p,A,V}$. However, they managed to find optimal weights only in the case where ![]() $A$ is the identity matrix and
$A$ is the identity matrix and ![]() $V=0$. They proved (under certain assumptions) that the
$V=0$. They proved (under certain assumptions) that the ![]() $p$-Laplace operator,
$p$-Laplace operator, ![]() $-\mathrm {div}(|\nabla u|^{p-2}\nabla u )$, admits an optimal Hardy-weight. More specifically, it is proved that if
$-\mathrm {div}(|\nabla u|^{p-2}\nabla u )$, admits an optimal Hardy-weight. More specifically, it is proved that if ![]() $1< p\leq n$, then
$1< p\leq n$, then ![]() $W= ( \frac {p-1}{p})^{p}\left | \frac {\nabla G}{G}\right |^{p}$ an optimal Hardy-weight, where
$W= ( \frac {p-1}{p})^{p}\left | \frac {\nabla G}{G}\right |^{p}$ an optimal Hardy-weight, where ![]() $G$ is the associated positive minimal Green function with singularity at
$G$ is the associated positive minimal Green function with singularity at ![]() $0$. For
$0$. For ![]() $p>n$, several cases should be considered, depending on the behaviour of a positive
$p>n$, several cases should be considered, depending on the behaviour of a positive ![]() $p$-harmonic function with singularity at
$p$-harmonic function with singularity at ![]() $0$.
$0$.
In the present paper we make a nontrivial progress towards the study of (1.1) in the case where ![]() $A$ is not necessarily the identity matrix, and
$A$ is not necessarily the identity matrix, and ![]() $V$ is a slowly growing potential function. Our main result reads as follows.
$V$ is a slowly growing potential function. Our main result reads as follows.
Theorem 1.1 Let ![]() $\Omega \subset \mathbb {R}^{n},$
$\Omega \subset \mathbb {R}^{n},$ ![]() $n\geq 2,$ be a domain and
$n\geq 2,$ be a domain and ![]() $x_0\in \Omega$. Let
$x_0\in \Omega$. Let ![]() $Q_{p,A,V}$ be a subcritical operator in
$Q_{p,A,V}$ be a subcritical operator in ![]() $\Omega$ satisfying assumptions 2.8 in
$\Omega$ satisfying assumptions 2.8 in ![]() $\Omega$. Suppose that
$\Omega$. Suppose that ![]() $Q_{p,A,V}$ admits a (nonnegative) Green potential,
$Q_{p,A,V}$ admits a (nonnegative) Green potential, ![]() $G_{\varphi }(x)$, in
$G_{\varphi }(x)$, in ![]() $\Omega$ (see definition 2.22) satisfying
$\Omega$ (see definition 2.22) satisfying
where ![]() $\overline {\infty }$ denotes the ideal point in the one-point compactification of
$\overline {\infty }$ denotes the ideal point in the one-point compactification of ![]() $\Omega$. Then the operator
$\Omega$. Then the operator ![]() $Q_{p,A,{V}/{c_p}}$ admits an optimal Hardy-weight in
$Q_{p,A,{V}/{c_p}}$ admits an optimal Hardy-weight in ![]() $\Omega,$ where
$\Omega,$ where ![]() $c_p=(p/ (p-1))^{p-1}$.
$c_p=(p/ (p-1))^{p-1}$.
As a corollary of the proof of theorem 1.1 we obtain the following result.
Corollary 1.2 Let ![]() $\Omega \subset \mathbb {R}^{n},$
$\Omega \subset \mathbb {R}^{n},$ ![]() $n\geq 2,$ be a domain and
$n\geq 2,$ be a domain and ![]() $x_0\in K\Subset \Omega$. Let
$x_0\in K\Subset \Omega$. Let ![]() $Q_{p,A,V}$ be a subcritical operator in
$Q_{p,A,V}$ be a subcritical operator in ![]() $\Omega$ satisfying assumptions 2.8 with
$\Omega$ satisfying assumptions 2.8 with ![]() $V\leq 0$ in
$V\leq 0$ in ![]() $\Omega$. Suppose that
$\Omega$. Suppose that ![]() $Q_{p,A,V}$ admits a positive minimal Green function
$Q_{p,A,V}$ admits a positive minimal Green function ![]() $G(x)$ in
$G(x)$ in ![]() $\Omega \setminus \{x_0\}$ (see definition 2.22) satisfying
$\Omega \setminus \{x_0\}$ (see definition 2.22) satisfying
where ![]() $\overline {\infty }$ denotes the ideal point in the one-point compactification of
$\overline {\infty }$ denotes the ideal point in the one-point compactification of ![]() $\Omega$. Then the operator
$\Omega$. Then the operator ![]() $Q_{p,A,{V}/{c_p}}$ admits an optimal Hardy-weight in
$Q_{p,A,{V}/{c_p}}$ admits an optimal Hardy-weight in ![]() $\Omega,$ where
$\Omega,$ where ![]() $c_p=(p/ (p-1))^{p-1}$.
$c_p=(p/ (p-1))^{p-1}$.
The paper is organized as follows. In § 2, we introduce the necessary notation and recall some previously obtained results needed in the present paper. We proceed in § 3, with proving essential results needed for the proof of theorem 1.1, and then we prove theorem 1.1 and corollary 1.2.
2. Preliminaries
Let ![]() $\Omega \subset \mathbb {R}^{n}$ be a domain, and let
$\Omega \subset \mathbb {R}^{n}$ be a domain, and let ![]() $1< p<\infty$. Throughout the paper we use the following notation and conventions:
$1< p<\infty$. Throughout the paper we use the following notation and conventions:
• For any
 $R>0$ and
$R>0$ and  $x\in \mathbb {R}^{n}$, we denote by
$x\in \mathbb {R}^{n}$, we denote by  $B_R(x)$ the open ball of radius
$B_R(x)$ the open ball of radius  $R$ centred at
$R$ centred at  $x$, and
$x$, and  $B_R^{+}(0)=\{x\in B_R(0) : x_n > 0\}$.
$B_R^{+}(0)=\{x\in B_R(0) : x_n > 0\}$.• We write
 $\Omega _1 \Subset \Omega _2$ if
$\Omega _1 \Subset \Omega _2$ if  $\Omega _2$ is open in
$\Omega _2$ is open in  $\Omega,$ the set
$\Omega,$ the set  $\overline {\Omega _1}$ is compact, and
$\overline {\Omega _1}$ is compact, and  $\overline {\Omega _1}\subset \Omega _2$.
$\overline {\Omega _1}\subset \Omega _2$.•
 $C$ refers to a positive constant which may vary from line to line.
$C$ refers to a positive constant which may vary from line to line.• Let
 $g_1,\,g_2$ be two positive functions defined in
$g_1,\,g_2$ be two positive functions defined in  $\Omega$. We use the notation
$\Omega$. We use the notation  $g_1\asymp g_2$ in
$g_1\asymp g_2$ in  $\Omega$ if there exists a positive constant
$\Omega$ if there exists a positive constant  $C$ such that
$C$ such that
 \[ C^{{-}1}g_{2}(x)\leq g_{1}(x) \leq Cg_{2}(x) \qquad \mbox{ for all } x\in \Omega. \]
\[ C^{{-}1}g_{2}(x)\leq g_{1}(x) \leq Cg_{2}(x) \qquad \mbox{ for all } x\in \Omega. \]• Let
 $g_1,\,g_2$ be two positive functions defined in
$g_1,\,g_2$ be two positive functions defined in  $\Omega$, and let
$\Omega$, and let  $x_0\in \Omega$. We use the notation
$x_0\in \Omega$. We use the notation  $g_1\sim g_2$ near
$g_1\sim g_2$ near  $x_0$ if there exists a positive constant
$x_0$ if there exists a positive constant  $C$ such that
$C$ such that
 \[ \lim_{x\to x_0}\frac{g_1(x)}{g_2(x)}=C. \]
\[ \lim_{x\to x_0}\frac{g_1(x)}{g_2(x)}=C. \]• The gradient of a function
 $f$ will be denoted by
$f$ will be denoted by  $\nabla f$.
$\nabla f$.•
 $\chi _B$ denotes the characteristic function of a set
$\chi _B$ denotes the characteristic function of a set  $B\subset \mathbb {R}^{n}$.
$B\subset \mathbb {R}^{n}$.• For any
 $1\leq p\leq \infty$,
$1\leq p\leq \infty$,  $p'$ is the Hölder conjugate exponent of
$p'$ is the Hölder conjugate exponent of  $p$ satisfying
$p$ satisfying  $p'=p/ (p-1)$.
$p'=p/ (p-1)$.• For
 $1\leq p< n$,
$1\leq p< n$,  $p^{*}:=np/(n-p)$ is its Sobolev critical exponent.
$p^{*}:=np/(n-p)$ is its Sobolev critical exponent.• For a real valued function
 $W$, we write
$W$, we write  $W\gneqq 0$ in
$W\gneqq 0$ in  $\Omega$ if
$\Omega$ if  $W\geq 0$ in
$W\geq 0$ in  $\Omega$ and
$\Omega$ and  $\sup \limits _{\Omega }W>0$.
$\sup \limits _{\Omega }W>0$.• For a symmetric positive definite
 $A\in L_{\textrm {loc}}^{\infty }(\Omega,\,\mathbb {R}^{n\times n})$, we denote
$A\in L_{\textrm {loc}}^{\infty }(\Omega,\,\mathbb {R}^{n\times n})$, we denote  $\Delta _{p,A} (u):=\mathrm {div}(|\nabla u|_A^{p-2}A\nabla u)$ is the
$\Delta _{p,A} (u):=\mathrm {div}(|\nabla u|_A^{p-2}A\nabla u)$ is the  $(p,\,A)$-Laplace operator.
$(p,\,A)$-Laplace operator.• For a real valued function
 $u$ and
$u$ and  $1< p<\infty$,
$1< p<\infty$,  $\mathcal {I}_p(u):=|u|^{p-2}u$.
$\mathcal {I}_p(u):=|u|^{p-2}u$.•
 $\overline {\infty }$ denotes the ideal point in the one-point compactification of
$\overline {\infty }$ denotes the ideal point in the one-point compactification of  $\Omega$.
$\Omega$.•
 $\mathbb {R}_+$ denotes the interval
$\mathbb {R}_+$ denotes the interval  $(0,\,\infty )$.
$(0,\,\infty )$.•
 $d_{\Omega }=\mathrm {dist}(\cdot,\,\partial \Omega ):\Omega \to (0,\,\infty )$ is the distance function to
$d_{\Omega }=\mathrm {dist}(\cdot,\,\partial \Omega ):\Omega \to (0,\,\infty )$ is the distance function to  $\partial \Omega$.
$\partial \Omega$.•
 $\mathrm {diam}(\Omega )$ denotes the diameter of
$\mathrm {diam}(\Omega )$ denotes the diameter of  $\Omega$.
$\Omega$.•
 $\mathrm {supp} (u)$ denotes the support of the function
$\mathrm {supp} (u)$ denotes the support of the function  $u$.
$u$.•
 $\mathcal {H}^{l}$,
$\mathcal {H}^{l}$,  $1\leq l \leq n$, denotes the
$1\leq l \leq n$, denotes the  $l$-dimensional Hausdorff measure on
$l$-dimensional Hausdorff measure on  $\mathbb {R}^{n}$.
$\mathbb {R}^{n}$.
2.1 Gauss–Green formula
We continue with several definitions and results concerning the Gauss–Green theorem [Reference Chen, Torres and Ziemer7].
Definition 2.1 Let ![]() $D\subset \mathbb {R}^{n}$ be an open set.
$D\subset \mathbb {R}^{n}$ be an open set.
(i) We denote by
 $\mathcal {M}(D)$ the space of all signed Radon measures
$\mathcal {M}(D)$ the space of all signed Radon measures  $\mu$ on
$\mu$ on  $D$ such that
$D$ such that  $\int _{D}\,\text {d}|\mu |<\infty$.
$\int _{D}\,\text {d}|\mu |<\infty$.(ii) A vector field
 $F\in L^{\infty }(D,\,\mathbb {R}^{n})$ is called a divergence measure field, written as
$F\in L^{\infty }(D,\,\mathbb {R}^{n})$ is called a divergence measure field, written as  $F\in \mathcal {DM}^{\infty }(D)$, if
$F\in \mathcal {DM}^{\infty }(D)$, if  $\mathrm {div}(F)=\mu \in \mathcal {M}(D)$, i.e., there exists
$\mathrm {div}(F)=\mu \in \mathcal {M}(D)$, i.e., there exists  $\mu \in \mathcal {M}(D)$ such that
$\mu \in \mathcal {M}(D)$ such that
 \[ \int_D \phi \,\mathrm{d}\mu={-}\int_{D}\nabla \phi \cdot F \,\mathrm{d}x \quad \forall\, \phi\in C_0^{\infty}(D). \]
\[ \int_D \phi \,\mathrm{d}\mu={-}\int_{D}\nabla \phi \cdot F \,\mathrm{d}x \quad \forall\, \phi\in C_0^{\infty}(D). \](iii) We say that a vector field
 $F\in L^{\infty }_{{\textrm {loc}}}(D,\,\mathbb {R}^{n})$ belongs to
$F\in L^{\infty }_{{\textrm {loc}}}(D,\,\mathbb {R}^{n})$ belongs to  $\mathcal {DM}^{\infty }_{{\textrm {loc}}}(D)$ if for any open subset
$\mathcal {DM}^{\infty }_{{\textrm {loc}}}(D)$ if for any open subset  $E\Subset D$, we have
$E\Subset D$, we have  $F\in \mathcal {DM}^{\infty }(E)$.
$F\in \mathcal {DM}^{\infty }(E)$.
Definition 2.2 cf. [Reference Chen, Torres and Ziemer7] and [Reference Evans and Gariepy11, section 5]
Let ![]() $D\subset \mathbb {R}^{n}$ be an open set. A function
$D\subset \mathbb {R}^{n}$ be an open set. A function ![]() $f\in L^{1}(D)$ has a bounded variation in
$f\in L^{1}(D)$ has a bounded variation in ![]() $D$ if
$D$ if
Denote by ![]() $\mathrm {BV}(D)$ the space of all functions
$\mathrm {BV}(D)$ the space of all functions ![]() $f\in L^{1}(D)$ having bounded variation.
$f\in L^{1}(D)$ having bounded variation.
Definition 2.3 Let ![]() $D\subset \mathbb {R}^{n}$ be an open set. A measurable subset
$D\subset \mathbb {R}^{n}$ be an open set. A measurable subset ![]() $E\subset \mathbb {R}^{n}$ is said to be a set of finite perimeter in
$E\subset \mathbb {R}^{n}$ is said to be a set of finite perimeter in ![]() $D$ if
$D$ if ![]() $\chi _E\in \mathrm {BV}(D)$.
$\chi _E\in \mathrm {BV}(D)$.
Proposition 2.4 [Reference Evans and Gariepy11, theorem 5.9, p. 212]
Let ![]() $E\Subset \mathbb {R}^{n}$ and let
$E\Subset \mathbb {R}^{n}$ and let ![]() $0\leq f\in \mathrm {BV}(E)\cap C^{1}(E)$. Then, for a.e.
$0\leq f\in \mathrm {BV}(E)\cap C^{1}(E)$. Then, for a.e. ![]() $t\in [0,\,\infty )$ the set
$t\in [0,\,\infty )$ the set ![]() $\{x\in E: f(x)>t\}$ has finite perimeter. In particular, for a.e.
$\{x\in E: f(x)>t\}$ has finite perimeter. In particular, for a.e. ![]() $0\leq t_1< t_2$ the set
$0\leq t_1< t_2$ the set ![]() $\{x\in E: t_1< f(x)< t_2\}$ has finite perimeter.
$\{x\in E: t_1< f(x)< t_2\}$ has finite perimeter.
We proceed with the following Gauss–Green theorem of divergence measure fields over sets of finite perimeter (see [Reference Chen, Torres and Ziemer7, theorems 5.2 and 7.2] and [Reference Devyver and Pinchover9, proposition 3.1]).
Lemma 2.5 Let ![]() $D\subset \mathbb {R}^{n}$ be an open set. Suppose that
$D\subset \mathbb {R}^{n}$ be an open set. Suppose that ![]() $F\in \mathcal {DM}^{\infty }_{{\textrm {loc}}}(D)$ with
$F\in \mathcal {DM}^{\infty }_{{\textrm {loc}}}(D)$ with ![]() $\mathrm {div}(F)=\mu \in \mathcal {M}(D)$. Let
$\mathrm {div}(F)=\mu \in \mathcal {M}(D)$. Let ![]() $E\Subset D$ be a set of finite perimeter satisfying
$E\Subset D$ be a set of finite perimeter satisfying
•
 $\partial E=(\bigcup \limits _{k\in \mathbb {N}}D_k) \cup N,$
$\partial E=(\bigcup \limits _{k\in \mathbb {N}}D_k) \cup N,$• for each
 $k\in \mathbb {N},$
$k\in \mathbb {N},$  $D_k$ is
$D_k$ is  $(n-1)$- dimensional
$(n-1)$- dimensional  $C^{1}$ surface, and
$C^{1}$ surface, and  $\mathcal {H}^{n-1}(N)=0$.
$\mathcal {H}^{n-1}(N)=0$.
Then,
where ![]() $\vec {n}$ is a classical outer unit normal to
$\vec {n}$ is a classical outer unit normal to ![]() $\partial E$ which is defined
$\partial E$ which is defined ![]() $\mathcal {H}^{n-1}$-a.e. on
$\mathcal {H}^{n-1}$-a.e. on ![]() $\partial E$.
$\partial E$.
2.2 Local Morrey spaces
In the present subsection we introduce a certain class of Morrey spaces that depend on the index ![]() $p$, where
$p$, where ![]() $1< p<\infty$.
$1< p<\infty$.
Definition 2.6 Let ![]() $q\in [1,\,\infty ]$ and
$q\in [1,\,\infty ]$ and ![]() $\omega \Subset \mathbb {R}^{n}$. For a measurable, real valued function
$\omega \Subset \mathbb {R}^{n}$. For a measurable, real valued function ![]() $f$ defined in
$f$ defined in ![]() $\omega$, we set
$\omega$, we set
 \[ \|f\|_{M^{q}(\omega)}:= \sup_{\substack{y\in \omega\\ r<\mathrm{diam}(\omega)}} \frac{1}{r^{n/q'}}\int_{\omega\cap B_r(y)}|f| \,\mathrm{d}x. \]
\[ \|f\|_{M^{q}(\omega)}:= \sup_{\substack{y\in \omega\\ r<\mathrm{diam}(\omega)}} \frac{1}{r^{n/q'}}\int_{\omega\cap B_r(y)}|f| \,\mathrm{d}x. \]
We write ![]() $f\in M^{q}_{{\textrm {loc}}}(\Omega )$ if for any
$f\in M^{q}_{{\textrm {loc}}}(\Omega )$ if for any ![]() $\omega \Subset \Omega$ we have
$\omega \Subset \Omega$ we have ![]() $\|f\|_{M^{q}(\omega )}<\infty$.
$\|f\|_{M^{q}(\omega )}<\infty$.
Next, we define a special local Morrey space ![]() $M^{q}_{{\textrm {loc}}}(p;\Omega )$ which depends on the values of the exponent
$M^{q}_{{\textrm {loc}}}(p;\Omega )$ which depends on the values of the exponent ![]() $p$.
$p$.
Definition 2.7 For ![]() $p\neq n$, we define
$p\neq n$, we define
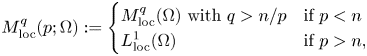 \[ M^{q}_{{\textrm{loc}}}(p;\Omega):= \begin{cases} M^{q}_{{\textrm{loc}}}(\Omega) \text{ with } q>n/p & \text{if } p< n \\ L^{1}_{{\textrm{loc}}}(\Omega) & \text{if } p>n, \end{cases} \]
\[ M^{q}_{{\textrm{loc}}}(p;\Omega):= \begin{cases} M^{q}_{{\textrm{loc}}}(\Omega) \text{ with } q>n/p & \text{if } p< n \\ L^{1}_{{\textrm{loc}}}(\Omega) & \text{if } p>n, \end{cases} \]
while for ![]() $p=n$,
$p=n$, ![]() $f\in M^{q}_{{\textrm {loc}}}(n;\Omega )$ means that for some
$f\in M^{q}_{{\textrm {loc}}}(n;\Omega )$ means that for some ![]() $q>n$ and any
$q>n$ and any ![]() $\omega \Subset \Omega$ we have
$\omega \Subset \Omega$ we have
 \[ \|f\|_{M^{q}_{n;\omega}}:= \sup_{\substack{y\in \omega\\ r<\mathrm{diam}(\omega)}} \varphi_q(r)\int_{\omega\cap B_r(y)}|f| \,\mathrm{d}x<\infty, \]
\[ \|f\|_{M^{q}_{n;\omega}}:= \sup_{\substack{y\in \omega\\ r<\mathrm{diam}(\omega)}} \varphi_q(r)\int_{\omega\cap B_r(y)}|f| \,\mathrm{d}x<\infty, \]
where ![]() $\varphi _q(r):=\log (\mathrm {diam}(\omega )/r)^{q/n'}$ and
$\varphi _q(r):=\log (\mathrm {diam}(\omega )/r)^{q/n'}$ and ![]() $0< r<\mathrm {diam}(\omega )$.
$0< r<\mathrm {diam}(\omega )$.
For the regularity theory of equations with coefficients in Morrey spaces we refer the reader to [Reference Malý and Ziemer18, Reference Pinchover and Psaradakis19].
We associate to any domain ![]() $\Omega \subset \mathbb {R}^{n}$ an exhaustion, i.e. a sequence of smooth, precompact domains
$\Omega \subset \mathbb {R}^{n}$ an exhaustion, i.e. a sequence of smooth, precompact domains ![]() $\{\Omega _{j}\}_{j=1}^{\infty }$ such that
$\{\Omega _{j}\}_{j=1}^{\infty }$ such that ![]() $\Omega _1\neq \emptyset$,
$\Omega _1\neq \emptyset$, ![]() $\Omega _j \Subset \Omega _{j+1}$ and
$\Omega _j \Subset \Omega _{j+1}$ and ![]() $\bigcup _{j=1}^{\infty }\Omega _j=\Omega$.
$\bigcup _{j=1}^{\infty }\Omega _j=\Omega$.
2.3 Criticality theory for  $Q_{p,A,V}$
$Q_{p,A,V}$
Let ![]() $1< p<\infty$, and consider the operator
$1< p<\infty$, and consider the operator
defined on a domain ![]() $\Omega \subset \mathbb {R}^{n},\, n\geq 2$, where
$\Omega \subset \mathbb {R}^{n},\, n\geq 2$, where ![]() $\Delta _{p,A}:=\mathrm {div}(| \nabla u|_A^{p-2} A \nabla u)$ and
$\Delta _{p,A}:=\mathrm {div}(| \nabla u|_A^{p-2} A \nabla u)$ and ![]() $\mathcal {I}_p(u):=|u|^{p-2}u$. Unless otherwise stated, we always assume that the matrix
$\mathcal {I}_p(u):=|u|^{p-2}u$. Unless otherwise stated, we always assume that the matrix ![]() $A$ and the potential function
$A$ and the potential function ![]() $V$ satisfy the following regularity assumptions:
$V$ satisfy the following regularity assumptions:
Assumptions 2.8
•
 $A(x)=(a^{ij}(x))_{i,j=1}^{n}\in C^{\alpha }_{{\textrm {loc}}}(\Omega,\,\mathbb {R}^{n^{2}})$ is a symmetric positive definite matrix which is locally uniformly elliptic, that is, for any compact
$A(x)=(a^{ij}(x))_{i,j=1}^{n}\in C^{\alpha }_{{\textrm {loc}}}(\Omega,\,\mathbb {R}^{n^{2}})$ is a symmetric positive definite matrix which is locally uniformly elliptic, that is, for any compact  $K\Subset \Omega$ there exists
$K\Subset \Omega$ there exists  $\Theta _K>0$ such that
$\Theta _K>0$ such that
 \[ \Theta_K^{{-}1}\sum_{i=1}^{n}\xi_i^{2}\leq\sum_{i,j=1}^{n} a^{ij}(x)\xi_i\xi_j\leq \Theta_K\sum_{i=1}^{n}\xi_i^{2} \quad \forall \xi\in \mathbb{R}^{n} \text{ and } \forall x\in K. \]
\[ \Theta_K^{{-}1}\sum_{i=1}^{n}\xi_i^{2}\leq\sum_{i,j=1}^{n} a^{ij}(x)\xi_i\xi_j\leq \Theta_K\sum_{i=1}^{n}\xi_i^{2} \quad \forall \xi\in \mathbb{R}^{n} \text{ and } \forall x\in K. \]•
 $V\in M^{q}_{{\textrm {loc}}}(p;\Omega )$ is a real valued function.
$V\in M^{q}_{{\textrm {loc}}}(p;\Omega )$ is a real valued function.
The associated energy functional for the operator ![]() $Q_{p,A,V}$ in
$Q_{p,A,V}$ in ![]() $\Omega$ is defined by
$\Omega$ is defined by
Definition 2.9 We say that ![]() $u\in W^{1,p}_{{\textrm {loc}}}(\Omega )$ is a (weak) solution (resp. supersolution) of
$u\in W^{1,p}_{{\textrm {loc}}}(\Omega )$ is a (weak) solution (resp. supersolution) of ![]() $Q_{p,A,V}(u) =0$ in
$Q_{p,A,V}(u) =0$ in ![]() $\Omega$ if for any
$\Omega$ if for any ![]() $\phi \in C_0^{\infty }(\Omega )$ (resp.
$\phi \in C_0^{\infty }(\Omega )$ (resp. ![]() $0\leq \phi \in C_0^{\infty }(\Omega )$)
$0\leq \phi \in C_0^{\infty }(\Omega )$)
It should be noted that the above definition makes sense due to the following Morrey–Adams theorem (see, e.g., [Reference Pinchover and Psaradakis19, theorem 2.4] and references therein).
Theorem 2.10 Morrey–Adams theorem
Let ![]() $\omega \Subset \mathbb {R}^{n}$ and
$\omega \Subset \mathbb {R}^{n}$ and ![]() $V\in M^{q}(p;\omega )$.
$V\in M^{q}(p;\omega )$.
(i) There exists a constant
 $C=C(n,\,p,\,q)>0$ such that for any
$C=C(n,\,p,\,q)>0$ such that for any  $\delta >0$
$\delta >0$
 \[ \int_{\omega}|V||u|^{p} \,\mathrm{d}x \leq \delta \|\nabla u\|^{p}_{L^{p}(\omega,\mathbb{R}^{n})}+\ \frac{C}{\delta^{n/(pq-n)}}\|V\|^{pq/(pq-n)}_{M^{q}(p;\omega)}\|u\|^{p}_{L^{p}(\omega)} \quad \forall u\in W^{1,p}_{0}(\omega). \]
\[ \int_{\omega}|V||u|^{p} \,\mathrm{d}x \leq \delta \|\nabla u\|^{p}_{L^{p}(\omega,\mathbb{R}^{n})}+\ \frac{C}{\delta^{n/(pq-n)}}\|V\|^{pq/(pq-n)}_{M^{q}(p;\omega)}\|u\|^{p}_{L^{p}(\omega)} \quad \forall u\in W^{1,p}_{0}(\omega). \](ii) For any
 $\omega '\Subset \omega$ with Lipschitz boundary, there exists a positive constant
$\omega '\Subset \omega$ with Lipschitz boundary, there exists a positive constant  $C= C(n,\,p,\,q,\,\omega ',\,\omega,\,\delta,\,\|V\|_{M^{q}(p;\omega )})$ and
$C= C(n,\,p,\,q,\,\omega ',\,\omega,\,\delta,\,\|V\|_{M^{q}(p;\omega )})$ and  $\delta _0$ such that for
$\delta _0$ such that for  $0<\delta \leq \delta _0$
$0<\delta \leq \delta _0$
 \[ \int_{\omega'}|V||u|^{p} \,\mathrm{d}x \leq \delta \|\nabla u\|^{p}_{L^{p}(\omega',\mathbb{R}^{n})} +C\|u\|^{p}_{L^{p}(\omega')} \quad \forall u\in W^{1,p}(\omega'). \]
\[ \int_{\omega'}|V||u|^{p} \,\mathrm{d}x \leq \delta \|\nabla u\|^{p}_{L^{p}(\omega',\mathbb{R}^{n})} +C\|u\|^{p}_{L^{p}(\omega')} \quad \forall u\in W^{1,p}(\omega'). \]
We denote the set of all positive solutions (resp., supersolutions) of ![]() $Q_{p,A,V}(u)=0$ in
$Q_{p,A,V}(u)=0$ in ![]() $\Omega$ by
$\Omega$ by ![]() $\mathcal {C}^{Q_{p,A,V}}(\Omega )$ (resp.,
$\mathcal {C}^{Q_{p,A,V}}(\Omega )$ (resp., ![]() $\mathcal {K}^{Q_{p,A,V}}(\Omega )).$ We say that the operator
$\mathcal {K}^{Q_{p,A,V}}(\Omega )).$ We say that the operator ![]() $Q_{p,A,V}$ is nonnegative (in short
$Q_{p,A,V}$ is nonnegative (in short ![]() $Q_{p,A,V} \geq 0$) in
$Q_{p,A,V} \geq 0$) in ![]() $\Omega$ if
$\Omega$ if ![]() $\mathcal {C}^{Q_{p,A,V}}\neq \emptyset$.
$\mathcal {C}^{Q_{p,A,V}}\neq \emptyset$.
Remark 2.11 A weak (super)solution of the equation ![]() $-\Delta _{p,A}(u)=0$ in
$-\Delta _{p,A}(u)=0$ in ![]() $\Omega$ is said to be a
$\Omega$ is said to be a ![]() $(p,\,A)$-(super)harmonic function in
$(p,\,A)$-(super)harmonic function in ![]() $\Omega$.
$\Omega$.
It is well known that under assumptions 2.8 any positive solution of the equation ![]() $Q_{p,A,V}(u)=0$ in
$Q_{p,A,V}(u)=0$ in ![]() $\Omega$ belongs to
$\Omega$ belongs to ![]() $C^{1,\alpha }(\Omega )$ (see, e.g. [Reference Pinchover and Psaradakis19, remark 1.1]). Furthermore, the following Harnack convergence principle holds true.
$C^{1,\alpha }(\Omega )$ (see, e.g. [Reference Pinchover and Psaradakis19, remark 1.1]). Furthermore, the following Harnack convergence principle holds true.
Proposition 2.12 Harnack convergence principle [Reference Giri and Pinchover13, proposition 2.7]
Let ![]() $\{\Omega _{k}\}_{k\in \mathbb {N}}$ be an exhaustion of
$\{\Omega _{k}\}_{k\in \mathbb {N}}$ be an exhaustion of ![]() $\Omega$. Assume that
$\Omega$. Assume that ![]() $\{A_k\}_{k\in \mathbb {N}}$ is a sequence of symmetric and locally uniformly positive definite matrices such that the local ellipticity constants do not depend on
$\{A_k\}_{k\in \mathbb {N}}$ is a sequence of symmetric and locally uniformly positive definite matrices such that the local ellipticity constants do not depend on ![]() $k,$ and
$k,$ and ![]() $\{A_k\}_{k\in \mathbb {N}}\subset L^{\infty }_{{\textrm {loc}}}(\Omega _k,\,\mathbb {R}^{n^{2}})$ converges weakly in
$\{A_k\}_{k\in \mathbb {N}}\subset L^{\infty }_{{\textrm {loc}}}(\Omega _k,\,\mathbb {R}^{n^{2}})$ converges weakly in ![]() $L^{\infty }_{{\textrm {loc}}}(\Omega,\,\mathbb {R}^{n^{2}})$ to a matrix
$L^{\infty }_{{\textrm {loc}}}(\Omega,\,\mathbb {R}^{n^{2}})$ to a matrix ![]() $A\in L^{\infty }_{{\textrm {loc}}}(\Omega,\,\mathbb {R}^{n^{2}})$. Assume further that
$A\in L^{\infty }_{{\textrm {loc}}}(\Omega,\,\mathbb {R}^{n^{2}})$. Assume further that ![]() $\{V_k\}_{k\in \mathbb {N}}\subset M^{q}_{{\textrm {loc}}}(p;\Omega _k)$ converges weakly in
$\{V_k\}_{k\in \mathbb {N}}\subset M^{q}_{{\textrm {loc}}}(p;\Omega _k)$ converges weakly in ![]() $M^{q}_{{\textrm {loc}}}(p;\Omega )$ to
$M^{q}_{{\textrm {loc}}}(p;\Omega )$ to ![]() $V\in M^{q}_{{\textrm {loc}}}(p;\Omega )$. For each
$V\in M^{q}_{{\textrm {loc}}}(p;\Omega )$. For each ![]() $k,$ let
$k,$ let ![]() $v_k$ be a positive solution of the equation
$v_k$ be a positive solution of the equation ![]() $Q_{p,A_k,V_k}(u)=0$ in
$Q_{p,A_k,V_k}(u)=0$ in ![]() $\Omega _k$ such that
$\Omega _k$ such that ![]() $v_k(x_0)=1,$ where
$v_k(x_0)=1,$ where ![]() $x_0$ is a fixed reference point in
$x_0$ is a fixed reference point in ![]() $\Omega _1$. Then there exists
$\Omega _1$. Then there exists ![]() $0<\beta <1$ such that, up to a subsequence,
$0<\beta <1$ such that, up to a subsequence, ![]() $\{v_k\}_{k\in \mathbb {N}}$ converges weakly in
$\{v_k\}_{k\in \mathbb {N}}$ converges weakly in ![]() $W^{1,p}_{{\textrm {loc}}}(\Omega )$ and in
$W^{1,p}_{{\textrm {loc}}}(\Omega )$ and in ![]() $C_{{\textrm {loc}}}^{\beta }(\Omega )$ to a positive weak solution
$C_{{\textrm {loc}}}^{\beta }(\Omega )$ to a positive weak solution ![]() $v$ of the equation
$v$ of the equation ![]() $Q_{p,A,V}(u)=0$ in
$Q_{p,A,V}(u)=0$ in ![]() $\Omega$.
$\Omega$.
Definition 2.13 Let ![]() $\Omega \subset \mathbb {R}^{n}$ be a bounded Lipschitz domain. A principal eigenvalue of
$\Omega \subset \mathbb {R}^{n}$ be a bounded Lipschitz domain. A principal eigenvalue of ![]() $Q_{p,A,V}$ in
$Q_{p,A,V}$ in ![]() $\Omega$ is an eigenvalue
$\Omega$ is an eigenvalue ![]() $\lambda$ of the problem
$\lambda$ of the problem
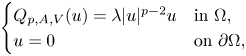 \[ \begin{cases} Q_{p,A,V}(u)=\lambda |u|^{p-2}u & \text{in } \Omega, \\ u=0 & \text{on } \partial \Omega, \end{cases} \]
\[ \begin{cases} Q_{p,A,V}(u)=\lambda |u|^{p-2}u & \text{in } \Omega, \\ u=0 & \text{on } \partial \Omega, \end{cases} \]
with a nonzero nonnegative ![]() $u$ which is called a principal eigenfunction.
$u$ which is called a principal eigenfunction.
Proposition 2.14 [Reference Pinchover and Psaradakis19, theorem 3.9]
Let ![]() $\Omega \subset \mathbb {R}^{n}$ be a bounded Lipschitz domain, and assume that
$\Omega \subset \mathbb {R}^{n}$ be a bounded Lipschitz domain, and assume that ![]() $A$ is a uniformly elliptic, bounded matrix in
$A$ is a uniformly elliptic, bounded matrix in ![]() $\Omega,$ and
$\Omega,$ and ![]() $V\in M^{q}(p;\Omega )$. Then, the operator
$V\in M^{q}(p;\Omega )$. Then, the operator ![]() $Q_{p,A,V}$ admits a unique principal eigenvalue
$Q_{p,A,V}$ admits a unique principal eigenvalue ![]() $\lambda _1(\Omega )$. Moreover,
$\lambda _1(\Omega )$. Moreover, ![]() $\lambda _1$ is simple and its principal eigenfunction is the minimizer of the Rayleigh–Ritz variational problem
$\lambda _1$ is simple and its principal eigenfunction is the minimizer of the Rayleigh–Ritz variational problem
 \[ \lambda_1(\Omega)=\min\limits_{u \in W^{1,p}_{0}\setminus \{0\}}\dfrac{\mathcal{Q}^{\Omega}_{p,A,V}(u)}{\|u\|^{p}_{L^{p}(\Omega)}}. \]
\[ \lambda_1(\Omega)=\min\limits_{u \in W^{1,p}_{0}\setminus \{0\}}\dfrac{\mathcal{Q}^{\Omega}_{p,A,V}(u)}{\|u\|^{p}_{L^{p}(\Omega)}}. \] The following well-known Allegretto–Piepenbrink theorem (in short, the AP theorem) connects between the nonnegativity of ![]() $Q_{p,A,V}$ and the nonnegativity of its associated energy functional
$Q_{p,A,V}$ and the nonnegativity of its associated energy functional ![]() $\mathcal {Q}^{\Omega }_{p,A,V}$ [Reference Pinchover and Psaradakis19, theorem 4.3].
$\mathcal {Q}^{\Omega }_{p,A,V}$ [Reference Pinchover and Psaradakis19, theorem 4.3].
Theorem 2.15 AP theorem
The following assertions are equivalent.
(i)
 $\mathcal {Q}_{p,A,V}^{\Omega }(\phi ) \geq 0$ for all
$\mathcal {Q}_{p,A,V}^{\Omega }(\phi ) \geq 0$ for all  $\phi \in {C_0^{\infty }(\Omega )}.$
$\phi \in {C_0^{\infty }(\Omega )}.$(ii)
 $\mathcal {C}^{Q_{p,A,V}}(\Omega )\neq \emptyset.$
$\mathcal {C}^{Q_{p,A,V}}(\Omega )\neq \emptyset.$(iii)
 $\mathcal {K}^{Q_{p,A,V}}(\Omega )\neq \emptyset.$
$\mathcal {K}^{Q_{p,A,V}}(\Omega )\neq \emptyset.$
Definition 2.16 Assume that ![]() $Q_{p,A,V}\geq 0$ in
$Q_{p,A,V}\geq 0$ in ![]() $\Omega.$ We say that
$\Omega.$ We say that ![]() $Q_{p,A,V}$ is subcritical in
$Q_{p,A,V}$ is subcritical in ![]() $\Omega$ if there exists
$\Omega$ if there exists ![]() $0\lneqq W\in M^{q}_{{\textrm {loc}}}(p;\Omega )$ such that
$0\lneqq W\in M^{q}_{{\textrm {loc}}}(p;\Omega )$ such that ![]() $Q_{p,A,V-W}\geq 0$ in
$Q_{p,A,V-W}\geq 0$ in ![]() $\Omega$. We say that
$\Omega$. We say that ![]() $Q_{p,A,V}$ is critical in
$Q_{p,A,V}$ is critical in ![]() $\Omega$ if for all
$\Omega$ if for all ![]() $0\lneqq W\in M^{q}_{{\textrm {loc}}}(p;\Omega )$ the equation
$0\lneqq W\in M^{q}_{{\textrm {loc}}}(p;\Omega )$ the equation ![]() $Q_{p,A,V-W}(u)=0$ does not admit a positive solution in
$Q_{p,A,V-W}(u)=0$ does not admit a positive solution in ![]() $\Omega.$
$\Omega.$
Definition 2.17 Let ![]() $\omega$ be a bounded Lipschitz domain. We say that
$\omega$ be a bounded Lipschitz domain. We say that ![]() $Q_{p,A,V}$ satisfies the (generalized) weak maximum principle in
$Q_{p,A,V}$ satisfies the (generalized) weak maximum principle in ![]() $\omega$ if for any
$\omega$ if for any ![]() $u\in W^{1,p}(\omega )$ satisfying
$u\in W^{1,p}(\omega )$ satisfying ![]() $Q_{p,A,V}(u)\geq 0$ in
$Q_{p,A,V}(u)\geq 0$ in ![]() $\omega$ and
$\omega$ and ![]() $u\geq 0$ on
$u\geq 0$ on ![]() $\partial \omega$, we have
$\partial \omega$, we have ![]() $u\geq 0$ in
$u\geq 0$ in ![]() $\omega$.
$\omega$.
We say that ![]() $Q_{p,A,V}$ satisfies the strong maximum principle in
$Q_{p,A,V}$ satisfies the strong maximum principle in ![]() $\omega$ if for any
$\omega$ if for any ![]() $u\in W^{1,p}(\omega )$ satisfying
$u\in W^{1,p}(\omega )$ satisfying ![]() $Q_{p,A,V}(u)\geq 0$ in
$Q_{p,A,V}(u)\geq 0$ in ![]() $\omega$ and
$\omega$ and ![]() $u\geq 0$ on
$u\geq 0$ on ![]() $\partial \omega$, either
$\partial \omega$, either ![]() $u = 0$, or
$u = 0$, or ![]() $u>0$ in
$u>0$ in ![]() $\omega$.
$\omega$.
Lemma 2.18 [Reference Pinchover and Psaradakis19, theorem 3.10]
Let ![]() $\Omega$ be a bounded Lipschitz domain, and assume that
$\Omega$ be a bounded Lipschitz domain, and assume that ![]() $A$ is a uniformly elliptic, bounded matrix in
$A$ is a uniformly elliptic, bounded matrix in ![]() $\Omega,$ and
$\Omega,$ and ![]() $V\in M^{q}(p;\Omega )$. Then the following assertions are equivalent.
$V\in M^{q}(p;\Omega )$. Then the following assertions are equivalent.
(i)
 $Q_{p,A,V}$ satisfies the (generalized) weak maximum principle in
$Q_{p,A,V}$ satisfies the (generalized) weak maximum principle in  $\Omega$.
$\Omega$.(ii)
 $Q_{p,A,V}$ satisfies the strong maximum principle in
$Q_{p,A,V}$ satisfies the strong maximum principle in  $\Omega$.
$\Omega$.(iii) The equation
 $Q_{p,A,V}(u)=0$ admits a positive supersolution in
$Q_{p,A,V}(u)=0$ admits a positive supersolution in  $W^{1,p}_{0}(\Omega )$ which is not a solution.
$W^{1,p}_{0}(\Omega )$ which is not a solution.(iv) The equation
 $Q_{p,A,V}(u)=0$ admits a positive supersolution in
$Q_{p,A,V}(u)=0$ admits a positive supersolution in  $W^{1,p}(\Omega )$ which is not a solution.
$W^{1,p}(\Omega )$ which is not a solution.(v)
 $\lambda _1(\Omega )>0$.
$\lambda _1(\Omega )>0$.(vi) For any
 $0\leq g\in L^{p'}(\Omega ),$ there exists a unique nonnegative solution in
$0\leq g\in L^{p'}(\Omega ),$ there exists a unique nonnegative solution in  $W^{1,p}_{0}(\Omega )$ of
$W^{1,p}_{0}(\Omega )$ of  $Q_{p,A,V}(u)=g$.
$Q_{p,A,V}(u)=g$.
Corollary 2.19 If there exists a weak positive (super)solution of ![]() $Q_{p,A,V} (u) =0$ in a domain
$Q_{p,A,V} (u) =0$ in a domain ![]() $\Omega \subset \mathbb {R}^{n},$ then
$\Omega \subset \mathbb {R}^{n},$ then ![]() $\lambda _1(\Omega ')>0$ for any bounded Lipschitz subdomain
$\lambda _1(\Omega ')>0$ for any bounded Lipschitz subdomain ![]() $\Omega '\Subset \Omega$.
$\Omega '\Subset \Omega$.
Definition 2.20 Let ![]() $K_0$ be a compact subset of
$K_0$ be a compact subset of ![]() $\Omega$. A positive solution
$\Omega$. A positive solution ![]() $u$ of
$u$ of ![]() $Q_{p,A,V}(u)=0$ in
$Q_{p,A,V}(u)=0$ in ![]() $\Omega \setminus K_0$ is said to be a positive solution of minimal growth in a neighbourhood of infinity in
$\Omega \setminus K_0$ is said to be a positive solution of minimal growth in a neighbourhood of infinity in ![]() $\Omega$, and denoted by
$\Omega$, and denoted by ![]() $u\in \mathcal {MG}_{A,V,\Omega ;K_0}$, if for any smooth compact subset
$u\in \mathcal {MG}_{A,V,\Omega ;K_0}$, if for any smooth compact subset ![]() $K$ of
$K$ of ![]() $\Omega$ with
$\Omega$ with ![]() $K_0 \Subset \mathrm {int} (K)$, and any positive supersolution
$K_0 \Subset \mathrm {int} (K)$, and any positive supersolution ![]() $v \in C(\Omega \setminus K)$ of
$v \in C(\Omega \setminus K)$ of ![]() $Q_{p,A,V}(w)=0$ in
$Q_{p,A,V}(w)=0$ in ![]() $\Omega \setminus K$, we have
$\Omega \setminus K$, we have
If ![]() $u\in \mathcal {MG}_{A,V,\Omega ; \emptyset },$ then
$u\in \mathcal {MG}_{A,V,\Omega ; \emptyset },$ then ![]() $u$ is called an Agmon ground state of
$u$ is called an Agmon ground state of ![]() $Q_{p,A,V}$ in
$Q_{p,A,V}$ in ![]() $\Omega.$
$\Omega.$
Lemma 2.21 [Reference Giri and Pinchover13, proposition 3.17]
Let ![]() $V\in M^{q}_{{\textrm {loc}}}(p;\Omega ),$ and suppose that
$V\in M^{q}_{{\textrm {loc}}}(p;\Omega ),$ and suppose that ![]() $Q_{p,A,V} \geq 0$ in
$Q_{p,A,V} \geq 0$ in ![]() $\Omega.$ Then for any
$\Omega.$ Then for any ![]() $x_0\in \Omega$ the equation
$x_0\in \Omega$ the equation ![]() $Q_{p,A,V}(w)=0$ admits a unique (up to a multiplicative constant) solution
$Q_{p,A,V}(w)=0$ admits a unique (up to a multiplicative constant) solution ![]() $u\in \mathcal {MG}_{A,V,\Omega ; \{x_0\}}.$
$u\in \mathcal {MG}_{A,V,\Omega ; \{x_0\}}.$
Definition 2.22 A function ![]() $u\in \mathcal {MG}_{A,V,\Omega ; \{x_0\}}$ having a nonremovable singularity at
$u\in \mathcal {MG}_{A,V,\Omega ; \{x_0\}}$ having a nonremovable singularity at ![]() $x_0$ is called a minimal positive Green function of
$x_0$ is called a minimal positive Green function of ![]() $Q_{p,A,V}$ in
$Q_{p,A,V}$ in ![]() $\Omega$ with singularity at
$\Omega$ with singularity at ![]() $x_0.$ We denote such a function by
$x_0.$ We denote such a function by ![]() $G^{\Omega }_{Q_{p,A,V}}(x,\,x_0).$
$G^{\Omega }_{Q_{p,A,V}}(x,\,x_0).$
Lemma 2.23 [Reference Pinchover and Psaradakis19, theorem 5.9]
Suppose that ![]() $Q_{p,A,V} \geq 0$ in
$Q_{p,A,V} \geq 0$ in ![]() $\Omega$. Then
$\Omega$. Then ![]() $Q_{p,A,V}$ is critical in
$Q_{p,A,V}$ is critical in ![]() $\Omega$ if and only if the equation
$\Omega$ if and only if the equation ![]() $Q_{p,A,V}=0$ admits a ground state in
$Q_{p,A,V}=0$ admits a ground state in ![]() $\Omega$.
$\Omega$.
Definition 2.24 A sequence ![]() $\{\phi _k \}_{k\in \mathbb {N}}\subset C_0^{\infty }(\Omega )$ is called a null-sequence with respect to a nonnegative operator
$\{\phi _k \}_{k\in \mathbb {N}}\subset C_0^{\infty }(\Omega )$ is called a null-sequence with respect to a nonnegative operator ![]() $Q_{p,A,V}$ in
$Q_{p,A,V}$ in ![]() $\Omega$ if
$\Omega$ if
(i)
 $\phi _k \geq 0$ for all
$\phi _k \geq 0$ for all  $k\in \mathbb {N},$
$k\in \mathbb {N},$(ii) there exists a fixed open set
 $B\Subset \Omega$ such that
$B\Subset \Omega$ such that  $\| \phi _k\|_{L^{p}(B)}\asymp 1$ for all
$\| \phi _k\|_{L^{p}(B)}\asymp 1$ for all  $k\in N,$
$k\in N,$(iii)
 $\lim \limits _{k\to \infty }\mathcal {Q}^{\Omega }_{p,A,V}(\phi _k)=0.$
$\lim \limits _{k\to \infty }\mathcal {Q}^{\Omega }_{p,A,V}(\phi _k)=0.$
Lemma 2.25 [Reference Pinchover and Psaradakis19, theorem 4.15]
A nonnegative operator ![]() $Q_{p,A,V}$ is critical in
$Q_{p,A,V}$ is critical in ![]() $\Omega$ if and only if
$\Omega$ if and only if ![]() $Q_{p,A,V}$ admits a null-sequence in
$Q_{p,A,V}$ admits a null-sequence in ![]() $\Omega.$
$\Omega.$
The next lemma shows that the energy functional ![]() $\mathcal {Q}^{\Omega }_{p,A,V}$ is equivalent to a simplified energy that does not explicitly depend on
$\mathcal {Q}^{\Omega }_{p,A,V}$ is equivalent to a simplified energy that does not explicitly depend on ![]() $V$ and contains only nonnegative terms.
$V$ and contains only nonnegative terms.
Lemma 2.26 [Reference Pinchover and Regev20, lemma 3.4]
Let ![]() $v\in \mathcal {C}^{Q_{p,A,V}}(\Omega )$. Then, for any
$v\in \mathcal {C}^{Q_{p,A,V}}(\Omega )$. Then, for any ![]() $0\leq u\in W^{1,p}_{{\textrm {loc}}}(\Omega )$ having compact support in
$0\leq u\in W^{1,p}_{{\textrm {loc}}}(\Omega )$ having compact support in ![]() $\Omega,$ and such that
$\Omega,$ and such that ![]() $w:=u/v\in L^{\infty }_{{\textrm {loc}}}(\Omega ),$ we have
$w:=u/v\in L^{\infty }_{{\textrm {loc}}}(\Omega ),$ we have
Remark 2.27 Lemma 2.26 is proved in [Reference Pinchover and Regev20] for the case ![]() $V\in L^{\infty }_{{\textrm {loc}}}(\Omega )$. However, the proof is purely algebraic and therefore, holds for
$V\in L^{\infty }_{{\textrm {loc}}}(\Omega )$. However, the proof is purely algebraic and therefore, holds for ![]() $V\in M^{q}_{{\textrm {loc}}}(p;\Omega )$ as well.
$V\in M^{q}_{{\textrm {loc}}}(p;\Omega )$ as well.
As a corollary of (2.2) and Hölder's inequality we obtain the following.
Corollary 2.28 Let ![]() $v\in \mathcal {C}^{Q_{p,A,V}}(\Omega )\cap C^{1,\alpha }_{{\textrm {loc}}}(\Omega )$ and let
$v\in \mathcal {C}^{Q_{p,A,V}}(\Omega )\cap C^{1,\alpha }_{{\textrm {loc}}}(\Omega )$ and let ![]() $X(w):=\int _{\Omega }v^{p}|\nabla w|_A^{p} \,\mathrm {d}x$ and
$X(w):=\int _{\Omega }v^{p}|\nabla w|_A^{p} \,\mathrm {d}x$ and ![]() $Y(w):=\int _{\Omega }|w|^{p}|\nabla v|_A^{p} \,\mathrm {d}x$. Then, for any continuous function
$Y(w):=\int _{\Omega }|w|^{p}|\nabla v|_A^{p} \,\mathrm {d}x$. Then, for any continuous function ![]() $w\in W^{1,p}(\Omega )$ having compact support in
$w\in W^{1,p}(\Omega )$ having compact support in ![]() $\Omega,$ the following assertions hold true.
$\Omega,$ the following assertions hold true.
(i)
 $\mathcal {Q}^{\Omega }_{p,A,V}(vw)\asymp \mathcal {Q}^{\Omega }_{\mathrm {sim},\,p,\,A,\,V}(w)$.
$\mathcal {Q}^{\Omega }_{p,A,V}(vw)\asymp \mathcal {Q}^{\Omega }_{\mathrm {sim},\,p,\,A,\,V}(w)$.(ii)
 $\mathcal {Q}^{\Omega }_{\mathrm {sim},\,p,\,A,\,V}(w) \leq \begin {cases} CX(w) & 1< p\leq 2,\, \\ C [ X(w)+X(w)^{2/p}Y(w)^{\frac {p-2}{p}}] & p>2. \end {cases}$
$\mathcal {Q}^{\Omega }_{\mathrm {sim},\,p,\,A,\,V}(w) \leq \begin {cases} CX(w) & 1< p\leq 2,\, \\ C [ X(w)+X(w)^{2/p}Y(w)^{\frac {p-2}{p}}] & p>2. \end {cases}$
2.4 Optimal Hardy-weights
Let ![]() $\overline {\infty }$ denote the ideal point in the one-point compactification of
$\overline {\infty }$ denote the ideal point in the one-point compactification of ![]() $\Omega$. Let us define the notion of an optimal Hardy-weight for the operator
$\Omega$. Let us define the notion of an optimal Hardy-weight for the operator ![]() $Q_{p,A,V}$.
$Q_{p,A,V}$.
Definition 2.29 [Reference Devyver and Pinchover9]
Suppose that ![]() $Q_{p,A,V}$ is subcritical in
$Q_{p,A,V}$ is subcritical in ![]() $\Omega$. We say that
$\Omega$. We say that ![]() $0\lneqq W$ is an optimal Hardy-weight of
$0\lneqq W$ is an optimal Hardy-weight of ![]() $Q_{p,A,V}$ in
$Q_{p,A,V}$ in ![]() $\Omega$ if the following two assertions are satisfied:
$\Omega$ if the following two assertions are satisfied:
(i) Criticality:
 $Q_{p,A,V-W}$ is critical in
$Q_{p,A,V-W}$ is critical in  $\Omega.$
$\Omega.$(ii) Null-criticality with respect to
 $W$:
$W$:  $\int _\Omega |\psi |^{p} W\,\mathrm {d}x=\infty$, where
$\int _\Omega |\psi |^{p} W\,\mathrm {d}x=\infty$, where  $\psi$ is the (Agmon) ground state of
$\psi$ is the (Agmon) ground state of  $Q_{p,A,V-W}$ in
$Q_{p,A,V-W}$ in  $\Omega.$
$\Omega.$
Remark 2.30 Let us discuss definition 2.29. Suppose that ![]() $Q_{p,A,V}$ is subcritical in a domain
$Q_{p,A,V}$ is subcritical in a domain ![]() $\Omega$ containing
$\Omega$ containing ![]() $x_0$, and let
$x_0$, and let ![]() $x_0\in K\Subset \Omega$. Then, for any
$x_0\in K\Subset \Omega$. Then, for any ![]() $0\lneqq W \in C_0^{\infty }(\Omega )$ there exists
$0\lneqq W \in C_0^{\infty }(\Omega )$ there exists ![]() $\tau >0$ such that
$\tau >0$ such that ![]() $Q_{p,A,V-\tau W}$ is critical in
$Q_{p,A,V-\tau W}$ is critical in ![]() $\Omega$ (see, e.g. [Reference Pinchover and Tintarev21, proposition 4.4] and [Reference Pinchover and Psaradakis19]). On the other hand, the ground state of
$\Omega$ (see, e.g. [Reference Pinchover and Tintarev21, proposition 4.4] and [Reference Pinchover and Psaradakis19]). On the other hand, the ground state of ![]() $Q_{p,A,V-\tau W}$,
$Q_{p,A,V-\tau W}$, ![]() $\phi$, satisfies
$\phi$, satisfies
Therefore, there are infinity many weight functions ![]() $0\lneqq W\in C_0^{\infty }(\Omega )$ such that
$0\lneqq W\in C_0^{\infty }(\Omega )$ such that ![]() $Q_{p,A,V -W}$ is critical in
$Q_{p,A,V -W}$ is critical in ![]() $\Omega$. Obviously, for such a weight
$\Omega$. Obviously, for such a weight ![]() $W$, the operator
$W$, the operator ![]() $Q_{p,A,V -W}$ is not null-critical with respect to
$Q_{p,A,V -W}$ is not null-critical with respect to ![]() $W$.
$W$.
Definition 2.31 We say that a Hardy-weight ![]() $W$ is optimal at infinity in
$W$ is optimal at infinity in ![]() $\Omega$ if for any
$\Omega$ if for any ![]() $K\Subset \Omega$, we have
$K\Subset \Omega$, we have
Remark 2.32 The definition of an optimal Hardy-weight in [Reference Devyver, Fraas and Pinchover8] includes the requirement that ![]() $W$ should be optimal at infinity. But, it is proved in [Reference Kovařík and Pinchover15] that if
$W$ should be optimal at infinity. But, it is proved in [Reference Kovařík and Pinchover15] that if ![]() $Q - W$ is null-critical with respect to
$Q - W$ is null-critical with respect to ![]() $W$ in
$W$ in ![]() $\Omega$, then
$\Omega$, then ![]() $Q-W$ is optimal at infinity. The same proof applies under the assumptions considered in the present paper, hence, in definition 2.29 we avoid the requirement of optimality at infinity.
$Q-W$ is optimal at infinity. The same proof applies under the assumptions considered in the present paper, hence, in definition 2.29 we avoid the requirement of optimality at infinity.
The following coarea formula is a direct consequence of [Reference Devyver and Pinchover9, proposition 3.1].
Lemma 2.33 Coarea formula
Let ![]() $\Omega$ be a domain in
$\Omega$ be a domain in ![]() $\mathbb {R}^{n},$
$\mathbb {R}^{n},$ ![]() $n\geq 2,$ and
$n\geq 2,$ and ![]() $G\in C^{1,\alpha }(\Omega )$ is a positive
$G\in C^{1,\alpha }(\Omega )$ is a positive ![]() $(p,\,A)$-harmonic function in
$(p,\,A)$-harmonic function in ![]() $\Omega ^{*} := \Omega \setminus \{0\}$. Assume that for any
$\Omega ^{*} := \Omega \setminus \{0\}$. Assume that for any ![]() $0< t_1< t_2 < \infty$, the set
$0< t_1< t_2 < \infty$, the set ![]() $\mathcal {A} := \{x \in \Omega ^{*} \mid t_1< G(x)< t_2\}$ is bounded. Let
$\mathcal {A} := \{x \in \Omega ^{*} \mid t_1< G(x)< t_2\}$ is bounded. Let ![]() $h\in {C^{2}(0,\,\infty )}$ be a positive function satisfying
$h\in {C^{2}(0,\,\infty )}$ be a positive function satisfying ![]() $h'(s)>0$ for all
$h'(s)>0$ for all ![]() $s>0$, and denote
$s>0$, and denote ![]() $v:=h(G)$. Then there exists
$v:=h(G)$. Then there exists ![]() $C>0$ such that for any locally bounded real measurable function
$C>0$ such that for any locally bounded real measurable function ![]() $f$ such that
$f$ such that ![]() $f(v)$ has a compact support in
$f(v)$ has a compact support in ![]() $\Omega ^{*},$ we have
$\Omega ^{*},$ we have
 \begin{equation} \int_{\Omega^{*}}f(v)|\nabla v|_A^{p} \mathrm{d}x=C\int_{h(\inf_{\Omega*} G)}^{h(\sup_{\Omega*} G)} \frac{f(\tau)}{((h^{{-}1})'(\tau))^{p-1}} \,\mathrm{d}\tau. \end{equation}
\begin{equation} \int_{\Omega^{*}}f(v)|\nabla v|_A^{p} \mathrm{d}x=C\int_{h(\inf_{\Omega*} G)}^{h(\sup_{\Omega*} G)} \frac{f(\tau)}{((h^{{-}1})'(\tau))^{p-1}} \,\mathrm{d}\tau. \end{equation}Proof. Since ![]() $G\in C^{1,\alpha }(\Omega ^{*})$ and
$G\in C^{1,\alpha }(\Omega ^{*})$ and ![]() $1< p$, then
$1< p$, then ![]() $\frac {|\nabla G|_A^{p}}{|\nabla G|}\in L^{1}_{{\textrm {loc}}}(\Omega ^{*})$ and we may use the (classical) coarea formula ([Reference Chen, Torres and Ziemer7, theorem 2.32]) to obtain for
$\frac {|\nabla G|_A^{p}}{|\nabla G|}\in L^{1}_{{\textrm {loc}}}(\Omega ^{*})$ and we may use the (classical) coarea formula ([Reference Chen, Torres and Ziemer7, theorem 2.32]) to obtain for ![]() $v=h(G)$
$v=h(G)$
 \begin{align} & \int_{\Omega^{*}}f(v)|\nabla v|_A^{p} \,\mathrm{d}x= \int_{\Omega^{*}}f(h(v))|h'(G)|^{p}\frac{|\nabla G|_A^{p}}{|\nabla G|}|\nabla G| \,\mathrm{d}x= \nonumber\\ & \int_{\mathbb{R}_+}f(h(t))h'(t)^{p}\int_{\{G=t\}}\frac{|\nabla G|_A^{p}}{|\nabla G|} \,\mathrm{d}\mathcal{H}^{n-1}. \end{align}
\begin{align} & \int_{\Omega^{*}}f(v)|\nabla v|_A^{p} \,\mathrm{d}x= \int_{\Omega^{*}}f(h(v))|h'(G)|^{p}\frac{|\nabla G|_A^{p}}{|\nabla G|}|\nabla G| \,\mathrm{d}x= \nonumber\\ & \int_{\mathbb{R}_+}f(h(t))h'(t)^{p}\int_{\{G=t\}}\frac{|\nabla G|_A^{p}}{|\nabla G|} \,\mathrm{d}\mathcal{H}^{n-1}. \end{align}
By (a generalized) Sard's theorem for ![]() $C^{1,\alpha }$ functions [Reference Bojarski, Hajlasz and Strzelecki5, theorem 1.2],
$C^{1,\alpha }$ functions [Reference Bojarski, Hajlasz and Strzelecki5, theorem 1.2],
The fact that ![]() $G\in C^{1,\alpha }$ and proposition 2.4 imply that (for a.e.
$G\in C^{1,\alpha }$ and proposition 2.4 imply that (for a.e. ![]() $t_1< t_2$) the set
$t_1< t_2$) the set ![]() $\mathcal {A}:=\{t_1< G< t_2\}$ has a finite perimeter. In particular,
$\mathcal {A}:=\{t_1< G< t_2\}$ has a finite perimeter. In particular, ![]() $\nabla G\neq 0$ and
$\nabla G\neq 0$ and ![]() $\vec {n}$ is well defined on
$\vec {n}$ is well defined on ![]() $\partial \mathcal {A}$,
$\partial \mathcal {A}$, ![]() $\mathcal {H}^{n-1}$-a.e.. Let
$\mathcal {H}^{n-1}$-a.e.. Let ![]() $\partial _+=\{x\in \overline {\mathcal {A}}: G(x)=t_2\}$ and
$\partial _+=\{x\in \overline {\mathcal {A}}: G(x)=t_2\}$ and ![]() $\partial _-=\{x\in \overline {\mathcal {A}}: G(x)=t_1\}$. The Gauss–Green theorem (lemma 2.5) implies that
$\partial _-=\{x\in \overline {\mathcal {A}}: G(x)=t_1\}$. The Gauss–Green theorem (lemma 2.5) implies that
 \begin{align*} 0 & ={-}\int_{\mathcal{A}}\!\!\mathrm{div}(|\nabla G|_A^{p-2}A\nabla G) \,\mathrm{d}x=\int_{\partial_{+}}+ \int_{\partial_{-}}\!|\nabla G|_A^{p-2}A\nabla G \cdot \vec{n} \,\mathrm{d}\mathcal{H}^{n-1}\\ & =\int_{\partial_{+}}|\nabla G|_A^{p-2}A\nabla G \cdot \frac{\nabla G}{|\nabla G|} \,\mathrm{d}\mathcal{H}^{n-1}- \int_{\partial_{-}}|\nabla G|_A^{p-2}A\nabla G \cdot \frac{\nabla G}{|\nabla G|} \,\mathrm{d}\mathcal{H}^{n-1}\\ & =\int_{\{G=t_2\}}\frac{|\nabla G|_A^{p}}{|\nabla G|} \,\mathrm{d}\mathcal{H}^{n-1}- \int_{\{G=t_1\}}\frac{|\nabla G|_A^{p}}{|\nabla G|} \,\mathrm{d}\mathcal{H}^{n-1}. \end{align*}
\begin{align*} 0 & ={-}\int_{\mathcal{A}}\!\!\mathrm{div}(|\nabla G|_A^{p-2}A\nabla G) \,\mathrm{d}x=\int_{\partial_{+}}+ \int_{\partial_{-}}\!|\nabla G|_A^{p-2}A\nabla G \cdot \vec{n} \,\mathrm{d}\mathcal{H}^{n-1}\\ & =\int_{\partial_{+}}|\nabla G|_A^{p-2}A\nabla G \cdot \frac{\nabla G}{|\nabla G|} \,\mathrm{d}\mathcal{H}^{n-1}- \int_{\partial_{-}}|\nabla G|_A^{p-2}A\nabla G \cdot \frac{\nabla G}{|\nabla G|} \,\mathrm{d}\mathcal{H}^{n-1}\\ & =\int_{\{G=t_2\}}\frac{|\nabla G|_A^{p}}{|\nabla G|} \,\mathrm{d}\mathcal{H}^{n-1}- \int_{\{G=t_1\}}\frac{|\nabla G|_A^{p}}{|\nabla G|} \,\mathrm{d}\mathcal{H}^{n-1}. \end{align*}
In particular, for any ![]() $t>0$,
$t>0$, ![]() $\int _{\{G=t\}}\frac {|\nabla G|_A^{p}}{|\nabla G|} \,\mathrm {d}\mathcal {H}^{n-1}=C$. By (2.4),
$\int _{\{G=t\}}\frac {|\nabla G|_A^{p}}{|\nabla G|} \,\mathrm {d}\mathcal {H}^{n-1}=C$. By (2.4),
The change of the variable ![]() $h(t)=\tau$ then implies (2.3).
$h(t)=\tau$ then implies (2.3).
The following theorem is proved in [Reference Devyver and Pinchover9] for the case ![]() $A=\mathbf {1}$. However, it can be easily checked that the validity of lemma 2.33 for a general matrix
$A=\mathbf {1}$. However, it can be easily checked that the validity of lemma 2.33 for a general matrix ![]() $A$ satisfying assumptions 2.8, gives rise to the following theorem.
$A$ satisfying assumptions 2.8, gives rise to the following theorem.
Theorem 2.34 [Reference Devyver and Pinchover9, theorem 1.5]
Let ![]() $\overline {\infty }$ denote the ideal point in the one point compactification of
$\overline {\infty }$ denote the ideal point in the one point compactification of ![]() $\Omega$. Suppose that
$\Omega$. Suppose that ![]() $-\Delta _{p,A}$ is subcritical in
$-\Delta _{p,A}$ is subcritical in ![]() $\Omega,$ and admits a positive
$\Omega,$ and admits a positive ![]() $(p,\,A)$-harmonic function
$(p,\,A)$-harmonic function ![]() $G(x)$ in
$G(x)$ in ![]() $\Omega ^{*}:=\Omega \setminus \{0\}$ satisfying one of the following conditions (2.5),(2.6):
$\Omega ^{*}:=\Omega \setminus \{0\}$ satisfying one of the following conditions (2.5),(2.6):
 \begin{align} p>n, \quad \lim\limits_{x\to 0}G(x)=\gamma\geq 0, \text{and } \lim\limits_{x\to \overline{\infty}}G(x)= \begin{cases} \infty & \text{if } \gamma=0,\\ 0 & \text{if } \gamma>0. \end{cases} \end{align}
\begin{align} p>n, \quad \lim\limits_{x\to 0}G(x)=\gamma\geq 0, \text{and } \lim\limits_{x\to \overline{\infty}}G(x)= \begin{cases} \infty & \text{if } \gamma=0,\\ 0 & \text{if } \gamma>0. \end{cases} \end{align}
Define a positive function ![]() $v$ and a nonnegative weight
$v$ and a nonnegative weight ![]() $W$ on
$W$ on ![]() $\Omega ^{*}$ as follows:
$\Omega ^{*}$ as follows:
(i) If either (2.5) is satisfied, or (2.6) is satisfied with
 $\gamma =0,$ then
$\gamma =0,$ then
 \[ v:=G^{(p-1)/p}, \text{ and } W:=\left( \frac{p-1}{p}\right)^{p}\left | \frac{\nabla G}{G}\right |_A^{p}. \]
\[ v:=G^{(p-1)/p}, \text{ and } W:=\left( \frac{p-1}{p}\right)^{p}\left | \frac{\nabla G}{G}\right |_A^{p}. \](ii) If (2.6) is satisfied with
 $\gamma >0,$ then
$\gamma >0,$ then  $v:= [G(\gamma -G)]^{(p-1)/p},$ and
$v:= [G(\gamma -G)]^{(p-1)/p},$ and
 \[ W := \left( \frac{p-1}{p}\right)^{p} \left|\frac{\nabla G}{G(\gamma-G)} \right |_A^{p} |\gamma-2G|^{p-2}[2(p-2)G(\gamma-G)+\gamma^{2}]. \]
\[ W := \left( \frac{p-1}{p}\right)^{p} \left|\frac{\nabla G}{G(\gamma-G)} \right |_A^{p} |\gamma-2G|^{p-2}[2(p-2)G(\gamma-G)+\gamma^{2}]. \]
Then the following Hardy-type inequality holds in ![]() $\Omega ^{*}:$
$\Omega ^{*}:$
and ![]() $W$ is an optimal Hardy-weight of
$W$ is an optimal Hardy-weight of ![]() $-\Delta _{p,A}$ in
$-\Delta _{p,A}$ in ![]() $\Omega ^{*}$. Moreover, up to a multiplicative constant,
$\Omega ^{*}$. Moreover, up to a multiplicative constant, ![]() $v$ is the ground state of
$v$ is the ground state of ![]() $-\Delta _{p,A}-W\mathcal {I}_p$ in
$-\Delta _{p,A}-W\mathcal {I}_p$ in ![]() $\Omega ^{*}$.
$\Omega ^{*}$.
The following simple observation concerns the existence of optimal Hardy-weights for a ‘small perturbation’ of an operator with a given optimal Hardy-weight.
Lemma 2.35 Assume that ![]() $Q_{p,A,V}$ is subcritical in
$Q_{p,A,V}$ is subcritical in ![]() $\Omega$ and admits an optimal Hardy-weight
$\Omega$ and admits an optimal Hardy-weight ![]() $W$ in
$W$ in ![]() $\Omega ^{*} :=\Omega \setminus \{0\}$. Let
$\Omega ^{*} :=\Omega \setminus \{0\}$. Let ![]() $V_1\in M^{q}_{\textrm {loc}}(p;\Omega )$ satisfy
$V_1\in M^{q}_{\textrm {loc}}(p;\Omega )$ satisfy ![]() $V_1\geq -\varepsilon W$ for some
$V_1\geq -\varepsilon W$ for some ![]() $0\leq \varepsilon <1$ and
$0\leq \varepsilon <1$ and ![]() $q>n/p$. Then
$q>n/p$. Then ![]() $W+V_1$ is an optimal Hardy-weight for
$W+V_1$ is an optimal Hardy-weight for ![]() $Q_{p,A,V+V_1}$ in
$Q_{p,A,V+V_1}$ in ![]() $\Omega ^{*}$.
$\Omega ^{*}$.
Proof. Consider the function ![]() $W+ V_1$. Then,
$W+ V_1$. Then, ![]() $Q_{p,A,V+ V_1} - (W+V_1)\mathcal {I}_p=Q_{p,A,V} - W\mathcal {I}_p$ is a critical operator in
$Q_{p,A,V+ V_1} - (W+V_1)\mathcal {I}_p=Q_{p,A,V} - W\mathcal {I}_p$ is a critical operator in ![]() $\Omega ^{*}$.
$\Omega ^{*}$.
Obviously, ![]() $W+V_1\gneqq 0$, and the ground state
$W+V_1\gneqq 0$, and the ground state ![]() $\psi$ of
$\psi$ of ![]() $Q_{p,A,V}-W\mathcal {I}_p$ in
$Q_{p,A,V}-W\mathcal {I}_p$ in ![]() $\Omega ^{*}$ is the ground state of
$\Omega ^{*}$ is the ground state of ![]() $Q_{p,A,V+V_1}-(W+V_1)\mathcal {I}_p$ in
$Q_{p,A,V+V_1}-(W+V_1)\mathcal {I}_p$ in ![]() $\Omega ^{*}$. Moreover,
$\Omega ^{*}$. Moreover,
implying that ![]() $Q_{p,A,V+V_1-(W+V_1)}$ is null-critical in
$Q_{p,A,V+V_1-(W+V_1)}$ is null-critical in ![]() $\Omega ^{*}$ with respect to
$\Omega ^{*}$ with respect to ![]() $W+V_1$. In particular,
$W+V_1$. In particular, ![]() $W+V_1$ is an optimal Hardy-weight of
$W+V_1$ is an optimal Hardy-weight of ![]() $Q_{p,A,V+V_1}$ in
$Q_{p,A,V+V_1}$ in ![]() $\Omega ^{*}$.
$\Omega ^{*}$.
3. Optimal Hardy-weights for indefinite potentials
Lemma 2.35 obviously applies when ![]() $V_1\geq 0$. The main goal in the current section is to obtain optimal Hardy-weights for a general subcritical operator
$V_1\geq 0$. The main goal in the current section is to obtain optimal Hardy-weights for a general subcritical operator ![]() $Q_{p,A,V}$ in a domain
$Q_{p,A,V}$ in a domain ![]() $\Omega$, without assuming
$\Omega$, without assuming ![]() $V= 0$ in
$V= 0$ in ![]() $\Omega$. In particular, we prove theorem 1.1.
$\Omega$. In particular, we prove theorem 1.1.
First, we recall the following weak comparison principle [Reference Pinchover and Psaradakis19, theorem 5.3].
Lemma 3.1 Weak comparison principle
Let ![]() $\Omega \subset \mathbb {R}^{n}$ be a bounded Lipschitz domain. Assume that
$\Omega \subset \mathbb {R}^{n}$ be a bounded Lipschitz domain. Assume that ![]() $A$ is a uniformly elliptic and bounded matrix in
$A$ is a uniformly elliptic and bounded matrix in ![]() $\Omega,$
$\Omega,$ ![]() $V\in M^{q}(p;\Omega )$ and
$V\in M^{q}(p;\Omega )$ and ![]() $0\leq g\in L^{\infty }(\Omega )$. Assume further that
$0\leq g\in L^{\infty }(\Omega )$. Assume further that ![]() $\lambda _1(\Omega )>0,$ where
$\lambda _1(\Omega )>0,$ where ![]() $\lambda _1(\Omega )$ is the principal eigenvalue of the operator
$\lambda _1(\Omega )$ is the principal eigenvalue of the operator ![]() $Q_{p,A,V}$. Let
$Q_{p,A,V}$. Let ![]() $u_2\in W^{1,p}(\Omega )\cap C(\overline {\Omega })$ be a (weak) solution of
$u_2\in W^{1,p}(\Omega )\cap C(\overline {\Omega })$ be a (weak) solution of
 \[ \begin{cases} Q_{p,A,V}(u_2)= g & \text{in } \Omega, \\ u_2>0 & \text{on } \partial \Omega. \end{cases} \]
\[ \begin{cases} Q_{p,A,V}(u_2)= g & \text{in } \Omega, \\ u_2>0 & \text{on } \partial \Omega. \end{cases} \]
If ![]() $u_1\in W^{1,p}(\Omega )\cap C(\overline {\Omega })$ satisfies
$u_1\in W^{1,p}(\Omega )\cap C(\overline {\Omega })$ satisfies
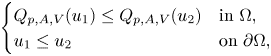 \[ \begin{cases} Q_{p,A,V}(u_1)\leq Q_{p,A,V}(u_2) & \text{in } \Omega, \\ u_1\leq u_2 & \text{on } \partial \Omega, \end{cases} \]
\[ \begin{cases} Q_{p,A,V}(u_1)\leq Q_{p,A,V}(u_2) & \text{in } \Omega, \\ u_1\leq u_2 & \text{on } \partial \Omega, \end{cases} \]
then ![]() $u_1\leq u_2$ in
$u_1\leq u_2$ in ![]() $\Omega$.
$\Omega$.
In the following lemma we generalize the notion of Green potential for ![]() $Q_{p,A,V}$.
$Q_{p,A,V}$.
Lemma 3.2 Assume that ![]() $Q_{p,A,V}$ is subcritical in
$Q_{p,A,V}$ is subcritical in ![]() $\Omega,$ and let
$\Omega,$ and let ![]() $0\lneqq \varphi \in {C_0^{\infty }(\Omega )}$. Then there exists a positive function
$0\lneqq \varphi \in {C_0^{\infty }(\Omega )}$. Then there exists a positive function ![]() $G_{\varphi }\in W^{1,p}_{{\textrm {loc}}}(\Omega ),$ such that
$G_{\varphi }\in W^{1,p}_{{\textrm {loc}}}(\Omega ),$ such that ![]() $G_{\varphi }$ is a positive solution of minimal growth at infinity and satisfies
$G_{\varphi }$ is a positive solution of minimal growth at infinity and satisfies ![]() $Q_{p,A,V}(G_{\varphi }) =\varphi$ in
$Q_{p,A,V}(G_{\varphi }) =\varphi$ in ![]() $\Omega$.
$\Omega$.
Proof. / Fix ![]() $0\lneqq \varphi \in C_0^{\infty }(\Omega )$, and let
$0\lneqq \varphi \in C_0^{\infty }(\Omega )$, and let ![]() $\{ \Omega _k\}_{k\in \mathbb {N}}$ be a smooth exhaustion of
$\{ \Omega _k\}_{k\in \mathbb {N}}$ be a smooth exhaustion of ![]() $\Omega$ with
$\Omega$ with ![]() $\mathrm {supp}(\varphi )\Subset \Omega _1$. Lemma 2.18 implies that there exists a unique positive solution
$\mathrm {supp}(\varphi )\Subset \Omega _1$. Lemma 2.18 implies that there exists a unique positive solution ![]() $G^{k}\in W^{1,p}(\Omega _k)$ to the problem
$G^{k}\in W^{1,p}(\Omega _k)$ to the problem
 \[ \begin{cases} -\Delta_{p,A}(w)+(V+\frac{1}{k})|w|^{p-2}w=\varphi & \text{in } \Omega_k, \\ w=0 & \text{on } \partial \Omega_k. \end{cases} \]
\[ \begin{cases} -\Delta_{p,A}(w)+(V+\frac{1}{k})|w|^{p-2}w=\varphi & \text{in } \Omega_k, \\ w=0 & \text{on } \partial \Omega_k. \end{cases} \]
By the weak comparison principle (lemma 3.1), ![]() $\{ G^{k}\}_{k\in \mathbb {N}}$ is a monotone increasing sequence of functions. Assume first that the sequence
$\{ G^{k}\}_{k\in \mathbb {N}}$ is a monotone increasing sequence of functions. Assume first that the sequence ![]() $\{ G^{k}\}_{k\in \mathbb {N}}$ is not locally uniformly bounded in
$\{ G^{k}\}_{k\in \mathbb {N}}$ is not locally uniformly bounded in ![]() $\Omega$, and let
$\Omega$, and let ![]() $x_1\in \Omega _{2} \setminus \Omega _{1}$. By Harnack's convergence principle there exists a subsequence of
$x_1\in \Omega _{2} \setminus \Omega _{1}$. By Harnack's convergence principle there exists a subsequence of ![]() $\{z_k(x):={G^{k}(x)}/{G^{k}(x_1)} \}_{k\in \mathbb {N}}$ which converges locally uniformly to a positive solution
$\{z_k(x):={G^{k}(x)}/{G^{k}(x_1)} \}_{k\in \mathbb {N}}$ which converges locally uniformly to a positive solution ![]() $G$, of the equation
$G$, of the equation ![]() $Q_{p,A,V}(u)=0$ in
$Q_{p,A,V}(u)=0$ in ![]() $\Omega$. Therefore,
$\Omega$. Therefore, ![]() $G$ is a positive solution of the equation
$G$ is a positive solution of the equation ![]() $Q_{p,A,V}(u)=0$ in
$Q_{p,A,V}(u)=0$ in ![]() $\Omega$ which clearly has minimal growth in a neighborhood of infinity in
$\Omega$ which clearly has minimal growth in a neighborhood of infinity in ![]() $\Omega$, i.e.,
$\Omega$, i.e., ![]() $G$ is a ground state. This is a contradiction to the subcriticality of the operator
$G$ is a ground state. This is a contradiction to the subcriticality of the operator ![]() $Q_{p,A,V}$ in
$Q_{p,A,V}$ in ![]() $\Omega$.
$\Omega$.
Consequently, Harnack inequality ([Reference Pinchover and Psaradakis19, theorem 2.7]) implies that the sequence ![]() $\{ G^{k}\}_{k\in \mathbb {N}}$ is locally uniformly bounded in
$\{ G^{k}\}_{k\in \mathbb {N}}$ is locally uniformly bounded in ![]() $\Omega$. By Harnack convergence principle and the strong maximum principle, it converges locally uniformly (up to a subsequence) to a positive solution,
$\Omega$. By Harnack convergence principle and the strong maximum principle, it converges locally uniformly (up to a subsequence) to a positive solution, ![]() $G_{\varphi }$, of the equation
$G_{\varphi }$, of the equation ![]() $Q_{p,A,V}(u)=\varphi$ in
$Q_{p,A,V}(u)=\varphi$ in ![]() $\Omega$. In fact, [Reference Lieberman16, theorem 5.3] implies that there exists
$\Omega$. In fact, [Reference Lieberman16, theorem 5.3] implies that there exists ![]() $0<\alpha <1$ such that
$0<\alpha <1$ such that ![]() $G_{\varphi } \in C^{1,\alpha }_{{\textrm {loc}}}(\Omega )$.
$G_{\varphi } \in C^{1,\alpha }_{{\textrm {loc}}}(\Omega )$.
Definition 3.3 Let ![]() $0\lneqq \varphi \in {C_0^{\infty }(\Omega )}$. A positive solution
$0\lneqq \varphi \in {C_0^{\infty }(\Omega )}$. A positive solution ![]() $u \in G_{\varphi }\in \mathcal {MG}_{A,V,\Omega, \textrm{supp}\,(\varphi )}$ that satisfies
$u \in G_{\varphi }\in \mathcal {MG}_{A,V,\Omega, \textrm{supp}\,(\varphi )}$ that satisfies ![]() $Q_{p,A,V}(u)=\varphi$ in
$Q_{p,A,V}(u)=\varphi$ in ![]() $\Omega$, is called a Green potential of
$\Omega$, is called a Green potential of ![]() $Q_{p,A,V}$ in
$Q_{p,A,V}$ in ![]() $\Omega$ with a density
$\Omega$ with a density ![]() $\varphi$.
$\varphi$.
We proceed with the following technical proposition (cf. [Reference Devyver and Pinchover9, lemma 2.10]).
Proposition 3.4 Let ![]() $f(t)\in C^{2}(\mathbb {R}_+)$ satisfying
$f(t)\in C^{2}(\mathbb {R}_+)$ satisfying ![]() $f,\,f',\,-f''>0$. Then, for all
$f,\,f',\,-f''>0$. Then, for all ![]() $0\leq u\in C^{1}(\Omega )$
$0\leq u\in C^{1}(\Omega )$
 \begin{align*} Q_{p,A,V}(f(u)) & ={-}\Delta_p^{1D}(f)(u)|\nabla u|^{p}_A+(f'(u))^{p-1} \\ & \quad \times \left(-\Delta_{p,A}(u) + V\left(\frac{f(u)}{f'(u) u}\right)^{p-1} |u|^{p-1}\right) \end{align*}
\begin{align*} Q_{p,A,V}(f(u)) & ={-}\Delta_p^{1D}(f)(u)|\nabla u|^{p}_A+(f'(u))^{p-1} \\ & \quad \times \left(-\Delta_{p,A}(u) + V\left(\frac{f(u)}{f'(u) u}\right)^{p-1} |u|^{p-1}\right) \end{align*}
in the weak sense. Here ![]() $-\Delta _p^{1D} f(t):=-(|f'(t)|^{p-2}f'(t))'$ is the one-dimensional
$-\Delta _p^{1D} f(t):=-(|f'(t)|^{p-2}f'(t))'$ is the one-dimensional ![]() $p$-Laplacian.
$p$-Laplacian.
Proof. By [Reference Devyver and Pinchover9, lemma 2.10] (which clearly holds for the ![]() $(p,\,A)$-Laplacian), we have:
$(p,\,A)$-Laplacian), we have:
in the weak sense. Since ![]() $f\in C^{2},\,f,\,f',\,-f''>0$ we have
$f\in C^{2},\,f,\,f',\,-f''>0$ we have
and together with (3.1) the proposition is proved.
Remark 3.5 We remark that if ![]() $f(t)=t^{\frac {p-1}{p}}$, then
$f(t)=t^{\frac {p-1}{p}}$, then
Lemma 3.2 and proposition 3.4 imply:
Corollary 3.6 Assume that ![]() $Q_{p,A,c_p V}$ is subcritical in
$Q_{p,A,c_p V}$ is subcritical in ![]() $\Omega$. For
$\Omega$. For ![]() $0\lneq \varphi \in {C_0^{\infty }(\Omega )},$ let
$0\lneq \varphi \in {C_0^{\infty }(\Omega )},$ let ![]() $G_{\varphi }$ be a Green potential satisfying
$G_{\varphi }$ be a Green potential satisfying ![]() $Q_{p,A,c_p V}(G_{\varphi })=\varphi$ in
$Q_{p,A,c_p V}(G_{\varphi })=\varphi$ in ![]() $\Omega,$ and let
$\Omega,$ and let ![]() $f(t)=t^{\frac {p-1}{p}}$. Then,
$f(t)=t^{\frac {p-1}{p}}$. Then,
In particular, ![]() $f(G_{\varphi })$ is a positive solution of the equation
$f(G_{\varphi })$ is a positive solution of the equation ![]() $Q_{p,A,V-W}(v) =0,$ where
$Q_{p,A,V-W}(v) =0,$ where
The following lemma is a generalization of lemma 2.33 to the case ![]() $V\neq 0$.
$V\neq 0$.
Lemma 3.7 Assume that ![]() $Q_{p,A,V}$ is subcritical in
$Q_{p,A,V}$ is subcritical in ![]() $\Omega,$ and let
$\Omega,$ and let ![]() $G_{\varphi }\in C^{1,\alpha }_{{\textrm {loc}}}(\Omega )$ be a Green potential (with respect to
$G_{\varphi }\in C^{1,\alpha }_{{\textrm {loc}}}(\Omega )$ be a Green potential (with respect to ![]() $0\lneq \varphi \in {C_0^{\infty }(\Omega )}$), and assume that
$0\lneq \varphi \in {C_0^{\infty }(\Omega )}$), and assume that
Then, there exists ![]() $0< M_{\varphi }<\sup \limits _{\Omega }G_{\varphi }$ such that for almost every
$0< M_{\varphi }<\sup \limits _{\Omega }G_{\varphi }$ such that for almost every ![]() $0< t< M_{\varphi },$ satisfying
$0< t< M_{\varphi },$ satisfying
there exists ![]() $C>0,$ independent of
$C>0,$ independent of ![]() $t,$ such that
$t,$ such that
where ![]() $\mathrm {d} \sigma _A=\frac {|\nabla G_{\varphi }|_A}{|\nabla G_{\varphi }|}\, \,\mathrm {d}\mathcal {H}^{n-1},$
$\mathrm {d} \sigma _A=\frac {|\nabla G_{\varphi }|_A}{|\nabla G_{\varphi }|}\, \,\mathrm {d}\mathcal {H}^{n-1},$ ![]() $\mathcal {H}^{n-1}$-a.e.
$\mathcal {H}^{n-1}$-a.e.
Proof. The assumption ![]() $\lim \limits _{x\to \overline {\infty }}G_{\varphi }=0,$ and proposition imply that for a.e.
$\lim \limits _{x\to \overline {\infty }}G_{\varphi }=0,$ and proposition imply that for a.e. ![]() $t>0$ the set
$t>0$ the set ![]() $\Omega _t$ has finite perimeter. Furthermore, (3.3) implies that
$\Omega _t$ has finite perimeter. Furthermore, (3.3) implies that ![]() $|V|G_{\varphi }^{p-1}\in \mathcal {M}(\Omega ')$. Finally, Sard's theorem for
$|V|G_{\varphi }^{p-1}\in \mathcal {M}(\Omega ')$. Finally, Sard's theorem for ![]() $C^{1,\alpha }$-functions implies that the conditions in Gauss–Green theorem (lemma 2.5) are satisfied in
$C^{1,\alpha }$-functions implies that the conditions in Gauss–Green theorem (lemma 2.5) are satisfied in ![]() $\Omega '$. Hence,
$\Omega '$. Hence,
 \begin{align*} \int_{\Omega_t}(\varphi -V|G_{\varphi}|^{p-2}G_{\varphi}) \,\mathrm{d}x & ={-}\int_{\Omega_t}\mathrm{div} (|\nabla G_{\varphi}|_A^{p-2} A\nabla G_{\varphi}) \,\mathrm{d}x \\ & ={-} \int_{\partial \Omega_t} |\nabla G_{\varphi}|_A^{p-2} A\nabla G_{\varphi} \cdot \vec{n} \,\mathrm{d}\mathcal{H}^{n-1}. \end{align*}
\begin{align*} \int_{\Omega_t}(\varphi -V|G_{\varphi}|^{p-2}G_{\varphi}) \,\mathrm{d}x & ={-}\int_{\Omega_t}\mathrm{div} (|\nabla G_{\varphi}|_A^{p-2} A\nabla G_{\varphi}) \,\mathrm{d}x \\ & ={-} \int_{\partial \Omega_t} |\nabla G_{\varphi}|_A^{p-2} A\nabla G_{\varphi} \cdot \vec{n} \,\mathrm{d}\mathcal{H}^{n-1}. \end{align*}
The assumptions ![]() $\lim \limits _{x\to \overline {\infty }}G_{\varphi }=0,$ and
$\lim \limits _{x\to \overline {\infty }}G_{\varphi }=0,$ and ![]() $\int _{\Omega }VG_{\varphi }^{p-1} \,\mathrm {d}x< 0$ imply that there exists a sufficiently small
$\int _{\Omega }VG_{\varphi }^{p-1} \,\mathrm {d}x< 0$ imply that there exists a sufficiently small ![]() $M_{\varphi }>0$ such that for a.e
$M_{\varphi }>0$ such that for a.e ![]() $0< t< M_{\varphi }$,
$0< t< M_{\varphi }$,
Moreover, the assumption ![]() $\text {supp}(\varphi )\Subset \Omega _t$ implies
$\text {supp}(\varphi )\Subset \Omega _t$ implies
Consequently,
and ![]() $C$ does not depend on
$C$ does not depend on ![]() $t$. Sard's theorem for
$t$. Sard's theorem for ![]() $C^{1,\alpha }$ functions implies that for
$C^{1,\alpha }$ functions implies that for ![]() $\mathcal {H}^{n-1}$-a.e.
$\mathcal {H}^{n-1}$-a.e. ![]() $x\in \partial \Omega '$,
$x\in \partial \Omega '$, ![]() $|\nabla G(x)|\neq 0$. Furthermore, the definition of
$|\nabla G(x)|\neq 0$. Furthermore, the definition of ![]() $\Omega '$ implies that
$\Omega '$ implies that ![]() $G_{\varphi }\geq t$ in
$G_{\varphi }\geq t$ in ![]() $\Omega '$, and hence,
$\Omega '$, and hence, ![]() $\vec {n}=-\frac {\nabla G_{\varphi }}{|\nabla G_{\varphi }|}$ for
$\vec {n}=-\frac {\nabla G_{\varphi }}{|\nabla G_{\varphi }|}$ for ![]() $\mathcal {H}^{n-1}$-a.e.
$\mathcal {H}^{n-1}$-a.e. ![]() $x\in \partial \Omega '$. Therefore,
$x\in \partial \Omega '$. Therefore,
Remark 3.8 Th e assumption ![]() $\int _{\Omega }VG_{\varphi }^{p-1} \,\mathrm {d}x< 0$ in lemma 3.7 is needed for arguing (3.5). In particular, the lemma still holds once assuming instead that
$\int _{\Omega }VG_{\varphi }^{p-1} \,\mathrm {d}x< 0$ in lemma 3.7 is needed for arguing (3.5). In particular, the lemma still holds once assuming instead that ![]() $V\leq 0$ in
$V\leq 0$ in ![]() $\Omega$.
$\Omega$.
We proceed with the following lemma.
Lemma 3.9 cf. [Reference Devyver and Pinchover9, propositions 5.1 and 5.5]
Let ![]() $0\lneqq \varphi \in {C_0^{\infty }(\Omega )},$ and assume that
$0\lneqq \varphi \in {C_0^{\infty }(\Omega )},$ and assume that ![]() $Q_{p,A,c_p V}$ is subcritical in
$Q_{p,A,c_p V}$ is subcritical in ![]() $\Omega$. Let
$\Omega$. Let ![]() $G_{\varphi }\in C^{1,\alpha }_{{\textrm {loc}}}(\Omega )$ be a Green potential satisfying
$G_{\varphi }\in C^{1,\alpha }_{{\textrm {loc}}}(\Omega )$ be a Green potential satisfying ![]() $Q_{p,A,c_pV}(G_{\varphi })=\varphi \quad \text {in } \Omega,$ and assume that
$Q_{p,A,c_pV}(G_{\varphi })=\varphi \quad \text {in } \Omega,$ and assume that
Consider the function ![]() $f(t)=t^{\frac {p-1}{p}},$ and let
$f(t)=t^{\frac {p-1}{p}},$ and let
Then ![]() $Q_{p,A,V-W}$ is critical in
$Q_{p,A,V-W}$ is critical in ![]() $\Omega,$ with a ground state
$\Omega,$ with a ground state ![]() $f(G_{\varphi })$ and
$f(G_{\varphi })$ and ![]() $\int _{\Omega }Wf(G_{\varphi })^{p} \,\mathrm {d}x=\infty$. Hence,
$\int _{\Omega }Wf(G_{\varphi })^{p} \,\mathrm {d}x=\infty$. Hence, ![]() $W$ is an optimal Hardy-weight for
$W$ is an optimal Hardy-weight for ![]() $Q_{p,A,V}$ in
$Q_{p,A,V}$ in ![]() $\Omega.$
$\Omega.$
Proof. Criticality: Notice that ![]() $c_p>1$. and therefore,
$c_p>1$. and therefore, ![]() $Q_{p,A,V}$ is subcritical in
$Q_{p,A,V}$ is subcritical in ![]() $\Omega$ [Reference Pinchover and Psaradakis19, Corollary 4.17]. Let
$\Omega$ [Reference Pinchover and Psaradakis19, Corollary 4.17]. Let ![]() $M_{\varphi }$ be given by lemma 3.7, and let
$M_{\varphi }$ be given by lemma 3.7, and let ![]() $K\Subset \Omega$ be a precompact smooth subdomain satisfying
$K\Subset \Omega$ be a precompact smooth subdomain satisfying ![]() $\text {supp} \, \varphi \Subset K$,
$\text {supp} \, \varphi \Subset K$, ![]() $\max \limits _{\Omega \setminus K}G_{\varphi }< M_{\varphi }$ and
$\max \limits _{\Omega \setminus K}G_{\varphi }< M_{\varphi }$ and ![]() $G_{\varphi }<1$ for all
$G_{\varphi }<1$ for all ![]() $x\in \Omega \setminus K$. Assume without loss of generality that
$x\in \Omega \setminus K$. Assume without loss of generality that ![]() $\inf \limits _{K}G_{\varphi }\geq 1$.
$\inf \limits _{K}G_{\varphi }\geq 1$.
For each ![]() $k\in \mathbb {N}$, consider the function
$k\in \mathbb {N}$, consider the function ![]() $\phi _k(f(G_{\varphi }))$, where
$\phi _k(f(G_{\varphi }))$, where ![]() $f(t)=t^{\frac {p-1}{p}}$ and
$f(t)=t^{\frac {p-1}{p}}$ and
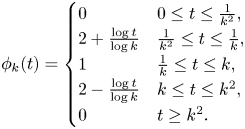 \[ \phi_k(t)= \begin{cases} 0 & 0 \leq t\leq \frac{1}{k^{2}},\\ 2+\frac{\log t}{\log k} & \frac{1}{k^{2}} \leq t\leq \frac{1}{k},\\ 1 & \frac{1}{k}\leq t \leq k,\\ 2-\frac{\log t}{\log k} & k \leq t\leq k^{2},\\ 0 & t \geq k^{2}. \end{cases} \]
\[ \phi_k(t)= \begin{cases} 0 & 0 \leq t\leq \frac{1}{k^{2}},\\ 2+\frac{\log t}{\log k} & \frac{1}{k^{2}} \leq t\leq \frac{1}{k},\\ 1 & \frac{1}{k}\leq t \leq k,\\ 2-\frac{\log t}{\log k} & k \leq t\leq k^{2},\\ 0 & t \geq k^{2}. \end{cases} \]
We claim that ![]() $u_k= \phi _k(f(G_{\varphi }))f(G_{\varphi })$ is a null-sequence of
$u_k= \phi _k(f(G_{\varphi }))f(G_{\varphi })$ is a null-sequence of ![]() $Q_{p,A,V-W}$ in
$Q_{p,A,V-W}$ in ![]() $\Omega$. Indeed, by (2.2),
$\Omega$. Indeed, by (2.2), ![]() $\mathcal {Q}_{\mathrm {sim}}(w)\asymp \mathcal {Q}(wf(G_{\varphi })) = \mathcal {Q}(u)$, where
$\mathcal {Q}_{\mathrm {sim}}(w)\asymp \mathcal {Q}(wf(G_{\varphi })) = \mathcal {Q}(u)$, where
and
Moreover, by corollary 2.28 we have
 \[ \mathcal{Q}_{\text{sim}}(w)\leq \begin{cases} CX(w) & 1< p\leq 2, \\ C \left[ X(w)+X(w)^{2/p}Y(w)^{\frac{p-2}{p}}\right] & p>2, \end{cases} \]
\[ \mathcal{Q}_{\text{sim}}(w)\leq \begin{cases} CX(w) & 1< p\leq 2, \\ C \left[ X(w)+X(w)^{2/p}Y(w)^{\frac{p-2}{p}}\right] & p>2, \end{cases} \]where
By the (classical) coarea formula ([Reference Chen, Torres and Ziemer7, theorem 2.32]),
 \begin{align*} &X(\phi_k(f(G_{\varphi})))=\int_{\Omega\setminus K} f(G_{\varphi})^{p}|\phi_k'(f(G_{\varphi}))|^{p}|f'(G_{\varphi})|^{p}|\nabla G_{\varphi}|_A^{p} \,\mathrm{d}x\\ &\quad=\int_{0}^{\max\limits_{\Omega\setminus K}G_{\varphi}}f(t)^{p}|\phi_k'(f(t))|^{p}f'(t)^{p}\,\mathrm{d}t\int_{G_{\varphi}=t} |\nabla G_{\varphi}|_A^{p-1}\text{d} \sigma_A. \end{align*}
\begin{align*} &X(\phi_k(f(G_{\varphi})))=\int_{\Omega\setminus K} f(G_{\varphi})^{p}|\phi_k'(f(G_{\varphi}))|^{p}|f'(G_{\varphi})|^{p}|\nabla G_{\varphi}|_A^{p} \,\mathrm{d}x\\ &\quad=\int_{0}^{\max\limits_{\Omega\setminus K}G_{\varphi}}f(t)^{p}|\phi_k'(f(t))|^{p}f'(t)^{p}\,\mathrm{d}t\int_{G_{\varphi}=t} |\nabla G_{\varphi}|_A^{p-1}\text{d} \sigma_A. \end{align*}
By lemma 3.7, for a.e. ![]() $0< t<\max \limits _{\Omega \setminus K}G_{\varphi }$ we have
$0< t<\max \limits _{\Omega \setminus K}G_{\varphi }$ we have ![]() $\int _{G_{\varphi }=t} |\nabla G_{\varphi }|_A^{p-1}\text {d} \sigma _A \asymp 1$. Moreover,
$\int _{G_{\varphi }=t} |\nabla G_{\varphi }|_A^{p-1}\text {d} \sigma _A \asymp 1$. Moreover,
 \begin{align*} \int_{0}^{\max\limits_{\Omega\setminus K}G_{\varphi}} f(t)^{p}|\phi_k'(f(t))|^{p}f'(t)^{p}\,\mathrm{d}t&= C(p)\int_0^{f(\max\limits_{\Omega\setminus K}G_{\varphi})} \frac{|s\phi_k'(s)|^{p}}{s}\,\mathrm{d}s\\ &=\frac{C(p)}{\log^{p} k}\int_{\frac 1{k^{2}}}^{\frac 1k}\frac{1}{s} \,\mathrm{d}s\asymp \left(\frac{1}{\log k} \right)^{p-1}. \end{align*}
\begin{align*} \int_{0}^{\max\limits_{\Omega\setminus K}G_{\varphi}} f(t)^{p}|\phi_k'(f(t))|^{p}f'(t)^{p}\,\mathrm{d}t&= C(p)\int_0^{f(\max\limits_{\Omega\setminus K}G_{\varphi})} \frac{|s\phi_k'(s)|^{p}}{s}\,\mathrm{d}s\\ &=\frac{C(p)}{\log^{p} k}\int_{\frac 1{k^{2}}}^{\frac 1k}\frac{1}{s} \,\mathrm{d}s\asymp \left(\frac{1}{\log k} \right)^{p-1}. \end{align*}
Consequently, ![]() $X(\phi _n(f(G_{\varphi })))\asymp (\dfrac {1}{\log k})^{p-1}$. By a similar calculation,
$X(\phi _n(f(G_{\varphi })))\asymp (\dfrac {1}{\log k})^{p-1}$. By a similar calculation,
 \begin{align*} &Y(\phi_k(f(G_{\varphi})))=\int_{\Omega\setminus K}|\phi_k(f(G_{\varphi}))|^{p}f'(G_{\varphi})^{p}|\nabla G_{\varphi}|_A^{p} \,\mathrm{d}x\asymp \int_{0}^{1}|\phi_k(f(t))|^{p}f'(t)^{p} \,\mathrm{d}t \asymp\\ &\int_{0}^{f(1)}|\phi_k(s)|^{p}\frac{ds}{s}= \int_{1/k^{2}}^{1/k}\left ( 2+\frac{\log s}{\log k}\right)\frac{1}{s} \,\mathrm{d}s+\int_{1/k}^{1}\frac{1}{s}\,\mathrm{d}s \asymp \int_{1/k}^{1}\frac{1}{s} \,\mathrm{d}s\asymp \log k . \end{align*}
\begin{align*} &Y(\phi_k(f(G_{\varphi})))=\int_{\Omega\setminus K}|\phi_k(f(G_{\varphi}))|^{p}f'(G_{\varphi})^{p}|\nabla G_{\varphi}|_A^{p} \,\mathrm{d}x\asymp \int_{0}^{1}|\phi_k(f(t))|^{p}f'(t)^{p} \,\mathrm{d}t \asymp\\ &\int_{0}^{f(1)}|\phi_k(s)|^{p}\frac{ds}{s}= \int_{1/k^{2}}^{1/k}\left ( 2+\frac{\log s}{\log k}\right)\frac{1}{s} \,\mathrm{d}s+\int_{1/k}^{1}\frac{1}{s}\,\mathrm{d}s \asymp \int_{1/k}^{1}\frac{1}{s} \,\mathrm{d}s\asymp \log k . \end{align*}
It follows that ![]() $\mathcal {Q}_{\mathrm {sim}}(w_k)=\mathcal {Q}_{\mathrm {sim}}(\phi _k(f(G_{\varphi })))\to 0$ as
$\mathcal {Q}_{\mathrm {sim}}(w_k)=\mathcal {Q}_{\mathrm {sim}}(\phi _k(f(G_{\varphi })))\to 0$ as ![]() $k \to \infty$, and therefore,
$k \to \infty$, and therefore,
Let us specialize ![]() $\varepsilon _0>0$ such that the set
$\varepsilon _0>0$ such that the set ![]() $B=\{x\in \Omega : \varepsilon _0/2< f(G_{\varphi })<\varepsilon _0 \}$ is nonempty, bounded, and contained in
$B=\{x\in \Omega : \varepsilon _0/2< f(G_{\varphi })<\varepsilon _0 \}$ is nonempty, bounded, and contained in ![]() $\Omega \setminus K.$ Therefore,
$\Omega \setminus K.$ Therefore,
Thus, the sequence ![]() $\{u_k\}$ is a null-sequence, and in light of lemma 2.25,
$\{u_k\}$ is a null-sequence, and in light of lemma 2.25, ![]() $Q_{p,A,V-W}$ is critical in
$Q_{p,A,V-W}$ is critical in ![]() $\Omega$.
$\Omega$.
Null-criticality: Let ![]() $K\Subset \Omega$ be a precompact smooth subdomain as in the first part of the proof.
$K\Subset \Omega$ be a precompact smooth subdomain as in the first part of the proof.
For almost every ![]() $0<\tau <1$ we consider the set
$0<\tau <1$ we consider the set ![]() $\Omega _{\tau }:=\{x\in \Omega \mid \tau < G_{\varphi }<\min \limits _{K}G_{\varphi } \}$ which has finite perimeter. Recall that
$\Omega _{\tau }:=\{x\in \Omega \mid \tau < G_{\varphi }<\min \limits _{K}G_{\varphi } \}$ which has finite perimeter. Recall that
By the (classical) coarea formula and (3.4),
 \begin{align*} &\int _{\Omega_{\tau}}W(f(G_{\varphi}))^{p} \,\mathrm{d}x= \left(\frac{p-1}{p}\right)^{p}\int _{\Omega_{\tau}}\frac{|\nabla G_{\varphi}|_A^{p}}{G_{\varphi}^{p}}(f(G_{\varphi}))^{p} \,\mathrm{d}x\\ &\quad=\left( \frac{p-1}{p}\right)^{p}\int_{\mathbb{R}_+}\left(\frac{f(t)}{t} \right)^{p} \,\mathrm{d}t \int _{G_{\varphi=t}}|\nabla G_{\varphi}|_A^{p-1} \text{d}\sigma_A\asymp C \int_{\tau}^{\min\limits_K G_{\varphi}} \left(\frac{f(t)}{t} \right)^{p} \,\mathrm{d}t. \end{align*}
\begin{align*} &\int _{\Omega_{\tau}}W(f(G_{\varphi}))^{p} \,\mathrm{d}x= \left(\frac{p-1}{p}\right)^{p}\int _{\Omega_{\tau}}\frac{|\nabla G_{\varphi}|_A^{p}}{G_{\varphi}^{p}}(f(G_{\varphi}))^{p} \,\mathrm{d}x\\ &\quad=\left( \frac{p-1}{p}\right)^{p}\int_{\mathbb{R}_+}\left(\frac{f(t)}{t} \right)^{p} \,\mathrm{d}t \int _{G_{\varphi=t}}|\nabla G_{\varphi}|_A^{p-1} \text{d}\sigma_A\asymp C \int_{\tau}^{\min\limits_K G_{\varphi}} \left(\frac{f(t)}{t} \right)^{p} \,\mathrm{d}t. \end{align*}
By letting ![]() $\tau \to 0$ we obtain that
$\tau \to 0$ we obtain that ![]() $\int _{\Omega \setminus K}Wf(G_{\varphi })^{p} \,\mathrm {d}x=\infty.$
$\int _{\Omega \setminus K}Wf(G_{\varphi })^{p} \,\mathrm {d}x=\infty.$
Remark 3.10 Remark 3.8 implies that lemma 3.9 still holds if one assumes ![]() $V\leq 0$ in
$V\leq 0$ in ![]() $\Omega$ instead of the assumption
$\Omega$ instead of the assumption ![]() $\int _{\Omega }VG_{\varphi }^{p-1} \,\mathrm {d}x< 0$.
$\int _{\Omega }VG_{\varphi }^{p-1} \,\mathrm {d}x< 0$.
Proof of theorem 1.1. Notice that ![]() $c_p > 1$, and hence
$c_p > 1$, and hence ![]() $Q_{p,A,{V}/{c_p}}$ is subcritical in
$Q_{p,A,{V}/{c_p}}$ is subcritical in ![]() $\Omega$. Let
$\Omega$. Let ![]() $G_{\varphi }$ be the Green potential of
$G_{\varphi }$ be the Green potential of ![]() $Q_{p,A,V}$, given by lemma 3.2. By lemma 3.9, the operator
$Q_{p,A,V}$, given by lemma 3.2. By lemma 3.9, the operator ![]() $Q_{p,A,{V}/{c_p}}$ admits an optimal Hardy-weight in
$Q_{p,A,{V}/{c_p}}$ admits an optimal Hardy-weight in ![]() $\Omega$.
$\Omega$.
Proof of corollary 1.2. Notice that ![]() $c_p > 1$, and hence
$c_p > 1$, and hence ![]() $Q_{p,A,{V}/{c_p}}$ is subcritical in
$Q_{p,A,{V}/{c_p}}$ is subcritical in ![]() $\Omega$. Let
$\Omega$. Let ![]() $G_{\varphi }$ be the Green potential of
$G_{\varphi }$ be the Green potential of ![]() $Q_{p,A,V}$, given by lemma 3.2. By the minimal growth property of
$Q_{p,A,V}$, given by lemma 3.2. By the minimal growth property of ![]() $G_{\varphi }$, for any
$G_{\varphi }$, for any ![]() $x_0\in K\Subset \Omega$,
$x_0\in K\Subset \Omega$, ![]() $G_{\varphi }\leq CG$ in
$G_{\varphi }\leq CG$ in ![]() $\Omega \setminus K$, and in particular,
$\Omega \setminus K$, and in particular,
By lemma 3.9 and remark 3.10, the operator ![]() $Q_{p,A,{V}/{c_p}}$ admits an optimal Hardy-weight in
$Q_{p,A,{V}/{c_p}}$ admits an optimal Hardy-weight in ![]() $\Omega$.
$\Omega$.
Corollary 1.2 and the following remark give rise to new optimal Hardy-type inequalities in the smooth case.
Remark 3.11 Let ![]() $\Omega \subset \mathbb {R}^{n}$ be a domain and let
$\Omega \subset \mathbb {R}^{n}$ be a domain and let ![]() $Q_{p,A,V}$ be a subcritical operator in
$Q_{p,A,V}$ be a subcritical operator in ![]() $\Omega$ satisfying assumptions 2.8. Assume further that
$\Omega$ satisfying assumptions 2.8. Assume further that ![]() $V\leq 0$ in
$V\leq 0$ in ![]() $\Omega$. Then, there exists
$\Omega$. Then, there exists ![]() $K\Subset \Omega$ and
$K\Subset \Omega$ and ![]() $x_0\in \mathrm {int} K \Subset \Omega$, such that the operator
$x_0\in \mathrm {int} K \Subset \Omega$, such that the operator ![]() $Q_{p,A,V}$ admits a positive solution
$Q_{p,A,V}$ admits a positive solution ![]() $G(x)$ in
$G(x)$ in ![]() $\Omega \setminus \{x_0\}$ satisfying (1.2) in each of the following cases :
$\Omega \setminus \{x_0\}$ satisfying (1.2) in each of the following cases :
•
 $A$ is a constant, symmetric, positive definite matrix;
$A$ is a constant, symmetric, positive definite matrix;  $V\in L^{\infty }(\Omega )$;
$V\in L^{\infty }(\Omega )$;  $\Omega$ is a bounded
$\Omega$ is a bounded  $C^{1,\alpha }$ domain and
$C^{1,\alpha }$ domain and  $\lambda _1(\Omega )>0$ [Reference Lieberman17].
$\lambda _1(\Omega )>0$ [Reference Lieberman17].•
 $A$ is a constant, symmetric, positive definite matrix;
$A$ is a constant, symmetric, positive definite matrix;  $V\in C_0^{\infty }(\mathbb {R}^{n})$;
$V\in C_0^{\infty }(\mathbb {R}^{n})$;  $\Omega =\mathbb {R}^{n}$ [Reference Fraas and Pinchover12, Reference Giri and Pinchover13].
$\Omega =\mathbb {R}^{n}$ [Reference Fraas and Pinchover12, Reference Giri and Pinchover13].
In particular, theorem 1.1 can be applied in each of the latter cases.
Acknowledgments
The paper is based on part of the author's Ph.D. thesis. The author expresses his gratitude to his thesis adviser, Professor Yehuda Pinchover, for the encouragement, support and help he gave him. The author is grateful to the Technion for supporting his study.