In this paper, we prove results about solutions of the Diophantine equation 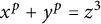 $x^p+y^p=z^3$ over various number fields using the modular method. First, by assuming some standard modularity conjecture, we prove an asymptotic result for general number fields of narrow class number one satisfying some technical conditions. Second, we show that there is an explicit bound such that the equation
$x^p+y^p=z^3$ over various number fields using the modular method. First, by assuming some standard modularity conjecture, we prove an asymptotic result for general number fields of narrow class number one satisfying some technical conditions. Second, we show that there is an explicit bound such that the equation 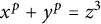 $x^p+y^p=z^3$ does not have a particular type of solution over
$x^p+y^p=z^3$ does not have a particular type of solution over 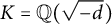 $K=\mathbb {Q}(\sqrt {-d})$, where
$K=\mathbb {Q}(\sqrt {-d})$, where 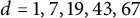 $d=1,7,19,43,67$ whenever p is bigger than this bound. During the course of the proof, we prove various results about the irreducibility of Galois representations, image of inertia groups, and Bianchi newforms.
$d=1,7,19,43,67$ whenever p is bigger than this bound. During the course of the proof, we prove various results about the irreducibility of Galois representations, image of inertia groups, and Bianchi newforms.
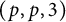 $(p,p,\text{3})$ over number fields
$(p,p,\text{3})$ over number fields