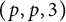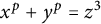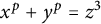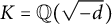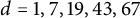1 Introduction
Solving Diophantine equations is one of the oldest and widely studied topics in number theory. Yet we still do not have a general method that would allow us to produce solutions of a given Diophantine equation. Most of the time, it may be easier to show the nonexistence of solutions, but even this can be quite challenging as it was the case for the proof of Fermat’s Last Theorem (FLT). The method to solve the Fermat equation, used by Wiles in his famous proof, can be adapted to solve similar Fermat-type equations. This strategy, which is referred as the “modular method,” starts with an elliptic curve attached to a putative solution of the given equation. Then, using many celebrated theorems of the area, the problem can be reduced to one of the following: computing newforms of a certain level, or computing all elliptic curves of a given conductor with particular information about torsion subgroup and rational isogeny, or computing all solutions to an S-unit equation. Neither of these computations are easy in general. Especially if one needs to prove Fermat’s theorem over a number field other than rationals, some fundamental theorems that go into the proof now become conjectures only, such as the modularity conjecture. Recently, there has been much progress in several different generalizations of this famous result. For instance, in [Reference Freitas and Siksek12], Freitas and Siksek proved the asymptotic FLT for certain totally real fields K. That is, they showed that there is a constant
![]() $B_K$
such that, for any prime
$B_K$
such that, for any prime
![]() $p>B_K$
, the only solutions to the Fermat equation
$p>B_K$
, the only solutions to the Fermat equation
![]() $a^p+b^p+c^p=0$
where
$a^p+b^p+c^p=0$
where
![]() $a,b,c \in {\mathcal O}_{K}$
are the trivial ones satisfying
$a,b,c \in {\mathcal O}_{K}$
are the trivial ones satisfying
![]() $abc=0$
. Then, Deconinck [Reference Deconinck7] extended the results of Freitas and Siksek [Reference Freitas and Siksek12] to the generalized Fermat equation of the form
$abc=0$
. Then, Deconinck [Reference Deconinck7] extended the results of Freitas and Siksek [Reference Freitas and Siksek12] to the generalized Fermat equation of the form
![]() $Aa^p+Bb^p+Cc^p=0$
where
$Aa^p+Bb^p+Cc^p=0$
where
![]() $A,B,C$
are odd integers belonging to a totally real field. Later, in [Reference Şengün and Siksek27], Şengün and Siksek proved the asymptotic FLT for any number field K by assuming modularity. This result has been generalized by Kara and Ozman in [Reference Kara and Ozman17] to the case of the generalized Fermat equation. Moreover, recently, in [Reference Ţurcaş31, Reference Ţurcaş32], Turcas studied the Fermat equation over imaginary quadratic fields
$A,B,C$
are odd integers belonging to a totally real field. Later, in [Reference Şengün and Siksek27], Şengün and Siksek proved the asymptotic FLT for any number field K by assuming modularity. This result has been generalized by Kara and Ozman in [Reference Kara and Ozman17] to the case of the generalized Fermat equation. Moreover, recently, in [Reference Ţurcaş31, Reference Ţurcaş32], Turcas studied the Fermat equation over imaginary quadratic fields
![]() ${\mathbb Q}(\sqrt {-d})$
with class number one.
${\mathbb Q}(\sqrt {-d})$
with class number one.
Similar generalizations are quite rare for other Fermat-type equations such as
![]() $x^p+y^q=z^r$
. The solutions of this equation have been studied over rationals by many mathematicians including Darmon, Merel, Bennett, and Poonen. Several mathematicians have worked on similar Fermat-type equations with different exponents over rational numbers. We have summarized these results in [Reference Işik, Kara and Ozman14]; therefore, we will not repeat them here, but we want to mention that not many results exist for generalizations of these to higher degree number fields. During the write-up of this paper, we have been informed about the work of Mocanu [Reference Mocanu23] where she improves the results in [Reference Işik, Kara and Ozman14] and proves similar versions for the Diophantine equation of signature
$x^p+y^q=z^r$
. The solutions of this equation have been studied over rationals by many mathematicians including Darmon, Merel, Bennett, and Poonen. Several mathematicians have worked on similar Fermat-type equations with different exponents over rational numbers. We have summarized these results in [Reference Işik, Kara and Ozman14]; therefore, we will not repeat them here, but we want to mention that not many results exist for generalizations of these to higher degree number fields. During the write-up of this paper, we have been informed about the work of Mocanu [Reference Mocanu23] where she improves the results in [Reference Işik, Kara and Ozman14] and proves similar versions for the Diophantine equation of signature
![]() $(p,p,3)$
. In this paper, we also study the solutions of
$(p,p,3)$
. In this paper, we also study the solutions of
![]() $x^p+y^p=z^3$
over number fields. However, our results differ from Mocanu (and hence the results in [Reference Işik, Kara and Ozman14]) in the sense that we prove results about solutions of equation (1.1) over fields that are not totally real. In the Appendix, we mention versions of these results for the Diophantine equation of signature
$x^p+y^p=z^3$
over number fields. However, our results differ from Mocanu (and hence the results in [Reference Işik, Kara and Ozman14]) in the sense that we prove results about solutions of equation (1.1) over fields that are not totally real. In the Appendix, we mention versions of these results for the Diophantine equation of signature
![]() $(p,p,2)$
. Our results can be summarized as follows.
$(p,p,2)$
. Our results can be summarized as follows.
1.1 Our results
Let K be a number field, and let
![]() ${\mathcal O}_{K}$
be its ring of integers. For a prime number p, we refer the equation
${\mathcal O}_{K}$
be its ring of integers. For a prime number p, we refer the equation
as the Fermat equation over K with signature (p,p,3). A solution
![]() $(a,b,c)$
is called trivial if
$(a,b,c)$
is called trivial if
![]() $abc=0$
, otherwise non-trivial. A solution
$abc=0$
, otherwise non-trivial. A solution
![]() $(a,b,c)$
of equation (1.1) is called primitive if
$(a,b,c)$
of equation (1.1) is called primitive if
![]() $a, b $
, and c are pairwise coprime. Since we will consider number fields with class number one, a putative solution
$a, b $
, and c are pairwise coprime. Since we will consider number fields with class number one, a putative solution
![]() $(a,b,c)$
can be scaled such that
$(a,b,c)$
can be scaled such that
![]() $a,b$
, and c are coprime.
$a,b$
, and c are coprime.
Note that if
![]() $p>3$
, then one can produce infinitely many nonprimitive solutions to equation (1.1). Indeed, if
$p>3$
, then one can produce infinitely many nonprimitive solutions to equation (1.1). Indeed, if
![]() $p\equiv -1\ \pmod {3}$
and
$p\equiv -1\ \pmod {3}$
and
![]() $a,b,c \in \mathcal {O}_K$
satisfying
$a,b,c \in \mathcal {O}_K$
satisfying
![]() $a^p+b^p=c$
, then
$a^p+b^p=c$
, then
![]() $(ac,bc,c^{\frac {p+1}{3}})$
is a nonprimitive solution to equation (1.1). Observe that if
$(ac,bc,c^{\frac {p+1}{3}})$
is a nonprimitive solution to equation (1.1). Observe that if
![]() $x,y,z \in \mathcal {O}_K$
satisfy
$x,y,z \in \mathcal {O}_K$
satisfy
![]() $x^p+y^p=z$
, then we have
$x^p+y^p=z$
, then we have
![]() $(xz)^p+(yz)^p=(z^{\frac {p+1}{2}})^2 $
, so one can obtain
$(xz)^p+(yz)^p=(z^{\frac {p+1}{2}})^2 $
, so one can obtain
![]() $a,b,c \in \mathcal {O}_K$
such that
$a,b,c \in \mathcal {O}_K$
such that
![]() $a^p+b^p=c^2$
. If
$a^p+b^p=c^2$
. If
![]() $p\equiv 1\ \pmod {3}$
and
$p\equiv 1\ \pmod {3}$
and
![]() $a,b,c \in \mathcal {O}_K$
such that
$a,b,c \in \mathcal {O}_K$
such that
![]() $a^p+b^p=c^2$
, then
$a^p+b^p=c^2$
, then
![]() $(ac,bc,c^{\frac {p+2}{3}})$
is a nonprimitive solution to equation (1.1). Thus, we consider only primitive solutions to equation (1.1). In [Reference Darmon and Granville5], it was shown that equation (1.1) has finitely many primitive solutions.
$(ac,bc,c^{\frac {p+2}{3}})$
is a nonprimitive solution to equation (1.1). Thus, we consider only primitive solutions to equation (1.1). In [Reference Darmon and Granville5], it was shown that equation (1.1) has finitely many primitive solutions.
We say that “the asymptotic Fermat Theorem holds for K and signature
![]() $(p,p,3)$
” if there is a constant
$(p,p,3)$
” if there is a constant
![]() $B_K$
such that, for any prime
$B_K$
such that, for any prime
![]() $p>B_K$
, the Fermat equation with signature
$p>B_K$
, the Fermat equation with signature
![]() $(p,p,3)$
(given in equation (1.1)) does not have nontrivial, primitive solutions.
$(p,p,3)$
(given in equation (1.1)) does not have nontrivial, primitive solutions.
We have two main results about solutions of equation (1.1). The first result is an asymptotic result for some of the solutions over general number fields, and the second one is an explicit result for general solutions over some imaginary quadratic fields.
Theorem 1.1 Let K be a number field with narrow class number
![]() $h_K^{+}=1$
satisfying Conjectures 2.2 and 2.3 and containing
$h_K^{+}=1$
satisfying Conjectures 2.2 and 2.3 and containing
![]() ${\mathbb Q}(\zeta _{3})$
where
${\mathbb Q}(\zeta _{3})$
where
![]() $\zeta _{3}$
is a primitive third root of unity. Assume that
$\zeta _{3}$
is a primitive third root of unity. Assume that
![]() $\lambda $
is the only prime of K lying above
$\lambda $
is the only prime of K lying above
![]() $3$
. Let
$3$
. Let
![]() $W_K$
be the set of
$W_K$
be the set of
![]() $(a,b,c)\in {\mathcal O}_K$
such that
$(a,b,c)\in {\mathcal O}_K$
such that
![]() $(a,b,c)$
is a primitive solution to
$(a,b,c)$
is a primitive solution to
![]() $x^p+y^p=z^3$
with
$x^p+y^p=z^3$
with
![]() $\lambda |b$
. Then there is a constant
$\lambda |b$
. Then there is a constant
![]() $B_K$
—depending only on K—such that, for
$B_K$
—depending only on K—such that, for
![]() $p> B_K$
, equation (
1.1
) has no solution
$p> B_K$
, equation (
1.1
) has no solution
![]() $(a,b,c) \in W_K$
. In this case, we say that the asymptotic FLT holds for
$(a,b,c) \in W_K$
. In this case, we say that the asymptotic FLT holds for
![]() $W_K$
and signature
$W_K$
and signature
![]() $(p,p,3)$
.
$(p,p,3)$
.
Theorem 1.2 Let
![]() $K={\mathbb Q}(\sqrt {-d})$
, where
$K={\mathbb Q}(\sqrt {-d})$
, where
![]() $d\in \{1,7,19,43,67\}$
, and let
$d\in \{1,7,19,43,67\}$
, and let
![]() $\ell _K$
be the largest prime in Table 2 corresponding to K. Let
$\ell _K$
be the largest prime in Table 2 corresponding to K. Let
![]() $C_K, M_K$
be defined as in Proposition 3.9 and Corollary 3.10. Assume that Conjecture 2.2 holds true for K. Let
$C_K, M_K$
be defined as in Proposition 3.9 and Corollary 3.10. Assume that Conjecture 2.2 holds true for K. Let
![]() $\lambda $
be the prime of
$\lambda $
be the prime of
![]() ${\mathcal O}_K$
lying over
${\mathcal O}_K$
lying over
![]() $3$
. Then:
$3$
. Then:
-
Case I For any prime
 $p> \mathrm {max} \{\ell _K, C_K\}$
, the Fermat equation over K with signature
$p> \mathrm {max} \{\ell _K, C_K\}$
, the Fermat equation over K with signature
 $(p,p,3)$
does not have any nontrivial primitive solutions
$(p,p,3)$
does not have any nontrivial primitive solutions
 $(a,b,c)\in {\mathcal O}_{K}$
such that
$(a,b,c)\in {\mathcal O}_{K}$
such that
 $\lambda | b$
.
$\lambda | b$
. -
Case II If
 $p> B_K=\mathrm {max}\{\ell _K,C_K,M_K\}$
, p splits in K, and
$p> B_K=\mathrm {max}\{\ell _K,C_K,M_K\}$
, p splits in K, and
 $p \equiv 3\ \pmod 4$
, then the Fermat equation over K with signature
$p \equiv 3\ \pmod 4$
, then the Fermat equation over K with signature
 $(p,p,3)$
does not have any nontrivial primitive solutions
$(p,p,3)$
does not have any nontrivial primitive solutions
 $(a,b,c)\in {\mathcal O}_{K}$
.
$(a,b,c)\in {\mathcal O}_{K}$
.
Table 1: Numerical examples.

Table 2: Prime torsions in
![]() $\Gamma _0({\mathfrak N}_E)^{\mathrm {ab}}.$
$\Gamma _0({\mathfrak N}_E)^{\mathrm {ab}}.$

Remark 1.3 The bound for Case 1 above is
![]() $199$
, and this bound can be made smaller depending on the field we work on, as can be seen in Table 2. Combining this with Proposition 3.9 and Case 1 of Corollary 3.10, we see that the bound
$199$
, and this bound can be made smaller depending on the field we work on, as can be seen in Table 2. Combining this with Proposition 3.9 and Case 1 of Corollary 3.10, we see that the bound
![]() $199$
works for all the five imaginary quadratic fields mentioned in the statement of Theorem 1.2.
$199$
works for all the five imaginary quadratic fields mentioned in the statement of Theorem 1.2.
Similarly, for Case 2 of Theorem 1.2, it is possible to take
![]() $B_K$
as
$B_K$
as
![]() $44,483$
, using Proposition 3.9 and Case 2(a) of Corollary 3.10.
$44,483$
, using Proposition 3.9 and Case 2(a) of Corollary 3.10.
Various different techniques have to be combined to achieve these results. For the asymptotic result, we mostly follow the approach in [Reference Işik, Kara and Ozman14, Reference Kara and Ozman17], which relies on the paper of Şengün and Siksek [Reference Şengün and Siksek27]. For instance, we need the absolute irreducibility of the associated Galois representation in order to apply the Serre’s modularity conjecture. In order to do this, one needs to prove the irreducibility first and then pass to absolute irreducibility. This is rather classical when the Frey curve has potentially multiplicative reduction at q for some q appearing in the denominator of the j-invariant of the Frey curve. However, for
![]() $(p,p,3)$
case, the associated Frey elliptic curve has potentially good reduction when
$(p,p,3)$
case, the associated Frey elliptic curve has potentially good reduction when
![]() $3$
does not divide the norm of
$3$
does not divide the norm of
![]() $ab$
. Therefore, one can only get a result about solutions of a particular type. This was also mentioned in the papers of Turcas [Reference Ţurcaş31, Reference Ţurcaş32]. It is sometimes possible to overcome this obstruction when working over explicit fields. For instance, as done by Najman and Turcas in [Reference Najman and Ţurcaş24], using a result of Vaintrob and Larson, it is possible to prove the absolute irreducibility of the associated Galois representation when p is bigger than a computable constant
$ab$
. Therefore, one can only get a result about solutions of a particular type. This was also mentioned in the papers of Turcas [Reference Ţurcaş31, Reference Ţurcaş32]. It is sometimes possible to overcome this obstruction when working over explicit fields. For instance, as done by Najman and Turcas in [Reference Najman and Ţurcaş24], using a result of Vaintrob and Larson, it is possible to prove the absolute irreducibility of the associated Galois representation when p is bigger than a computable constant
![]() $B_K$
. One can apply a similar argument to the Galois representation related to the Diophantine equation of signature
$B_K$
. One can apply a similar argument to the Galois representation related to the Diophantine equation of signature
![]() $(p,p,3)$
. Of course, in order to do this, we need an irreducibility result for
$(p,p,3)$
. Of course, in order to do this, we need an irreducibility result for
![]() $\overline {\rho }_{E,p}$
when p is bigger than an explicit constant B. This is a nontrivial task to do even in the case of the classical Fermat equation, which was done by Freitas and Siksek in [Reference Freitas and Siksek13]. We combine all these to obtain our second result, which gives information about the solutions of
$\overline {\rho }_{E,p}$
when p is bigger than an explicit constant B. This is a nontrivial task to do even in the case of the classical Fermat equation, which was done by Freitas and Siksek in [Reference Freitas and Siksek13]. We combine all these to obtain our second result, which gives information about the solutions of
![]() $(p,p,3)$
over imaginary quadratic number fields of class number one.
$(p,p,3)$
over imaginary quadratic number fields of class number one.
2 Preliminaries
In this section we give the necessary background to prove the results. We follow [Reference Freitas and Siksek12, Reference Şengün and Siksek27] and the references therein.
2.1 Conjectures
In this subsection, we state the conjectures assumed in the above theorems. For more details, we refer to Sections 2 and 3 of [Reference Şengün and Siksek27].
Let K be a number field with the ring of integers
![]() ${\mathcal O}_{K}$
, and let
${\mathcal O}_{K}$
, and let
![]() ${\mathfrak N}$
be an ideal of
${\mathfrak N}$
be an ideal of
![]() ${\mathcal O}_{K}$
. The following result is proved by Şengün and Siksek in [Reference Şengün and Siksek27].
${\mathcal O}_{K}$
. The following result is proved by Şengün and Siksek in [Reference Şengün and Siksek27].
Proposition 2.1 [Reference Şengün and Siksek27, Proposition 2.1]
There is an integer
![]() $B({\mathfrak N})$
, depending only on
$B({\mathfrak N})$
, depending only on
![]() ${\mathfrak N}$
, such that, for any prime
${\mathfrak N}$
, such that, for any prime
![]() $p>B({\mathfrak N})$
, every weight-two, mod p eigenform of level
$p>B({\mathfrak N})$
, every weight-two, mod p eigenform of level
![]() ${\mathfrak N}$
lifts to a complex one.
${\mathfrak N}$
lifts to a complex one.
In order to run the modular approach to solve Diophantine equations, one needs generalized modularity theorems. Due to the lack of their existence, we can only prove our theorems up to some conjectures. One of the assumed conjectures is a special case of Serre’s modularity conjecture over number fields, stated below.
Conjecture 2.2 [Reference Freitas, Kraus and Siksek11, Conjecture 4.1]
Let
![]() $\overline {\rho }:G_K\rightarrow GL_2(\overline {\mathbb {F}}_p)$
be an odd, irreducible, continuous representation with Serre conductor
$\overline {\rho }:G_K\rightarrow GL_2(\overline {\mathbb {F}}_p)$
be an odd, irreducible, continuous representation with Serre conductor
![]() ${\mathfrak N}$
(prime-to-p part of its Artin conductor) such that
${\mathfrak N}$
(prime-to-p part of its Artin conductor) such that
![]() $\det (\overline {\rho })=\chi _p$
is the mod p cyclotomic character. Assume that p is unramified in K and that
$\det (\overline {\rho })=\chi _p$
is the mod p cyclotomic character. Assume that p is unramified in K and that
![]() $\overline {\rho }|_{G_{K_{{\mathfrak p}}}}$
arises from a finite-flat group scheme over
$\overline {\rho }|_{G_{K_{{\mathfrak p}}}}$
arises from a finite-flat group scheme over
![]() ${\mathcal O}_{K_{{\mathfrak p}}}$
for every prime
${\mathcal O}_{K_{{\mathfrak p}}}$
for every prime
![]() ${\mathfrak p}|p$
. Then there is a weight-two, mod p eigenform
${\mathfrak p}|p$
. Then there is a weight-two, mod p eigenform
![]() $\theta $
over K of level
$\theta $
over K of level
![]() ${\mathfrak N}$
such that, for all primes
${\mathfrak N}$
such that, for all primes
![]() ${\mathfrak q}$
coprime to
${\mathfrak q}$
coprime to
![]() $p{\mathfrak N}$
, we have
$p{\mathfrak N}$
, we have
where
![]() $T_{{\mathfrak q}}$
denotes the Hecke operator at
$T_{{\mathfrak q}}$
denotes the Hecke operator at
![]() ${\mathfrak q}$
.
${\mathfrak q}$
.
Additionally, we will use a special case of a fundamental conjecture from the Langlands program for the asymptotic result. Note that we do not need Conjecture 2.3 for Theorem 1.2 since K is restricted to a finite (fixed) list of fields.
Conjecture 2.3 [Reference Şengün and Siksek27, Conjecture 4.1]
Let
![]() ${\mathfrak f}$
be a weight-two complex eigenform over K of level
${\mathfrak f}$
be a weight-two complex eigenform over K of level
![]() ${\mathfrak N}$
that is nontrivial and new. If K has some real place, then there exists an elliptic curve
${\mathfrak N}$
that is nontrivial and new. If K has some real place, then there exists an elliptic curve
![]() $E_{{\mathfrak f}}/K$
of conductor
$E_{{\mathfrak f}}/K$
of conductor
![]() ${\mathfrak N}$
such that
${\mathfrak N}$
such that
If K is totally complex, then there exists either an elliptic curve
![]() $E_{{\mathfrak f}}$
of conductor
$E_{{\mathfrak f}}$
of conductor
![]() ${\mathfrak N}$
satisfying (2.1) or a fake elliptic curve
${\mathfrak N}$
satisfying (2.1) or a fake elliptic curve
![]() $A_{{\mathfrak f}}/K$
, of conductor
$A_{{\mathfrak f}}/K$
, of conductor
![]() ${\mathfrak N}^2$
, such that
${\mathfrak N}^2$
, such that
2.2 Frey curve and related facts
In this subsection, we collect some facts related to the Frey curve associated with a putative solution of equation (1.1) and the associated Galois representation.
Let
![]() $G_{K} $
be the absolute Galois group of a number field K, let
$G_{K} $
be the absolute Galois group of a number field K, let
![]() $E/K$
be an elliptic curve, and let
$E/K$
be an elliptic curve, and let
![]() $ \overline {\rho }_{E,p}$
denote the mod p Galois representation of E. We use
$ \overline {\rho }_{E,p}$
denote the mod p Galois representation of E. We use
![]() ${\mathfrak q}$
for an arbitrary prime of K, and
${\mathfrak q}$
for an arbitrary prime of K, and
![]() $G_{\mathfrak q}$
and
$G_{\mathfrak q}$
and
![]() $I_{\mathfrak q}$
, respectively, for the decomposition and inertia subgroups of
$I_{\mathfrak q}$
, respectively, for the decomposition and inertia subgroups of
![]() $G_K$
at
$G_K$
at
![]() ${\mathfrak q}$
. For a putative solution
${\mathfrak q}$
. For a putative solution
![]() $(a,b,c)$
to equation (1.1) with a prime exponent p, we associate the Frey elliptic curve as in [Reference Bennett, Vatsal and Yazdani2],
$(a,b,c)$
to equation (1.1) with a prime exponent p, we associate the Frey elliptic curve as in [Reference Bennett, Vatsal and Yazdani2],
whose arithmetic invariants are given by
![]() $\Delta _E=3^3(ab^3)^p$
,
$\Delta _E=3^3(ab^3)^p$
,
 $\displaystyle j_E=\frac {3^3c^3(9a^p+b^p)^3}{(ab^3)^p}$
, and
$\displaystyle j_E=\frac {3^3c^3(9a^p+b^p)^3}{(ab^3)^p}$
, and
![]() $c_4(E)=9c(9a^p+b^p), c_6(E)=-3^3(3^3c^6-2^23^2c^3b^p+2^3b^{2p})$
.
$c_4(E)=9c(9a^p+b^p), c_6(E)=-3^3(3^3c^6-2^23^2c^3b^p+2^3b^{2p})$
.
For the result below, we have the same assumptions on the number field K mentioned in the introduction. Namely, K is a number field of degree d such that the narrow class number of K,
![]() $h_K^{+}=1$
and there is a unique prime
$h_K^{+}=1$
and there is a unique prime
![]() $\lambda $
over
$\lambda $
over
![]() $3$
.
$3$
.
Lemma 2.4 Let
![]() $\lambda ^e=3 \mathcal {O}_K$
where
$\lambda ^e=3 \mathcal {O}_K$
where
![]() $\mathcal {O}_K$
is the integer ring of K. The Frey curve E is semistable away from
$\mathcal {O}_K$
is the integer ring of K. The Frey curve E is semistable away from
![]() $\lambda $
and has a K-rational point of order
$\lambda $
and has a K-rational point of order
![]() $3$
. The determinant of
$3$
. The determinant of
![]() $\overline {\rho }_{E,p}$
is the mod p cyclotomic character. The Galois representation
$\overline {\rho }_{E,p}$
is the mod p cyclotomic character. The Galois representation
![]() $\overline {\rho }_{E,p}$
is finite flat at every prime
$\overline {\rho }_{E,p}$
is finite flat at every prime
![]() ${\mathfrak p}$
of K that lies above p. Moreover, the conductor
${\mathfrak p}$
of K that lies above p. Moreover, the conductor
![]() $\mathcal {N}_E$
attached to the Frey curve E is given by
$\mathcal {N}_E$
attached to the Frey curve E is given by
where
-
(1)
 $\epsilon \in \{0,1\}$
if
$\epsilon \in \{0,1\}$
if
 $\lambda | ab$
and
$\lambda | ab$
and
 $p> 2e$
.
$p> 2e$
. -
(2)
 $\epsilon \geq 2,3$
if
$\epsilon \geq 2,3$
if
 $\lambda \nmid ab$
. Moreover, if
$\lambda \nmid ab$
. Moreover, if
 $e=1$
,
$e=1$
,
 $\epsilon \in \{2,3\}.$
$\epsilon \in \{2,3\}.$
In particular, if
![]() $\lambda | ab$
, the curve E is semistable, and otherwise, the curve E has additive reduction at
$\lambda | ab$
, the curve E is semistable, and otherwise, the curve E has additive reduction at
![]() $\lambda $
.
$\lambda $
.
The Serre conductor
![]() ${\mathfrak N}_E$
, which is the prime-to-p part of the Artin conductor of
${\mathfrak N}_E$
, which is the prime-to-p part of the Artin conductor of
![]() $\overline {\rho }_{E,p}$
, is supported on
$\overline {\rho }_{E,p}$
, is supported on
![]() $\lambda $
and belongs to a finite set depending only on the field K.
$\lambda $
and belongs to a finite set depending only on the field K.
Proof Assume that the narrow class number
![]() $h_K^{+}=1$
. Recall that the invariants
$h_K^{+}=1$
. Recall that the invariants
![]() $c_4(E), c_6(E)$
, and
$c_4(E), c_6(E)$
, and
![]() $\Delta _E$
of the model E are given by
$\Delta _E$
of the model E are given by
Suppose that
![]() ${\mathfrak q} \neq \lambda $
divides
${\mathfrak q} \neq \lambda $
divides
![]() $\Delta _E$
, which implies that
$\Delta _E$
, which implies that
![]() $ab$
is divisible by
$ab$
is divisible by
![]() ${\mathfrak q}$
. Since
${\mathfrak q}$
. Since
![]() $a,b$
, and c are pairwise coprime,
$a,b$
, and c are pairwise coprime,
![]() ${\mathfrak q}$
divides either a or b. Therefore,
${\mathfrak q}$
divides either a or b. Therefore,
![]() $c_4(E)= 9c(9a^p+b^p)$
is not divisible by
$c_4(E)= 9c(9a^p+b^p)$
is not divisible by
![]() ${\mathfrak q}$
, i.e.,
${\mathfrak q}$
, i.e.,
![]() $v_{{\mathfrak q}}(c_4(E))=0$
. Hence, the given model is minimal and E is semistable at
$v_{{\mathfrak q}}(c_4(E))=0$
. Hence, the given model is minimal and E is semistable at
![]() ${\mathfrak q}$
. Moreover, we have
${\mathfrak q}$
. Moreover, we have
![]() $p|v_{{\mathfrak q}}(\Delta _E)$
. It follows from [Reference Serre28] that
$p|v_{{\mathfrak q}}(\Delta _E)$
. It follows from [Reference Serre28] that
![]() $\overline {\rho }_{E,p}$
is finite flat at
$\overline {\rho }_{E,p}$
is finite flat at
![]() ${\mathfrak q}$
if
${\mathfrak q}$
if
![]() ${\mathfrak q}$
lies above p. We can also deduce that
${\mathfrak q}$
lies above p. We can also deduce that
![]() $\overline {\rho }_{E,p}$
is unramified at
$\overline {\rho }_{E,p}$
is unramified at
![]() ${\mathfrak q}$
if
${\mathfrak q}$
if
![]() ${\mathfrak q} \nmid p$
.
${\mathfrak q} \nmid p$
.
Now, assume that
![]() $\lambda $
divides
$\lambda $
divides
![]() $ab$
. Note that
$ab$
. Note that
![]() $\lambda $
can only divide one of a or b. Without loss of generality, say
$\lambda $
can only divide one of a or b. Without loss of generality, say
![]() $\lambda | b$
. The result regarding
$\lambda | b$
. The result regarding
![]() $\lambda \nmid ab$
can be handled in an identical manner.
$\lambda \nmid ab$
can be handled in an identical manner.
In all cases, the valuation
![]() $v_\lambda (\mathcal {N}_E)=\epsilon $
can be calculated via [Reference Papadopoulos25, Tableau III]. Note that, when
$v_\lambda (\mathcal {N}_E)=\epsilon $
can be calculated via [Reference Papadopoulos25, Tableau III]. Note that, when
![]() $\lambda | ab$
, the equation is not minimal. After using the change of variables
$\lambda | ab$
, the equation is not minimal. After using the change of variables
![]() $X=3^2x, Y=3^3y$
, we get
$X=3^2x, Y=3^3y$
, we get
![]() $v_\lambda (c_4(E))=v_\lambda (c_6(E))=0$
when
$v_\lambda (c_4(E))=v_\lambda (c_6(E))=0$
when
![]() $p> 2e$
, and hence
$p> 2e$
, and hence
![]() $\epsilon =0,1.$
$\epsilon =0,1.$
The statement concerning the determinant is a well-known consequence of the Weil pairing attached to elliptic curves. The fact that the Frey curve E has a K-rational point of order
![]() $3$
follows from [Reference Bennett, Vatsal and Yazdani2, Lemma 2.1(c)].
$3$
follows from [Reference Bennett, Vatsal and Yazdani2, Lemma 2.1(c)].
Finally, to show that there can be only finitely many Serre conductors
![]() ${\mathfrak N}_E$
, note that only the prime
${\mathfrak N}_E$
, note that only the prime
![]() $\lambda $
can divide
$\lambda $
can divide
![]() ${\mathfrak N}_E$
. As
${\mathfrak N}_E$
. As
![]() ${\mathfrak N}_E$
divides the conductor
${\mathfrak N}_E$
divides the conductor
![]() ${\mathcal N}_E$
of E,
${\mathcal N}_E$
of E,
![]() $v_{\lambda }({\mathfrak N}_E)\leq v_{\lambda }({\mathcal N}_E)\leq 2+3 v_{\lambda }(3)+6 v_{\lambda }(2)$
by [Reference Silverman29, Theorem IV.10.4]. Hence, there can be only finitely many Serre conductors and they only depend on K.
$v_{\lambda }({\mathfrak N}_E)\leq v_{\lambda }({\mathcal N}_E)\leq 2+3 v_{\lambda }(3)+6 v_{\lambda }(2)$
by [Reference Silverman29, Theorem IV.10.4]. Hence, there can be only finitely many Serre conductors and they only depend on K.
Given a number field K, we obtain a complex conjugation for every real embedding
![]() $\sigma : K \hookrightarrow \mathbb R$
and every extension
$\sigma : K \hookrightarrow \mathbb R$
and every extension
![]() $\tilde {\sigma }: \overline {K} \hookrightarrow \mathbb C$
of
$\tilde {\sigma }: \overline {K} \hookrightarrow \mathbb C$
of
![]() $\sigma $
as
$\sigma $
as
![]() $\tilde {\sigma }^{-1}\iota \tilde {\sigma } \in G_K$
where
$\tilde {\sigma }^{-1}\iota \tilde {\sigma } \in G_K$
where
![]() $\iota $
is the usual complex conjugation. Recall that a representation
$\iota $
is the usual complex conjugation. Recall that a representation
![]() $\overline {\rho }_{E,p}: G_K \rightarrow \operatorname {\mathrm {GL}}_2(\overline {\mathbb F}_p)$
is odd if the determinant of every complex conjugation is
$\overline {\rho }_{E,p}: G_K \rightarrow \operatorname {\mathrm {GL}}_2(\overline {\mathbb F}_p)$
is odd if the determinant of every complex conjugation is
![]() $-1$
. If the number field K has no real embeddings, then we immediately say that
$-1$
. If the number field K has no real embeddings, then we immediately say that
![]() $\overline {\rho }_{E,p}$
is odd.
$\overline {\rho }_{E,p}$
is odd.
The following results give us information about the image of inertia groups under the Galois representation
![]() $\overline {\rho }_{E,p}$
.
$\overline {\rho }_{E,p}$
.
Lemma 2.5 [Reference Freitas and Siksek12, Lemma 3.4]
Let E be an elliptic curve over K with j-invariant
![]() $j_E$
. Let
$j_E$
. Let
![]() $p \geq 5$
, and let
$p \geq 5$
, and let
![]() $\mathfrak {q}\nmid p$
be a prime of K. Then
$\mathfrak {q}\nmid p$
be a prime of K. Then
![]() $p|\#\overline {\rho }_{E,p}(I_{\mathfrak {q}})$
if and only if E has potentially multiplicative reduction at
$p|\#\overline {\rho }_{E,p}(I_{\mathfrak {q}})$
if and only if E has potentially multiplicative reduction at
![]() $\mathfrak {q}$
(i.e.,
$\mathfrak {q}$
(i.e.,
![]() $\upsilon _{\mathfrak {q}}(j_E)<0$
) and
$\upsilon _{\mathfrak {q}}(j_E)<0$
) and
![]() $p \nmid \upsilon _{\mathfrak {q}}(j_E)$
.
$p \nmid \upsilon _{\mathfrak {q}}(j_E)$
.
By using the previous result, we obtain the following lemma.
Lemma 2.6 Let
![]() $\lambda $
be the only prime ideal of K lying above
$\lambda $
be the only prime ideal of K lying above
![]() $3$
, and let
$3$
, and let
![]() $(a,b,c)\in W_K$
with prime exponent
$(a,b,c)\in W_K$
with prime exponent
![]() $p>\upsilon _{\lambda }(3)$
. Let E be the Frey curve as in (
2.3
), and write
$p>\upsilon _{\lambda }(3)$
. Let E be the Frey curve as in (
2.3
), and write
![]() $j_E$
for its j-invariant. Then E has potentially multiplicative reduction at
$j_E$
for its j-invariant. Then E has potentially multiplicative reduction at
![]() $\lambda $
and
$\lambda $
and
![]() $p|\#\overline {\rho }_{E,p}(I_{\lambda })$
where
$p|\#\overline {\rho }_{E,p}(I_{\lambda })$
where
![]() $I_{\lambda }$
denotes an inertia subgroup of
$I_{\lambda }$
denotes an inertia subgroup of
![]() $G_{K}$
at
$G_{K}$
at
![]() $\lambda $
.
$\lambda $
.
Proof Assume that
![]() $\lambda $
is the only prime ideal of K lying above
$\lambda $
is the only prime ideal of K lying above
![]() $3$
with
$3$
with
![]() $\upsilon _{\lambda }(b)=k$
. Then
$\upsilon _{\lambda }(b)=k$
. Then
![]() $\upsilon _{\lambda }(j_E)=3\upsilon _{\lambda }(3)-3pk$
. Since
$\upsilon _{\lambda }(j_E)=3\upsilon _{\lambda }(3)-3pk$
. Since
![]() $p>\upsilon _{\lambda }(3)$
, and
$p>\upsilon _{\lambda }(3)$
, and
![]() $k \geq 1$
, we have
$k \geq 1$
, we have
![]() $v_{\lambda }(j_E)<0$
and clearly
$v_{\lambda }(j_E)<0$
and clearly
![]() $p \nmid \upsilon _{\lambda }(j_E)$
. This implies that E has potentially multiplicative reduction at
$p \nmid \upsilon _{\lambda }(j_E)$
. This implies that E has potentially multiplicative reduction at
![]() $\lambda $
and
$\lambda $
and
![]() $p| \#\overline {\rho }_{E,p}(I_{\lambda })$
.
$p| \#\overline {\rho }_{E,p}(I_{\lambda })$
.
The following well-known result about subgroups of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb F_p)$
will be frequently used.
$\operatorname {\mathrm {GL}}_2(\mathbb F_p)$
will be frequently used.
Theorem 2.7 Let E be an elliptic curve over a number field K of degree d, and let
![]() $G \leq \operatorname {\mathrm {GL}}_2(\mathbb F_p)$
be the image of the mod p Galois representation of E. Then the following holds:
$G \leq \operatorname {\mathrm {GL}}_2(\mathbb F_p)$
be the image of the mod p Galois representation of E. Then the following holds:
-
• If
 $p | \#G$
, then either G is reducible or G contains
$p | \#G$
, then either G is reducible or G contains
 $\operatorname {\mathrm {SL}}_2(\mathbb F_p)$
, and hence it is absolutely irreducible.
$\operatorname {\mathrm {SL}}_2(\mathbb F_p)$
, and hence it is absolutely irreducible. -
• If
 $p \nmid \#G$
and
$p \nmid \#G$
and
 $p> 15 d +1$
, then G is contained in a Cartan subgroup or G is contained in the normalizer of Cartan subgroup but not the Cartan subgroup itself.
$p> 15 d +1$
, then G is contained in a Cartan subgroup or G is contained in the normalizer of Cartan subgroup but not the Cartan subgroup itself.
Proof For the proof, the main reference is [Reference Swinnerton-Dyer30, Lemma 2]. The version above including the proof of the second part is from [Reference Etropolski10, Propositions 2.3 and 2.6].
3 Properties of Galois representations
3.1 Level reduction
In this subsection, we will be relating the Galois representation attached to the Frey curve with another representation of lower level.
Theorem 3.1 Let K be a number field with
![]() $h^{+}_K=1$
satisfying Conjectures 2.2 and 2.3. Assume that
$h^{+}_K=1$
satisfying Conjectures 2.2 and 2.3. Assume that
![]() $\lambda $
is the only prime of K above
$\lambda $
is the only prime of K above
![]() $3$
. Then there is a constant
$3$
. Then there is a constant
![]() $B_K$
depending only on K such that the following holds. Let
$B_K$
depending only on K such that the following holds. Let
![]() $(a,b,c)\in W_K$
be a nontrivial solution to equation (
1.1
) with exponent
$(a,b,c)\in W_K$
be a nontrivial solution to equation (
1.1
) with exponent
![]() $p>B_K$
. Let
$p>B_K$
. Let
![]() $E/K$
be the associated Frey curve defined in (2.3). Then there is an elliptic curve
$E/K$
be the associated Frey curve defined in (2.3). Then there is an elliptic curve
![]() $E'/K$
such that the following statements hold:
$E'/K$
such that the following statements hold:
-
(1)
 $E'$
has good reduction away from
$E'$
has good reduction away from
 $\lambda $
.
$\lambda $
. -
(2)
 $E'$
has a K-rational point of order
$E'$
has a K-rational point of order
 $3$
.
$3$
. -
(3)
 $\overline {\rho }_{E,p}\sim \overline {\rho }_{E',p}$
.
$\overline {\rho }_{E,p}\sim \overline {\rho }_{E',p}$
. -
(4)
 $v_{\lambda }(j')<0$
where
$v_{\lambda }(j')<0$
where
 $j'$
is the j-invariant of
$j'$
is the j-invariant of
 $E'$
.
$E'$
.
We will give the proof of this theorem in Section 3.1.1 after stating the necessary lemmas. The following is Proposition 6.1 of [Reference Şengün and Siksek27]. We include its statement for the convenience of the reader, but we will omit its proof and refer to [Reference Şengün and Siksek27] instead.
Proposition 3.2 Let L be a Galois number field, and let
![]() ${\mathfrak q}$
be a prime of L. There is a constant
${\mathfrak q}$
be a prime of L. There is a constant
![]() $B_{L,{\mathfrak q}}$
such that the following is true. Let
$B_{L,{\mathfrak q}}$
such that the following is true. Let
![]() $p> B_{L, {\mathfrak q}}$
be a rational prime. Let
$p> B_{L, {\mathfrak q}}$
be a rational prime. Let
![]() $E/L$
be an elliptic curve that is semistable at all
$E/L$
be an elliptic curve that is semistable at all
![]() ${\mathfrak p} | p$
and having potentially multiplicative reduction at
${\mathfrak p} | p$
and having potentially multiplicative reduction at
![]() ${\mathfrak q}$
. Then
${\mathfrak q}$
. Then
![]() $\overline {\rho }_{E,p}$
is irreducible.
$\overline {\rho }_{E,p}$
is irreducible.
By applying the above proposition to the Frey curve, we get the following corollary.
Corollary 3.3 Let K be a number field with
![]() $h^{+}_K=1$
, and suppose that
$h^{+}_K=1$
, and suppose that
![]() $\lambda $
is the only prime of K above
$\lambda $
is the only prime of K above
![]() $3$
. There is a constant
$3$
. There is a constant
![]() $C_K$
such that if
$C_K$
such that if
![]() $p>C_K$
and
$p>C_K$
and
![]() $(a,b,c)\in W_K$
is a nontrivial solution to the Fermat equation with signature
$(a,b,c)\in W_K$
is a nontrivial solution to the Fermat equation with signature
![]() $(p,p,3)$
, then
$(p,p,3)$
, then
![]() $\overline {\rho }_{E,p}$
is surjective, where E is the Frey curve given in (
2.3
).
$\overline {\rho }_{E,p}$
is surjective, where E is the Frey curve given in (
2.3
).
Proof By Lemma 2.6, E has potentially multiplicative reduction at
![]() $\lambda $
. Moreover, E is semistable away from
$\lambda $
. Moreover, E is semistable away from
![]() $\lambda $
from Lemma 2.4. Let L be the Galois closure of K, and let
$\lambda $
from Lemma 2.4. Let L be the Galois closure of K, and let
![]() ${\mathfrak q}$
be a prime of L above
${\mathfrak q}$
be a prime of L above
![]() $\lambda $
. Now, by applying Proposition 3.2, we get a constant
$\lambda $
. Now, by applying Proposition 3.2, we get a constant
![]() $B_{L,{\mathfrak q}}$
such that
$B_{L,{\mathfrak q}}$
such that
![]() $\overline {\rho }_{E,p}(G_L)$
is irreducible whenever
$\overline {\rho }_{E,p}(G_L)$
is irreducible whenever
![]() $p>B_{L,{\mathfrak q}}$
. Note that there are only finitely many choices of
$p>B_{L,{\mathfrak q}}$
. Note that there are only finitely many choices of
![]() ${\mathfrak q}|3$
in L and L only depends on K. Hence, we can obtain a constant depending only on K and we denote it by
${\mathfrak q}|3$
in L and L only depends on K. Hence, we can obtain a constant depending only on K and we denote it by
![]() $C_K$
. If necessary, enlarge
$C_K$
. If necessary, enlarge
![]() $C_{K}$
so that
$C_{K}$
so that
![]() $C_{K}>v_{\lambda }(3)$
. Now, we apply Lemma 2.6 and see that the image of
$C_{K}>v_{\lambda }(3)$
. Now, we apply Lemma 2.6 and see that the image of
![]() $\overline {\rho }_{E,p}$
contains an element of order p. By Theorem 2.7, any subgroup of
$\overline {\rho }_{E,p}$
contains an element of order p. By Theorem 2.7, any subgroup of
![]() $\operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
having an element of order p is either reducible or contains
$\operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
having an element of order p is either reducible or contains
![]() $\operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
. As
$\operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
. As
![]() $p>C_K>v_{\lambda }(3)$
, the image contains
$p>C_K>v_{\lambda }(3)$
, the image contains
![]() $\operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
. Finally, we can ensure that
$\operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
. Finally, we can ensure that
![]() $K\cap {\mathbb Q}(\zeta _p)={\mathbb Q}$
by taking
$K\cap {\mathbb Q}(\zeta _p)={\mathbb Q}$
by taking
![]() $C_K$
large enough if needed. Hence,
$C_K$
large enough if needed. Hence,
![]() $\chi _p=\det (\overline {\rho }_{E,p})$
is surjective.
$\chi _p=\det (\overline {\rho }_{E,p})$
is surjective.
3.1.1 Proof of Theorem 3.1
In this subsection, Theorem 3.1 will be proved. Although the proof closely follows the ideas in [Reference Kara and Ozman17], we will give it here for the sake of completeness and for the convenience of the reader. We continue with the notations introduced in the statement of Theorem 3.1 and the assumptions of the theorem.
Lemma 3.4 There is a nontrivial, new (weight-two) complex eigenform
![]() ${\mathfrak f}$
which has an associated elliptic curve
${\mathfrak f}$
which has an associated elliptic curve
![]() $E_{{\mathfrak f}}/K$
of conductor
$E_{{\mathfrak f}}/K$
of conductor
![]() ${\mathfrak N}'$
dividing
${\mathfrak N}'$
dividing
![]() ${\mathfrak N}_E$
.
${\mathfrak N}_E$
.
Proof We first show the existence of such an eigenform
![]() ${\mathfrak f}$
of level
${\mathfrak f}$
of level
![]() ${\mathfrak N}_E$
supported only on
${\mathfrak N}_E$
supported only on
![]() $\{\lambda \}$
.
$\{\lambda \}$
.
By Corollary 3.3, the representation
![]() $\overline {\rho }_{E,p}:G_K\rightarrow GL_{2}(\mathbb {F}_p) $
is surjective and hence is absolutely irreducible for
$\overline {\rho }_{E,p}:G_K\rightarrow GL_{2}(\mathbb {F}_p) $
is surjective and hence is absolutely irreducible for
![]() $p>C_K$
. Now, we apply Conjecture 2.2 to deduce that there is a weight-two, mod p eigenform
$p>C_K$
. Now, we apply Conjecture 2.2 to deduce that there is a weight-two, mod p eigenform
![]() $\theta $
over K of level
$\theta $
over K of level
![]() ${\mathfrak N}_E$
, with
${\mathfrak N}_E$
, with
![]() ${\mathfrak N}_E$
as in Lemma 2.4, such that, for all primes
${\mathfrak N}_E$
as in Lemma 2.4, such that, for all primes
![]() ${\mathfrak q}$
coprime to
${\mathfrak q}$
coprime to
![]() $p{\mathfrak N}$
, we have
$p{\mathfrak N}$
, we have
We also know from the same lemma that there are only finitely many possible levels
![]() ${\mathfrak N}$
. Thus, by taking p large enough (see Proposition 2.1) for any level
${\mathfrak N}$
. Thus, by taking p large enough (see Proposition 2.1) for any level
![]() ${\mathfrak N}$
, there is a weight-two complex eigenform
${\mathfrak N}$
, there is a weight-two complex eigenform
![]() ${\mathfrak f}$
with level
${\mathfrak f}$
with level
![]() ${\mathfrak N}$
which is a lift of
${\mathfrak N}$
which is a lift of
![]() $\theta $
. Note that since there are only finitely many such eigenforms
$\theta $
. Note that since there are only finitely many such eigenforms
![]() ${\mathfrak f}$
and they depend only on K, from now on, we can suppose that every constant depending on these eigenforms depends only on K.
${\mathfrak f}$
and they depend only on K, from now on, we can suppose that every constant depending on these eigenforms depends only on K.
Next, we recall that if
![]() ${\mathbb Q}_{{\mathfrak f}}\neq {\mathbb Q}$
, then there is a constant
${\mathbb Q}_{{\mathfrak f}}\neq {\mathbb Q}$
, then there is a constant
![]() $C_{{\mathfrak f}}$
depending only on
$C_{{\mathfrak f}}$
depending only on
![]() ${\mathfrak f}$
such that
${\mathfrak f}$
such that
![]() $p<C_{{\mathfrak f}}$
[Reference Şengün and Siksek27, Lemma 7.2]. Therefore, by taking p sufficiently large, we assume that
$p<C_{{\mathfrak f}}$
[Reference Şengün and Siksek27, Lemma 7.2]. Therefore, by taking p sufficiently large, we assume that
![]() ${\mathbb Q}_{{\mathfrak f}}={\mathbb Q}$
. In order to apply Conjecture 2.3, we need to show that
${\mathbb Q}_{{\mathfrak f}}={\mathbb Q}$
. In order to apply Conjecture 2.3, we need to show that
![]() ${\mathfrak f}$
is nontrivial and new. As
${\mathfrak f}$
is nontrivial and new. As
![]() $\overline {\rho }_{E,p}$
is irreducible, the eigenform
$\overline {\rho }_{E,p}$
is irreducible, the eigenform
![]() ${\mathfrak f}$
is nontrivial. If
${\mathfrak f}$
is nontrivial. If
![]() ${\mathfrak f}$
is new, we are done. If not, we can replace it with an equivalent new eigenform of smaller level. Therefore, we can take
${\mathfrak f}$
is new, we are done. If not, we can replace it with an equivalent new eigenform of smaller level. Therefore, we can take
![]() ${\mathfrak f}$
new with level
${\mathfrak f}$
new with level
![]() ${\mathfrak N}'$
dividing
${\mathfrak N}'$
dividing
![]() ${\mathfrak N}_E$
. Finally, we apply Conjecture 2.3 and obtain that
${\mathfrak N}_E$
. Finally, we apply Conjecture 2.3 and obtain that
![]() ${\mathfrak f}$
either has an associated elliptic curve
${\mathfrak f}$
either has an associated elliptic curve
![]() $E_{{\mathfrak f}}/K$
of conductor
$E_{{\mathfrak f}}/K$
of conductor
![]() ${\mathfrak N}'$
, or has an associated fake elliptic curve
${\mathfrak N}'$
, or has an associated fake elliptic curve
![]() $A_{{\mathfrak f}}/K$
of conductor
$A_{{\mathfrak f}}/K$
of conductor
![]() ${\mathfrak N}_E^2$
.
${\mathfrak N}_E^2$
.
By Lemma 3.5, if
![]() $p>24$
, then
$p>24$
, then
![]() ${\mathfrak f}$
has an associated elliptic curve
${\mathfrak f}$
has an associated elliptic curve
![]() $E_{{\mathfrak f}}$
. As a result, we can assume that
$E_{{\mathfrak f}}$
. As a result, we can assume that
![]() $\overline {\rho }_{E,p}\sim \overline {\rho }_{E',p}$
where
$\overline {\rho }_{E,p}\sim \overline {\rho }_{E',p}$
where
![]() $E'=E_{{\mathfrak f}}$
is an elliptic curve with conductor
$E'=E_{{\mathfrak f}}$
is an elliptic curve with conductor
![]() ${\mathfrak N}'$
dividing
${\mathfrak N}'$
dividing
![]() ${\mathfrak N}_E$
.
${\mathfrak N}_E$
.
Lemma 3.5 [Reference Şengün and Siksek27, Lemma 7.3]
If
![]() $p>24$
, then
$p>24$
, then
![]() ${\mathfrak f}$
has an associated elliptic curve
${\mathfrak f}$
has an associated elliptic curve
![]() $E_{{\mathfrak f}}$
.
$E_{{\mathfrak f}}$
.
We can now give the proof of Theorem 3.1.
Proof of Theorem 3.1.
Lemma 3.5 gives us that if
![]() $p>24$
, then
$p>24$
, then
![]() ${\mathfrak f}$
has an associated elliptic curve
${\mathfrak f}$
has an associated elliptic curve
![]() $E_{{\mathfrak f}}$
. Therefore, by Lemma 3.4 we can assume that
$E_{{\mathfrak f}}$
. Therefore, by Lemma 3.4 we can assume that
![]() $\overline {\rho }_{E,p}\sim \overline {\rho }_{E',p}$
, where
$\overline {\rho }_{E,p}\sim \overline {\rho }_{E',p}$
, where
![]() $E'=E_{{\mathfrak f}}$
is an elliptic curve of conductor
$E'=E_{{\mathfrak f}}$
is an elliptic curve of conductor
![]() ${\mathfrak N}'$
dividing
${\mathfrak N}'$
dividing
![]() ${\mathfrak N}_E$
.
${\mathfrak N}_E$
.
Lemma 3.6 If
![]() $E'$
does not have a nontrivial K-rational point of order
$E'$
does not have a nontrivial K-rational point of order
![]() $3$
and is not isogenous to an elliptic curve with a nontrivial K-rational point of order
$3$
and is not isogenous to an elliptic curve with a nontrivial K-rational point of order
![]() $3$
, then
$3$
, then
![]() $p<C_{E'}$
where
$p<C_{E'}$
where
![]() $C_{E'}$
is a constant depending only on
$C_{E'}$
is a constant depending only on
![]() $E'$
.
$E'$
.
Proof By Theorem 3.7, there are infinitely many primes
![]() ${\mathfrak q}$
such that
${\mathfrak q}$
such that
![]() $\# E'({\mathbb F}_{\mathfrak q})\not \equiv 0\ \pmod 3$
. Fix such a prime
$\# E'({\mathbb F}_{\mathfrak q})\not \equiv 0\ \pmod 3$
. Fix such a prime
![]() ${\mathfrak q}\neq \lambda $
, and note that E is semistable at
${\mathfrak q}\neq \lambda $
, and note that E is semistable at
![]() ${\mathfrak q}$
. If E has good reduction at
${\mathfrak q}$
. If E has good reduction at
![]() ${\mathfrak q}$
, then
${\mathfrak q}$
, then
![]() $\# E({\mathbb F}_{\mathfrak q})\equiv \# E'({\mathbb F}_{\mathfrak q})\ \pmod p$
. Since
$\# E({\mathbb F}_{\mathfrak q})\equiv \# E'({\mathbb F}_{\mathfrak q})\ \pmod p$
. Since
![]() $3|\# E({\mathbb F}_{\mathfrak q})$
, the difference, which is divisible by p, is nonzero. As the difference belongs to a finite set depending on
$3|\# E({\mathbb F}_{\mathfrak q})$
, the difference, which is divisible by p, is nonzero. As the difference belongs to a finite set depending on
![]() ${\mathfrak q}$
, p becomes bounded. If E has multiplicative reduction at
${\mathfrak q}$
, p becomes bounded. If E has multiplicative reduction at
![]() ${\mathfrak q}$
, we obtain
${\mathfrak q}$
, we obtain
by comparing the traces of Frobenius. We see that this difference being also nonzero and depending only on
![]() ${\mathfrak q}$
gives a bound for p.
${\mathfrak q}$
gives a bound for p.
Now, suppose that
![]() $E'$
is
$E'$
is
![]() $3$
-isogenous to an elliptic curve
$3$
-isogenous to an elliptic curve
![]() $E"$
. As the isogeny induces an isomorphism
$E"$
. As the isogeny induces an isomorphism
![]() $E'[p]\cong E"[p]$
of Galois modules (
$E'[p]\cong E"[p]$
of Galois modules (
![]() $p\neq 3$
), we get
$p\neq 3$
), we get
![]() $\overline {\rho }_{E,p}\sim \overline {\rho }_{E',p}\sim \overline {\rho }_{E",p}$
completing the proof of (iii). After possibly replacing
$\overline {\rho }_{E,p}\sim \overline {\rho }_{E',p}\sim \overline {\rho }_{E",p}$
completing the proof of (iii). After possibly replacing
![]() $E'$
by
$E'$
by
![]() $E"$
, we can suppose that
$E"$
, we can suppose that
![]() $E'$
has a K-rational point of order
$E'$
has a K-rational point of order
![]() $3$
giving us (ii).
$3$
giving us (ii).
It remains to prove
![]() $v_{\lambda }(j')<0$
where
$v_{\lambda }(j')<0$
where
![]() $j'$
is the j-invariant of
$j'$
is the j-invariant of
![]() $E'$
. By Lemma 5.2 of [Reference Şengün and Siksek27], p divides the size of
$E'$
. By Lemma 5.2 of [Reference Şengün and Siksek27], p divides the size of
![]() $\overline {\rho }_{E,p}(I_{\lambda })$
. Now, Lemma 2.5 implies that
$\overline {\rho }_{E,p}(I_{\lambda })$
. Now, Lemma 2.5 implies that
![]() $v_{\lambda }(j')<0$
since the sizes of
$v_{\lambda }(j')<0$
since the sizes of
![]() $\overline {\rho }_{E,p}(I_{\lambda })$
and
$\overline {\rho }_{E,p}(I_{\lambda })$
and
![]() $\overline {\rho }_{E',p}(I_{\lambda })$
are equal.
$\overline {\rho }_{E',p}(I_{\lambda })$
are equal.
The following theorem of Katz is used in the proof of the above lemma.
Theorem 3.7 [Reference Katz18, Theorem 2]
Let E be an elliptic curve over a number field K, and let
![]() $m\geq 2$
be, an integer. For each prime
$m\geq 2$
be, an integer. For each prime
![]() $\mathfrak {p}$
of K at which E has good reduction let
$\mathfrak {p}$
of K at which E has good reduction let
![]() $N(\mathfrak {p})$
denote the number of
$N(\mathfrak {p})$
denote the number of
![]() $\mathbb {F}_{\mathfrak {p}}$
-rational points on
$\mathbb {F}_{\mathfrak {p}}$
-rational points on
![]() $E\mod {\mathfrak {p}}$
. If we have
$E\mod {\mathfrak {p}}$
. If we have
for a set of primes
![]() $\mathfrak {p}$
of density one in K, then there exists a K-isogenous elliptic curve
$\mathfrak {p}$
of density one in K, then there exists a K-isogenous elliptic curve
![]() $E'$
defined over K such that
$E'$
defined over K such that
3.2 Irreducibility of Galois representations
Throughout this subsection,
![]() $K={\mathbb Q}(\sqrt {-d})$
, where
$K={\mathbb Q}(\sqrt {-d})$
, where
![]() $d \in \{1,7,19,43,67\}$
,
$d \in \{1,7,19,43,67\}$
,
![]() $(a,b,c) \in \mathcal O_K$
, is a nontrivial, primitive, putative solution of the equation
$(a,b,c) \in \mathcal O_K$
, is a nontrivial, primitive, putative solution of the equation
![]() $x^p+y^p=z^3$
.
$x^p+y^p=z^3$
.
The idea of this section is to prove that when p is bigger than an explicit constant, then the mod p Galois representation
![]() $\overline {\rho }_{E,p}:G_{\mathbb Q} \rightarrow \operatorname {\mathrm {Aut}}(E[p]) \cong \operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
attached to E is absolutely irreducible.
$\overline {\rho }_{E,p}:G_{\mathbb Q} \rightarrow \operatorname {\mathrm {Aut}}(E[p]) \cong \operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
attached to E is absolutely irreducible.
We will use the following result of Freitas and Siksek.
Lemma 3.8 [Reference Freitas and Siksek13, Lemma 6.3]
Let E be an elliptic curve over a number field K with conductor
![]() $\mathcal {N}_E$
, and let p be a prime
$\mathcal {N}_E$
, and let p be a prime
![]() $>5$
. Suppose that
$>5$
. Suppose that
![]() $\rho _p=\overline {\rho }_{E,p}$
is reducible. Write
$\rho _p=\overline {\rho }_{E,p}$
is reducible. Write
 $\rho _p \sim \begin {pmatrix} \theta & * \\ 0 & \theta ' \end {pmatrix} $
, where
$\rho _p \sim \begin {pmatrix} \theta & * \\ 0 & \theta ' \end {pmatrix} $
, where
![]() $\theta , \theta ': G_{K} \rightarrow \mathbb F_p^*$
are the isogeny characters. Let
$\theta , \theta ': G_{K} \rightarrow \mathbb F_p^*$
are the isogeny characters. Let
![]() $\mathcal N_{\theta }, \mathcal N_{\theta '}$
denote the conductors of these characters. Fix a prime
$\mathcal N_{\theta }, \mathcal N_{\theta '}$
denote the conductors of these characters. Fix a prime
![]() $\mathfrak q \nmid p$
of
$\mathfrak q \nmid p$
of
![]() $\mathcal O_K.$
$\mathcal O_K.$
We have the following:
-
• If E has good or multiplicative reduction at
 $\mathfrak q$
, then
$\mathfrak q$
, then
 $v_{\mathfrak q}(\mathcal N_{\theta })=v_{\mathfrak q}(\mathcal N_{\theta '})=0$
.
$v_{\mathfrak q}(\mathcal N_{\theta })=v_{\mathfrak q}(\mathcal N_{\theta '})=0$
. -
• If E has additive reduction at
 $\mathfrak q$
, then
$\mathfrak q$
, then
 $v_{\mathfrak q}(\mathcal N_E)$
is even and
$v_{\mathfrak q}(\mathcal N_E)$
is even and
 $v_{\mathfrak q}(\mathcal N_{\theta })=v_{\mathfrak q}(\mathcal N_{\theta '})=v_{\mathfrak q}(\mathcal N_E)/2.$
$v_{\mathfrak q}(\mathcal N_{\theta })=v_{\mathfrak q}(\mathcal N_{\theta '})=v_{\mathfrak q}(\mathcal N_E)/2.$
Proposition 3.9 Let
![]() $E/K$
be the Frey curve attached to a putative solution to equation (
1.1
), and let
$E/K$
be the Frey curve attached to a putative solution to equation (
1.1
), and let
![]() $p> C_K$
be a prime where
$p> C_K$
be a prime where
![]() $C_K$
is defined as below. Then
$C_K$
is defined as below. Then
![]() $\overline {\rho }_{E,p}$
is irreducible.
$\overline {\rho }_{E,p}$
is irreducible.
![]() $C_K=47$
if the equation
$C_K=47$
if the equation
![]() $y^3+24b^pcy+16b^{2p} \equiv 0\ \pmod {\lambda ^2}$
has a solution in the ring of integers of the local field
$y^3+24b^pcy+16b^{2p} \equiv 0\ \pmod {\lambda ^2}$
has a solution in the ring of integers of the local field
![]() $K_\lambda $
, and otherwise
$K_\lambda $
, and otherwise
![]() $C_K=44,483$
.
$C_K=44,483$
.
Proof Suppose that
![]() $\rho _p=\overline {\rho }_{E,p}$
is reducible. Write
$\rho _p=\overline {\rho }_{E,p}$
is reducible. Write
 $\rho _p \sim \begin {pmatrix} \theta & * \\ 0 & \theta ' \end {pmatrix} $
, where
$\rho _p \sim \begin {pmatrix} \theta & * \\ 0 & \theta ' \end {pmatrix} $
, where
![]() $\theta , \theta ': G_{K} \rightarrow \mathbb F_p^*$
are the isogeny characters. Let
$\theta , \theta ': G_{K} \rightarrow \mathbb F_p^*$
are the isogeny characters. Let
![]() $\mathcal N_{\theta }, \mathcal N_{\theta '}$
denote the conductors of these characters. Fix a prime
$\mathcal N_{\theta }, \mathcal N_{\theta '}$
denote the conductors of these characters. Fix a prime
![]() $\mathfrak q \nmid 3p$
of
$\mathfrak q \nmid 3p$
of
![]() $\mathcal O_K.$
By [Reference Freitas and Siksek13, Lemma 6.3], we get
$\mathcal O_K.$
By [Reference Freitas and Siksek13, Lemma 6.3], we get
![]() $v_{\mathfrak q}(\mathcal N_{\theta })=v_{\mathfrak q}(\mathcal N_{\theta '})=0$
since E is semistable away from
$v_{\mathfrak q}(\mathcal N_{\theta })=v_{\mathfrak q}(\mathcal N_{\theta '})=0$
since E is semistable away from
![]() $\lambda $
.
$\lambda $
.
By Lemmas 2.4 and 3.8,
![]() $v_{\lambda }(\mathcal N_{\theta })=v_{\lambda }(\mathcal N_{\theta '}) \in \{0,1\}$
.
$v_{\lambda }(\mathcal N_{\theta })=v_{\lambda }(\mathcal N_{\theta '}) \in \{0,1\}$
.
Now, we deal with
![]() ${\mathfrak p} | p.$
${\mathfrak p} | p.$
-
(1) Say
 $\mathcal N_{\theta }$
or
$\mathcal N_{\theta }$
or
 $\mathcal N_{\theta '}$
is relatively prime to p. Note that interchanging
$\mathcal N_{\theta '}$
is relatively prime to p. Note that interchanging
 $\theta $
and
$\theta $
and
 $\theta '$
corresponds to replacing E with an isogenous elliptic curve
$\theta '$
corresponds to replacing E with an isogenous elliptic curve
 $E/\ker \theta $
. Since
$E/\ker \theta $
. Since
 $\ker \theta $
is a K-rational subgroup of
$\ker \theta $
is a K-rational subgroup of
 $E[p]$
of order p, the elliptic curves E and
$E[p]$
of order p, the elliptic curves E and
 $E/\ker \theta $
are p-isogenous. Therefore, without loss of generality, assume that
$E/\ker \theta $
are p-isogenous. Therefore, without loss of generality, assume that
 $(p,\mathcal N_{\theta })=1$
and
$(p,\mathcal N_{\theta })=1$
and
 $v_{{\mathfrak p}}(\mathcal N_{\theta })=0$
for all
$v_{{\mathfrak p}}(\mathcal N_{\theta })=0$
for all
 ${\mathfrak p} | p$
as in the previous case. We also have
${\mathfrak p} | p$
as in the previous case. We also have
 $v_{\mathfrak q}(\mathcal N_{\theta })=0$
for all
$v_{\mathfrak q}(\mathcal N_{\theta })=0$
for all
 $\mathfrak q \nmid 3p$
, as explained above. Therefore,
$\mathfrak q \nmid 3p$
, as explained above. Therefore,
 $\mathcal N_{\theta }=\lambda ^m$
, where
$\mathcal N_{\theta }=\lambda ^m$
, where
 $m=0$
or
$m=0$
or
 $1$
, which implies that
$1$
, which implies that
 $\theta $
is a character of the ray class group of modulus
$\theta $
is a character of the ray class group of modulus
 $\lambda ^m$
of K.
$\lambda ^m$
of K.Using Magma, we computed the ray class groups for these moduli and get the following groups only:
 $$ \begin{align*}\{1\}, {\mathbb Z}/2{\mathbb Z}, {\mathbb Z}/4{\mathbb Z} .\end{align*} $$
$$ \begin{align*}\{1\}, {\mathbb Z}/2{\mathbb Z}, {\mathbb Z}/4{\mathbb Z} .\end{align*} $$
-
• If the order of
 $\theta $
is one then
$\theta $
is one then
 $\theta $
is trivial. Then
$\theta $
is trivial. Then
 $\rho _p \sim \begin {pmatrix} 1 & * \\ 0 & \theta ' \end {pmatrix} $
, and this implies that E has a K-rational point of order p. By Lemma 2.4, E has also a point of order
$\rho _p \sim \begin {pmatrix} 1 & * \\ 0 & \theta ' \end {pmatrix} $
, and this implies that E has a K-rational point of order p. By Lemma 2.4, E has also a point of order
 $3$
, then
$3$
, then
 $E(K)$
has a
$E(K)$
has a
 $3p$
-torsion point, but by the work of Kamienney, Kenku, and Momose [Reference Kamienny16, Reference Kenku and Momose19], this is not possible when
$3p$
-torsion point, but by the work of Kamienney, Kenku, and Momose [Reference Kamienny16, Reference Kenku and Momose19], this is not possible when
 $p \geq 7$
, hence a contradiction.
$p \geq 7$
, hence a contradiction. -
• If the order of
 $\theta $
is two, then we can conclude that E has a point of order
$\theta $
is two, then we can conclude that E has a point of order
 $3p$
over a quadratic extension L of K and get a contradiction since, by [Reference Derickx and Kamienny8],
$3p$
over a quadratic extension L of K and get a contradiction since, by [Reference Derickx and Kamienny8],
 $E(L)[p]=\{0\}$
if
$E(L)[p]=\{0\}$
if
 $p>17$
. Here, L is the number field cut out by the character
$p>17$
. Here, L is the number field cut out by the character
 $\theta ^2$
, i.e.,
$\theta ^2$
, i.e.,
 $|L:{\mathbb Q}|=4.$
$|L:{\mathbb Q}|=4.$
-
• If the order of
 $\theta $
is four, let L be the unique quadratic extension of K cut out by
$\theta $
is four, let L be the unique quadratic extension of K cut out by
 $\theta ^2$
. Then
$\theta ^2$
. Then
 $\theta _{G_L}$
is quadratic. Let
$\theta _{G_L}$
is quadratic. Let
 $E'$
be the twist of E by
$E'$
be the twist of E by
 $\theta _{G_L}$
. The elliptic curve
$\theta _{G_L}$
. The elliptic curve
 $E'$
is also over L and has a point of order p as in the previous case. Again, we get a contradiction by [Reference Derickx and Kamienny8].
$E'$
is also over L and has a point of order p as in the previous case. Again, we get a contradiction by [Reference Derickx and Kamienny8].
-
-
(2) Now, we are left with the case that neither
 $\mathcal N_{\theta }$
nor
$\mathcal N_{\theta }$
nor
 $\mathcal N_{\theta '}$
is relatively prime to p. Recall that E is semistable away from
$\mathcal N_{\theta '}$
is relatively prime to p. Recall that E is semistable away from
 $\lambda $
and p is not ramified in K. Then either p is inert or p splits in K.
$\lambda $
and p is not ramified in K. Then either p is inert or p splits in K.-
(a) p is inert in K: By [Reference Freitas and Siksek13, Corollary 6.2], E cannot have good supersingular reduction at p. Therefore, E has good ordinary or multiplicative reduction at p and
(3.1)(see [Reference Coates and Yau4, Section 3]), where $$ \begin{align} \rho_p|_{I_p} \sim \begin{pmatrix} \chi_p & * \\ 0 & 1 \end{pmatrix} \end{align} $$
$$ \begin{align} \rho_p|_{I_p} \sim \begin{pmatrix} \chi_p & * \\ 0 & 1 \end{pmatrix} \end{align} $$
 $\chi _p$
is the mod p cyclotomic character. By [Reference Kraus21, Lemma 1], p has to be relatively prime with
$\chi _p$
is the mod p cyclotomic character. By [Reference Kraus21, Lemma 1], p has to be relatively prime with
 $\mathcal N_{\theta }$
or
$\mathcal N_{\theta }$
or
 $\mathcal N_{\theta '}$
, which contradicts to the assumption of item (2).
$\mathcal N_{\theta '}$
, which contradicts to the assumption of item (2).
-
(b) p splits in K: Say
 $p=\mathcal P \mathcal P'$
and
$p=\mathcal P \mathcal P'$
and
 $\mathcal P | \mathcal N_{\theta }, \mathcal P' \nmid \mathcal N_{\theta }$
and
$\mathcal P | \mathcal N_{\theta }, \mathcal P' \nmid \mathcal N_{\theta }$
and
 $\mathcal P \nmid \mathcal N_{\theta '}, \mathcal P' | \mathcal N_{\theta '}$
. By [Reference Freitas and Siksek13, Corollary 6.2], we know that E has good ordinary or multiplicative reduction at
$\mathcal P \nmid \mathcal N_{\theta '}, \mathcal P' | \mathcal N_{\theta '}$
. By [Reference Freitas and Siksek13, Corollary 6.2], we know that E has good ordinary or multiplicative reduction at
 $\mathcal P$
and
$\mathcal P$
and
 $ \mathcal P'$
by equation (3.1), we see that one of the characters
$ \mathcal P'$
by equation (3.1), we see that one of the characters
 $\theta , \theta '$
is ramified at
$\theta , \theta '$
is ramified at
 $\mathcal P$
and the other is ramified at
$\mathcal P$
and the other is ramified at
 $\mathcal P'$
,
$\mathcal P'$
,
 $\theta |_{I_{\mathcal P}} = \chi _p|_{\mathcal P}$
, and
$\theta |_{I_{\mathcal P}} = \chi _p|_{\mathcal P}$
, and
 $\theta '|_{ I_{\mathcal P'}} = \chi _p|_{\mathcal P'}$
. Hence,
$\theta '|_{ I_{\mathcal P'}} = \chi _p|_{\mathcal P'}$
. Hence,
 $\theta $
is unramified away from
$\theta $
is unramified away from
 $\mathcal P$
and
$\mathcal P$
and
 $ \lambda $
since all bad places of E except possibly
$ \lambda $
since all bad places of E except possibly
 $\lambda $
are of potentially multiplicative reduction.
$\lambda $
are of potentially multiplicative reduction.-
(i)
 $\lambda $
divides
$\lambda $
divides
 $ab$
: In this case, by Lemma 2.4, E has multiplicative or good reduction at
$ab$
: In this case, by Lemma 2.4, E has multiplicative or good reduction at
 $\lambda $
; therefore, we can say that
$\lambda $
; therefore, we can say that
 $\theta $
is unramified away from
$\theta $
is unramified away from
 $\mathcal P$
. The character
$\mathcal P$
. The character
 $\theta ^2|_{I_{\mathcal P}}=\chi _p^2|_{I_{\mathcal P}}$
is also unramified away from
$\theta ^2|_{I_{\mathcal P}}=\chi _p^2|_{I_{\mathcal P}}$
is also unramified away from
 $\mathcal P$
; therefore, by [Reference Ţurcaş31, Lemma 4.3],
$\mathcal P$
; therefore, by [Reference Ţurcaş31, Lemma 4.3],
 $\theta (\sigma _\lambda ) \equiv \text {Norm}_{K_{\mathcal P}/{\mathbb Q}_p}(\alpha )^2\ \pmod p$
, where
$\theta (\sigma _\lambda ) \equiv \text {Norm}_{K_{\mathcal P}/{\mathbb Q}_p}(\alpha )^2\ \pmod p$
, where
 $\sigma _\lambda $
is the Frobenius automorphism at
$\sigma _\lambda $
is the Frobenius automorphism at
 $\lambda = \langle 3 \rangle $
. We also know that, by [Reference Şengün and Siksek27, Lemma 6.3],
$\lambda = \langle 3 \rangle $
. We also know that, by [Reference Şengün and Siksek27, Lemma 6.3],
 $\theta ^2(\sigma _\lambda ) \equiv 1\ \pmod p$
(note that E has multiplicative reduction at
$\theta ^2(\sigma _\lambda ) \equiv 1\ \pmod p$
(note that E has multiplicative reduction at
 $\lambda $
). Therefore, we have
$\lambda $
). Therefore, we have
 $p | \text {Norm}_{K_{\mathcal P}/{\mathbb Q}_p}(\lambda )^2 - 1$
, a contradiction since
$p | \text {Norm}_{K_{\mathcal P}/{\mathbb Q}_p}(\lambda )^2 - 1$
, a contradiction since
 $p>20$
.
$p>20$
. -
(ii)
 $\lambda $
does not divide
$\lambda $
does not divide
 $ab$
: In this case, by Lemma 2.4, E has additive reduction at
$ab$
: In this case, by Lemma 2.4, E has additive reduction at
 $\lambda $
, so the above argument fails. Recall that
$\lambda $
, so the above argument fails. Recall that
 $v_\lambda (\Delta _E)=v_{\lambda }(3^3b^{3p}a^p)=3$
and
$v_\lambda (\Delta _E)=v_{\lambda }(3^3b^{3p}a^p)=3$
and
 $v_\lambda (c_6(E))=3$
. By [Reference Kraus20, p. 356], we see that
$v_\lambda (c_6(E))=3$
. By [Reference Kraus20, p. 356], we see that
 $\theta ^4$
or
$\theta ^4$
or
 $\theta ^{12}$
is unramified at
$\theta ^{12}$
is unramified at
 $\lambda $
. The case
$\lambda $
. The case
 $\theta ^{12}$
happens when the equation
$\theta ^{12}$
happens when the equation
 $y^3+24b^pcy+16b^{2p} \equiv 0 \ \pmod \lambda ^2$
does not have a solution. Therefore, we have
$y^3+24b^pcy+16b^{2p} \equiv 0 \ \pmod \lambda ^2$
does not have a solution. Therefore, we have
 $\theta ^4|_{I_{\mathcal P}}=\chi _p^4|_{I_{\mathcal P}}$
is unramified away from
$\theta ^4|_{I_{\mathcal P}}=\chi _p^4|_{I_{\mathcal P}}$
is unramified away from
 $\mathcal P$
or
$\mathcal P$
or
 $\theta ^{12}|_{I_{\mathcal P}}=\chi _p^{12}|_{I_{\mathcal P}}$
is unramified away from
$\theta ^{12}|_{I_{\mathcal P}}=\chi _p^{12}|_{I_{\mathcal P}}$
is unramified away from
 $\mathcal P$
.
$\mathcal P$
.By [Reference Ţurcaş31, Lemma 4.3],
 $\theta ^4(\sigma _{\mathfrak P}) \equiv \text {Norm}_{K_{\mathcal P}/{\mathbb Q}_p}(\alpha )^2=9 \ \pmod p$
, where
$\theta ^4(\sigma _{\mathfrak P}) \equiv \text {Norm}_{K_{\mathcal P}/{\mathbb Q}_p}(\alpha )^2=9 \ \pmod p$
, where
 $\alpha $
is a nonzero prime-to-p element of K and
$\alpha $
is a nonzero prime-to-p element of K and
 $\sigma _{\mathfrak P}$
is the Frobenius automorphism at
$\sigma _{\mathfrak P}$
is the Frobenius automorphism at
 $\mathfrak P=\langle \alpha \rangle $
. Therefore, the polynomial
$\mathfrak P=\langle \alpha \rangle $
. Therefore, the polynomial
 $x^4-9$
has a root
$x^4-9$
has a root
 $\theta (\sigma _{\mathfrak P})$
modulo p. Recall that E has potentially good reduction at
$\theta (\sigma _{\mathfrak P})$
modulo p. Recall that E has potentially good reduction at
 $\lambda $
since
$\lambda $
since
 $v_\lambda (j_E)>0$
. Let
$v_\lambda (j_E)>0$
. Let
 $P_\lambda (x)$
be the characteristic polynomial of the Frobenius of E at
$P_\lambda (x)$
be the characteristic polynomial of the Frobenius of E at
 $\lambda $
. Since
$\lambda $
. Since
 $\rho _p \sim \begin {pmatrix} \theta & * \\ 0 & \theta ' \end {pmatrix} $
, we get
$\rho _p \sim \begin {pmatrix} \theta & * \\ 0 & \theta ' \end {pmatrix} $
, we get
 $P_\lambda (x) \equiv (x-\theta (\sigma _\lambda ))(x-\theta '(\sigma _\lambda )) \ \pmod p$
.
$P_\lambda (x) \equiv (x-\theta (\sigma _\lambda ))(x-\theta '(\sigma _\lambda )) \ \pmod p$
.Hence, we can conclude that
 $p | \operatorname {\mathrm {Res}}(x^4-9, P_\lambda (x))$
, where
$p | \operatorname {\mathrm {Res}}(x^4-9, P_\lambda (x))$
, where
 $\operatorname {\mathrm {Res}}$
denotes the resultant of the polynomials. Note that
$\operatorname {\mathrm {Res}}$
denotes the resultant of the polynomials. Note that
 $P_\lambda (x) \in \mathbb Z[x]$
and its roots have absolute value less than or equal to
$P_\lambda (x) \in \mathbb Z[x]$
and its roots have absolute value less than or equal to
 $\sqrt {\operatorname {\mbox { Norm}}(\lambda )}=3$
(see [Reference David6, Proposition 1.6]). Then the possibilities for
$\sqrt {\operatorname {\mbox { Norm}}(\lambda )}=3$
(see [Reference David6, Proposition 1.6]). Then the possibilities for
 $P_\lambda (x)$
are as follows:
$P_\lambda (x)$
are as follows:  $$ \begin{align*}P_1(x)&=x^2+9, P_2(x)=x^2-x+9, P_3(x)=x^2-2x+9,\\[4pt]P_4(x)&=x^2+x+9, P_5(x)=x^2+2x+9,\\[4pt]P_6(x)&=x^2+3x+9, P_7(x)=x^2-3x+9 , P_8(x)=x^2+4x+9,\\[4pt]P_9(x)&=x^2-4x+9,\\[4pt]P_{10}(x)&=x^2+5x+9, P_{11}(x)=x^2-5x+9, P_{12}(x)=x^2+6x+9,\\[4pt]P_{13}(x)&=x^2-6x+9.\end{align*} $$
$$ \begin{align*}P_1(x)&=x^2+9, P_2(x)=x^2-x+9, P_3(x)=x^2-2x+9,\\[4pt]P_4(x)&=x^2+x+9, P_5(x)=x^2+2x+9,\\[4pt]P_6(x)&=x^2+3x+9, P_7(x)=x^2-3x+9 , P_8(x)=x^2+4x+9,\\[4pt]P_9(x)&=x^2-4x+9,\\[4pt]P_{10}(x)&=x^2+5x+9, P_{11}(x)=x^2-5x+9, P_{12}(x)=x^2+6x+9,\\[4pt]P_{13}(x)&=x^2-6x+9.\end{align*} $$
We computed these 13 resultants, and none of them has a prime divisor greater than
 $ 47 $
. Since
$ 47 $
. Since
 $p>47$
, we get a contradiction.
$p>47$
, we get a contradiction.For the case of
 $\theta ^{12}|_{I_{\mathcal P}}=\chi _p^{12}|_{I_{\mathcal P}}$
, similarly we need to compute the resultants of
$\theta ^{12}|_{I_{\mathcal P}}=\chi _p^{12}|_{I_{\mathcal P}}$
, similarly we need to compute the resultants of
 $P_i$
with
$P_i$
with
 $x^{12}-9$
and see that none of them has a prime divisor greater than
$x^{12}-9$
and see that none of them has a prime divisor greater than
 $44,483$
.
$44,483$
.
-
-
In this corollary, we will summarize the cases where we have absolute irreducibility.
Corollary 3.10
-
(1) Let p be odd. If
 $\lambda | ab$
and
$\lambda | ab$
and
 $\overline {\rho }_{E,p}$
is irreducible, then
$\overline {\rho }_{E,p}$
is irreducible, then
 $\overline {\rho }_{E,p}$
is absolutely irreducible.
$\overline {\rho }_{E,p}$
is absolutely irreducible. -
(2) Assume that
 $\lambda \nmid ab$
. Let K be an imaginary quadratic field, and let
$\lambda \nmid ab$
. Let K be an imaginary quadratic field, and let
 $p> M_K$
for some effectively computable constant
$p> M_K$
for some effectively computable constant
 $M_K$
depending only on K.
$M_K$
depending only on K.-
(a) Say p splits in K and
 $p \equiv 3 \ \pmod 4$
. If
$p \equiv 3 \ \pmod 4$
. If
 $\overline {\rho }_{E,p}$
is irreducible, then
$\overline {\rho }_{E,p}$
is irreducible, then
 $\overline {\rho }_{E,p}$
is absolutely irreducible.
$\overline {\rho }_{E,p}$
is absolutely irreducible. -
(b) Say
 $p \equiv 1\ \pmod 3$
and
$p \equiv 1\ \pmod 3$
and
 $\overline {\rho }_{E,p}(I_\lambda )$
is divisible by
$\overline {\rho }_{E,p}(I_\lambda )$
is divisible by
 $3$
(which means that the inertia has order
$3$
(which means that the inertia has order
 $12$
and this happens if and only if
$12$
and this happens if and only if
 $y^3+24b^pcy+16b^{2p} \equiv 0 \ \pmod {\lambda ^2}$
does not have a solution). If
$y^3+24b^pcy+16b^{2p} \equiv 0 \ \pmod {\lambda ^2}$
does not have a solution). If
 $\overline {\rho }_{E,p}$
is irreducible, then
$\overline {\rho }_{E,p}$
is irreducible, then
 $\overline {\rho }_{E,p}$
is absolutely irreducible.
$\overline {\rho }_{E,p}$
is absolutely irreducible.
-
-
(3) Let p be odd. If K is totally real, then
 $\overline {\rho }_{E,p}$
is irreducible if and only if it is absolutely irreducible.
$\overline {\rho }_{E,p}$
is irreducible if and only if it is absolutely irreducible.
Proof
-
(1) The Frey curve E attached to a putative primitive solution
 $(a,b,c)\in \mathcal O_K^3$
of
$(a,b,c)\in \mathcal O_K^3$
of
 $x^p+y^p=z^3$
is semistable when
$x^p+y^p=z^3$
is semistable when
 $\lambda | ab$
where
$\lambda | ab$
where
 $\lambda $
is the prime of
$\lambda $
is the prime of
 $\mathcal O_K$
lying over
$\mathcal O_K$
lying over
 $3$
. These were discussed in Lemma 2.4. By Proposition 3.9, we know that
$3$
. These were discussed in Lemma 2.4. By Proposition 3.9, we know that
 $\overline {\rho }_{E,p}$
is irreducible when p is big enough. In Proposition 3.9, we make this bound explicit. Recall that the j-invariant of E is
$\overline {\rho }_{E,p}$
is irreducible when p is big enough. In Proposition 3.9, we make this bound explicit. Recall that the j-invariant of E is
 $j_E=\frac {3^3c^3(9a^p+b^p)^3}{(ab^3)^p}$
. Therefore,
$j_E=\frac {3^3c^3(9a^p+b^p)^3}{(ab^3)^p}$
. Therefore,
 $v_{\lambda }(j_E)=3v_{\lambda }(3)-3pv_{\lambda }(b)<0$
and
$v_{\lambda }(j_E)=3v_{\lambda }(3)-3pv_{\lambda }(b)<0$
and
 $p\nmid v_{\lambda }(j_E)$
when
$p\nmid v_{\lambda }(j_E)$
when
 $p>5$
. Therefore, by the theory of Tate curve, the inertia group
$p>5$
. Therefore, by the theory of Tate curve, the inertia group
 $I_{\lambda }$
contains an element which acts on
$I_{\lambda }$
contains an element which acts on
 $E[p]$
via
$E[p]$
via
 $\begin {pmatrix} 1& 1\\ 0 & 1 \end {pmatrix}$
which has order p. By Theorem 2.7, the image
$\begin {pmatrix} 1& 1\\ 0 & 1 \end {pmatrix}$
which has order p. By Theorem 2.7, the image
 $\overline {\rho }_{E,p}$
contains
$\overline {\rho }_{E,p}$
contains
 $\operatorname {\mathrm {SL}}_2(\mathbb F_p)$
and hence is an absolutely irreducible group of
$\operatorname {\mathrm {SL}}_2(\mathbb F_p)$
and hence is an absolutely irreducible group of
 $\operatorname {\mathrm {GL}}_2(\mathbb F_p)$
.
$\operatorname {\mathrm {GL}}_2(\mathbb F_p)$
. -
(2) Assume that
 $\lambda \nmid ab$
. We will use the below theorem of Larson and Vaintrob (Theorem 3.11).
$\lambda \nmid ab$
. We will use the below theorem of Larson and Vaintrob (Theorem 3.11).Assume that
 $\overline {\rho }_{E,p}$
is irreducible but absolutely reducible. Then, by Part 1 of Theorem 2.7, p cannot divide the order of
$\overline {\rho }_{E,p}$
is irreducible but absolutely reducible. Then, by Part 1 of Theorem 2.7, p cannot divide the order of
 $\overline {\rho }_{E,p}(G_K)$
. By the second part of the same theorem, for big enough p, the image
$\overline {\rho }_{E,p}(G_K)$
. By the second part of the same theorem, for big enough p, the image
 $\overline {\rho }_{E,p}(G_K)$
is in a nonsplit Cartan subgroup or it is in the normalizer of a Cartan subgroup but not in the Cartan itself. Now, we will rule out the second case. Say
$\overline {\rho }_{E,p}(G_K)$
is in a nonsplit Cartan subgroup or it is in the normalizer of a Cartan subgroup but not in the Cartan itself. Now, we will rule out the second case. Say
 $\overline {\rho }_{E,p}(G_K)$
has an element g which is not in nonsplit Cartan but in the normalizer of nonsplit Cartan. Let h be any element of the nonsplit Cartan subgroup different from the identity element. Then h and g do not share a common eigenvector, and this contradicts to the assumption that
$\overline {\rho }_{E,p}(G_K)$
has an element g which is not in nonsplit Cartan but in the normalizer of nonsplit Cartan. Let h be any element of the nonsplit Cartan subgroup different from the identity element. Then h and g do not share a common eigenvector, and this contradicts to the assumption that
 $\overline {\rho }_{E,p}(G_K)$
is absolutely reducible.
$\overline {\rho }_{E,p}(G_K)$
is absolutely reducible.Similar argument can be made if
 $\overline {\rho }_{E,p}(G_K)$
is in the normalizer of a split Cartan case but not in the split Cartan itself.
$\overline {\rho }_{E,p}(G_K)$
is in the normalizer of a split Cartan case but not in the split Cartan itself.Therefore, we can conclude that
 $\overline {\rho }_{E,p}(G_K)$
is in a nonsplit Cartan subgroup. The rest of the argument is similar as in [Reference Najman and Ţurcaş24]. Up to conjugation,
$\overline {\rho }_{E,p}(G_K)$
is in a nonsplit Cartan subgroup. The rest of the argument is similar as in [Reference Najman and Ţurcaş24]. Up to conjugation,
 $\overline {\rho }_{E,p} \otimes \mathbb {F}_p \sim \begin {pmatrix} \lambda & 0\\ 0 & \lambda ^p \end {pmatrix}$
, where
$\overline {\rho }_{E,p} \otimes \mathbb {F}_p \sim \begin {pmatrix} \lambda & 0\\ 0 & \lambda ^p \end {pmatrix}$
, where
 $\lambda : G_K \rightarrow {\mathbb F}_{p^2}$
and
$\lambda : G_K \rightarrow {\mathbb F}_{p^2}$
and
 $\lambda ^{p+1}=\chi _p$
, where
$\lambda ^{p+1}=\chi _p$
, where
 $\chi _p$
is the cyclotomic character.
$\chi _p$
is the cyclotomic character.-
(a) Assume that p splits in K and
 $p \equiv 3 \ \pmod 4$
. We will assume that
$p \equiv 3 \ \pmod 4$
. We will assume that
 $\overline {\rho }_{E,p}$
is irreducible but absolutely reducible and get a contradiction. We will apply the above theorem to the elliptic curve E attached to a putative solution of equation (1.1). Assuming that the prime p is greater than the constant given in the theorem, we get a complex multiplication (CM) elliptic curve
$\overline {\rho }_{E,p}$
is irreducible but absolutely reducible and get a contradiction. We will apply the above theorem to the elliptic curve E attached to a putative solution of equation (1.1). Assuming that the prime p is greater than the constant given in the theorem, we get a complex multiplication (CM) elliptic curve
 $E'/K$
with
$E'/K$
with
 $\overline {\rho }_{E',p} \otimes \overline {\mathbb F}_p \sim \begin {pmatrix} \theta & 0\\ 0 & \theta ' \end {pmatrix}$
such that
$\overline {\rho }_{E',p} \otimes \overline {\mathbb F}_p \sim \begin {pmatrix} \theta & 0\\ 0 & \theta ' \end {pmatrix}$
such that
 $\theta ^{12} = \lambda ^{12}.$
$\theta ^{12} = \lambda ^{12}.$
Since p splits in K, we see that the image
 $\overline {\rho }_{E',p}(G_K)$
is contained inside a split Cartan subgroup, which implies that the character
$\overline {\rho }_{E',p}(G_K)$
is contained inside a split Cartan subgroup, which implies that the character
 $\theta $
is in fact
$\theta $
is in fact
 $\mathbb {F}_p$
-valued. In particular, the order of
$\mathbb {F}_p$
-valued. In particular, the order of
 $\theta $
is divisible by
$\theta $
is divisible by
 $p-1.$
$p-1.$
We also know that, by Theorem 1 of [Reference Larson and Vaintrob22],
 $\lambda \theta ^{-1}$
is unramified away from the additive primes of E. Therefore,
$\lambda \theta ^{-1}$
is unramified away from the additive primes of E. Therefore,
 $\lambda \theta ^{-1}$
is unramified at
$\lambda \theta ^{-1}$
is unramified at
 $\mathcal P | p.$
Since
$\mathcal P | p.$
Since
 $\lambda ^{p+1}=\chi _p$
, we get
$\lambda ^{p+1}=\chi _p$
, we get
 $\theta ^{p+1}|_{I_{\mathcal P}}=\chi _p|_{I_{\mathcal P}}$
. Note that
$\theta ^{p+1}|_{I_{\mathcal P}}=\chi _p|_{I_{\mathcal P}}$
. Note that
 $p \equiv 3 \ \pmod 4$
,
$p \equiv 3 \ \pmod 4$
,
 $\frac {p-1}{2}$
is odd. We deduce that
$\frac {p-1}{2}$
is odd. We deduce that
 $\chi _p^{(p-1)/2}|_{I_{\mathcal P}} = (\theta ^{p-1})^{(p+1)/2}|_{I_{\mathcal P}} = 1$
. However, the order of
$\chi _p^{(p-1)/2}|_{I_{\mathcal P}} = (\theta ^{p-1})^{(p+1)/2}|_{I_{\mathcal P}} = 1$
. However, the order of
 $\chi _p^{(p-1)/2}|_{I_{\mathcal P}} $
is
$\chi _p^{(p-1)/2}|_{I_{\mathcal P}} $
is
 $p-1$
since it surjects on
$p-1$
since it surjects on
 $\mathbb F_p^{*}$
.
$\mathbb F_p^{*}$
. -
(b) If
 $\overline {\rho }_{E,p}(I_\lambda )$
is divisible by
$\overline {\rho }_{E,p}(I_\lambda )$
is divisible by
 $3$
, then there exists an element
$3$
, then there exists an element
 $g \in \overline {\rho }_{E,p}(I_\lambda )$
which has order
$g \in \overline {\rho }_{E,p}(I_\lambda )$
which has order
 $3$
, and hence
$3$
, and hence
 $\lambda (g) \in {\mathbb F}_{p^2}^\times $
has order
$\lambda (g) \in {\mathbb F}_{p^2}^\times $
has order
 $3$
. Moreover, note that
$3$
. Moreover, note that
 $\chi _p$
is unramified at p. Therefore,
$\chi _p$
is unramified at p. Therefore,
 $\chi _p(g)=\lambda ^{p+1}(g)=1$
, which implies that
$\chi _p(g)=\lambda ^{p+1}(g)=1$
, which implies that
 $3|p+1$
.
$3|p+1$
.
-
-
(3) When K is totally real, then the absolute Galois group
 $G_K$
contains a complex conjugation. The image of this complex conjugation under
$G_K$
contains a complex conjugation. The image of this complex conjugation under
 $\overline {\rho }_{E,p}$
is similar to
$\overline {\rho }_{E,p}$
is similar to
 $\begin {pmatrix} 1 & 0 \\ 0 & -1 \end {pmatrix}$
, which implies that if
$\begin {pmatrix} 1 & 0 \\ 0 & -1 \end {pmatrix}$
, which implies that if
 $\overline {\rho }_{E,p}$
is irreducible, then it is absolutely irreducible.
$\overline {\rho }_{E,p}$
is irreducible, then it is absolutely irreducible.
The following theorem of Larson and Vaintrob is used in the proof of the above corollary.
Theorem 3.11 [Reference Larson and Vaintrob22, Theorem 1]
Let K be a number field. There exists a finite set of primes
![]() $M_K$
, depending only on K, such that, for any prime
$M_K$
, depending only on K, such that, for any prime
![]() $p \notin M_K$
and any elliptic curve
$p \notin M_K$
and any elliptic curve
![]() $E/K$
for which
$E/K$
for which
![]() $\overline {\rho }_{E,p} \otimes \overline {\mathbb F}_p$
is conjugate to
$\overline {\rho }_{E,p} \otimes \overline {\mathbb F}_p$
is conjugate to
 $\begin {pmatrix} \lambda & * \\ 0 & \lambda ' \end {pmatrix}$
where
$\begin {pmatrix} \lambda & * \\ 0 & \lambda ' \end {pmatrix}$
where
![]() $\lambda , \lambda ' :G \rightarrow \mathbb {F}_p^\times $
are characters, one of the following happens.
$\lambda , \lambda ' :G \rightarrow \mathbb {F}_p^\times $
are characters, one of the following happens.
-
(1) There exists an elliptic curve
 $E'/K$
with CM, whose CM field is contained in K, with
$E'/K$
with CM, whose CM field is contained in K, with
 $\overline {\rho }_{E',p} \otimes \overline {\mathbb F}_p$
is conjugate to
$\overline {\rho }_{E',p} \otimes \overline {\mathbb F}_p$
is conjugate to
 $\begin {pmatrix} \theta & * \\ 0 & \theta ' \end {pmatrix}$
and such that
$\begin {pmatrix} \theta & * \\ 0 & \theta ' \end {pmatrix}$
and such that
 $\theta ^{12}=\lambda ^{12}.$
$\theta ^{12}=\lambda ^{12}.$
-
(2) The Generalized Riemann Hypothesis (GRH) fails for
 $K={\mathbb Q}(\sqrt {-p})$
and
$K={\mathbb Q}(\sqrt {-p})$
and
 $\theta ^{12}=\chi _p^6$
. Moreover, in this case,
$\theta ^{12}=\chi _p^6$
. Moreover, in this case,
 $\overline {\rho }_{E',p}$
is already reducible over
$\overline {\rho }_{E',p}$
is already reducible over
 ${\mathbb F}_p$
and
${\mathbb F}_p$
and
 $p \equiv 3 \ \pmod 4.$
$p \equiv 3 \ \pmod 4.$
4 Proof of Theorem 1.1
In this section, we will prove Theorem 1.1.
Let K be a number field with
![]() $h^{+}_K=1$
satisfying Conjectures 2.2 and 2.3 and containing
$h^{+}_K=1$
satisfying Conjectures 2.2 and 2.3 and containing
![]() ${\mathbb Q}(\zeta _{3})$
where
${\mathbb Q}(\zeta _{3})$
where
![]() $\zeta _{3}$
is a primitive third root of unity. Assume that
$\zeta _{3}$
is a primitive third root of unity. Assume that
![]() $\lambda $
is the only prime of K above
$\lambda $
is the only prime of K above
![]() $3$
. Let
$3$
. Let
![]() $B_K$
be as in Theorem 3.1, and let
$B_K$
be as in Theorem 3.1, and let
![]() $(a,b,c)\in W_K$
be a nontrivial solution to the Fermat equation with signature
$(a,b,c)\in W_K$
be a nontrivial solution to the Fermat equation with signature
![]() $(p,p,3)$
given in (1.1). We now apply Theorem 3.1 and obtain an elliptic curve
$(p,p,3)$
given in (1.1). We now apply Theorem 3.1 and obtain an elliptic curve
![]() $E'/K$
having a K-rational point of order
$E'/K$
having a K-rational point of order
![]() $3$
and (potentially) good reduction away from
$3$
and (potentially) good reduction away from
![]() $\lambda $
with j-invariant
$\lambda $
with j-invariant
![]() $j'$
satisfying
$j'$
satisfying
![]() $v_{\lambda }(j')<0$
. However, by Theorem 4.1 applied with
$v_{\lambda }(j')<0$
. However, by Theorem 4.1 applied with
![]() $\ell =3$
, there is no such an elliptic curve, which gives us a contradiction.
$\ell =3$
, there is no such an elliptic curve, which gives us a contradiction.
Theorem 4.1 [Reference Freitas, Kraus and Siksek11, Theorem 1]
Let
![]() $\ell $
be a rational prime. Let K be a number field satisfying the following conditions:
$\ell $
be a rational prime. Let K be a number field satisfying the following conditions:
-
•
 ${\mathbb Q}(\zeta _{\ell }) \subset K$
, where
${\mathbb Q}(\zeta _{\ell }) \subset K$
, where
 $\zeta _{\ell }$
is a primitive
$\zeta _{\ell }$
is a primitive
 $\ell $
th root of unity;
$\ell $
th root of unity; -
• K has a unique prime
 $\lambda $
above
$\lambda $
above
 $\ell $
;
$\ell $
; -
•
 $gcd(h_K^+,\ell (\ell -1))=1$
, where
$gcd(h_K^+,\ell (\ell -1))=1$
, where
 $h_K^+$
is the narrow class number of K.
$h_K^+$
is the narrow class number of K.
Then there is no elliptic curve
![]() $E/K$
with a K-rational
$E/K$
with a K-rational
![]() $\ell $
-isogeny, good reduction away from
$\ell $
-isogeny, good reduction away from
![]() $\lambda $
, potentially multiplicative reduction at
$\lambda $
, potentially multiplicative reduction at
![]() $\lambda $
.
$\lambda $
.
Remark 4.2 Since we assume that
![]() ${\mathbb Q}(\zeta _{3}) \subset K$
, the triple
${\mathbb Q}(\zeta _{3}) \subset K$
, the triple
![]() $(\zeta _3, \zeta ^2_3,1)$
is a nontrivial solution to equation (1.1) in
$(\zeta _3, \zeta ^2_3,1)$
is a nontrivial solution to equation (1.1) in
![]() $\mathcal O_K$
. However, as
$\mathcal O_K$
. However, as
![]() $\zeta _3$
is a unit in
$\zeta _3$
is a unit in
![]() $\mathcal {O}_K$
, the prime
$\mathcal {O}_K$
, the prime
![]() $\lambda $
does not divide
$\lambda $
does not divide
![]() $(\zeta _3)=\mathcal {O}_K$
, so
$(\zeta _3)=\mathcal {O}_K$
, so
![]() $(\zeta _3, \zeta ^2_3,1) \not \in W_K$
.
$(\zeta _3, \zeta ^2_3,1) \not \in W_K$
.
4.1 Numerical examples
Let
![]() $\mathcal {F}_n$
denote the set of number fields of degree n and class number
$\mathcal {F}_n$
denote the set of number fields of degree n and class number
![]() $1$
with discriminant less than
$1$
with discriminant less than
![]() $D_n$
, where
$D_n$
, where
![]() $D_n$
is
$D_n$
is
![]() $10^8$
if
$10^8$
if
![]() $n=4,6,8$
and
$n=4,6,8$
and
![]() $10^{16}$
if
$10^{16}$
if
![]() $n=10,12$
. Let
$n=10,12$
. Let
![]() $\mathcal {K}_n$
denote the subset of
$\mathcal {K}_n$
denote the subset of
![]() $\mathcal {F}_n$
such that if
$\mathcal {F}_n$
such that if
![]() $K\in \mathcal {K}_n$
, then K satisfies the following:
$K\in \mathcal {K}_n$
, then K satisfies the following:
-
•
 ${\mathbb Q}(\zeta _3)\subset K$
;
${\mathbb Q}(\zeta _3)\subset K$
; -
• the narrow class number of K is
 $1$
;
$1$
; -
• there is only one prime ideal of K lying above
 $3$
.
$3$
.
We computed the complete sets
![]() $\mathcal {F}_n$
and
$\mathcal {F}_n$
and
![]() $ \mathcal {K}_n$
for
$ \mathcal {K}_n$
for
![]() $n=4,6,8,10,12$
in the John Jones Number Field Database [Reference Jones and Roberts15]. The cardinalities of these sets are given in Table 1, and details can be found online at https://sites.google.com/view/erman-isik/research?authuser=0.
$n=4,6,8,10,12$
in the John Jones Number Field Database [Reference Jones and Roberts15]. The cardinalities of these sets are given in Table 1, and details can be found online at https://sites.google.com/view/erman-isik/research?authuser=0.
It then follows from Theorem 1.1 that, for any K that belongs to
![]() $\mathcal {K}_n$
, the asymptotic FLT holds for
$\mathcal {K}_n$
, the asymptotic FLT holds for
![]() $W_K$
.
$W_K$
.
5 Proof of Theorem 1.2
In this section, we will prove Theorem 1.2. One of the main steps toward the proof is to lift mod p eigenforms to complex ones. Recall that it follows from Proposition 2.1 that there is a constant
![]() $B({\mathfrak N})$
such that, for
$B({\mathfrak N})$
such that, for
![]() $p>B({\mathfrak N})$
, all weight-two, mod p eigenforms lift to complex ones. However, we want to make this bound explicit for the fields we consider for Theorem 1.2. Before the proof of Theorem 1.2, we will state the key point to overcome this difficulty. Note that our approach follows closely [Reference Ţurcaş31, Section 2] and [Reference Şengün and Siksek27, Sections 2 and 3].
$p>B({\mathfrak N})$
, all weight-two, mod p eigenforms lift to complex ones. However, we want to make this bound explicit for the fields we consider for Theorem 1.2. Before the proof of Theorem 1.2, we will state the key point to overcome this difficulty. Note that our approach follows closely [Reference Ţurcaş31, Section 2] and [Reference Şengün and Siksek27, Sections 2 and 3].
Let K be a number field with the integer ring
![]() ${\mathcal O}_{K}$
, and let
${\mathcal O}_{K}$
, and let
![]() ${\mathfrak N}$
be an ideal of
${\mathfrak N}$
be an ideal of
![]() ${\mathcal O}_{K}$
. Assume that p is a rational prime unramified in K and relatively prime to
${\mathcal O}_{K}$
. Assume that p is a rational prime unramified in K and relatively prime to
![]() ${\mathfrak N}$
. Consider the following short exact sequence given by a multiplication-by-p map
${\mathfrak N}$
. Consider the following short exact sequence given by a multiplication-by-p map
where
![]() $\mathbb {Z}_{(p)}$
denotes the ring of rational numbers with denominators prime to p.
$\mathbb {Z}_{(p)}$
denotes the ring of rational numbers with denominators prime to p.
This exact sequence gives rise to a long exact sequence on the cohomology groups from which we can extract the following short exact sequence:
where
![]() $H^2(Y_0({\mathfrak N}), \mathbb {Z}_{(p)})[p]$
denotes the p-torsion subgroup of
$H^2(Y_0({\mathfrak N}), \mathbb {Z}_{(p)})[p]$
denotes the p-torsion subgroup of
![]() $H^2(Y_0({\mathfrak N}), \mathbb {Z}_{(p)})$
. Hence, we deduce that the p-torsion subgroup of
$H^2(Y_0({\mathfrak N}), \mathbb {Z}_{(p)})$
. Hence, we deduce that the p-torsion subgroup of
![]() $H^2(Y_0({\mathfrak N}),\mathbb {Z}_{(p)})$
is trivial if and only if the reduction map from
$H^2(Y_0({\mathfrak N}),\mathbb {Z}_{(p)})$
is trivial if and only if the reduction map from
![]() $H^1(Y_0({\mathfrak N}),\mathbb {Z}_{(p)})$
to
$H^1(Y_0({\mathfrak N}),\mathbb {Z}_{(p)})$
to
![]() $H^1(Y_0({\mathfrak N}),\mathbb {F}_p)$
is surjective. As explained in [Reference Şengün and Siksek27, Reference Ţurcaş31], we see that, for primes
$H^1(Y_0({\mathfrak N}),\mathbb {F}_p)$
is surjective. As explained in [Reference Şengün and Siksek27, Reference Ţurcaş31], we see that, for primes
![]() $p>3$
, if the group
$p>3$
, if the group
![]() $H^2(\Gamma _0({\mathfrak N}), \mathbb {Z}_{(p)})$
has a nontrivial p-torsion element, then
$H^2(\Gamma _0({\mathfrak N}), \mathbb {Z}_{(p)})$
has a nontrivial p-torsion element, then
![]() $\Gamma _0({\mathfrak N})^{\mathrm {ab}}$
will have a p-torsion as well. If
$\Gamma _0({\mathfrak N})^{\mathrm {ab}}$
will have a p-torsion as well. If
![]() $H^2(Y_0({\mathfrak N}), \mathbb {Z}_{(p)})$
has only trivial p-torsion, then we deduce that the map
$H^2(Y_0({\mathfrak N}), \mathbb {Z}_{(p)})$
has only trivial p-torsion, then we deduce that the map
is surjective. Therefore, any Hecke eigenvector in
![]() $H^1(Y_0({\mathfrak N}), \mathbb {F}_p)$
comes from such an eigenvector in
$H^1(Y_0({\mathfrak N}), \mathbb {F}_p)$
comes from such an eigenvector in
![]() $H^1(Y_0({\mathfrak N}), \mathbb {Z}_{(p)})\otimes \mathbb {F}_p$
. We can now utilize a lifting lemma of Ash and Stevens [Reference Ash and Stevens1, Proposition 1.2.2] to deduce that, by fixing an embedding
$H^1(Y_0({\mathfrak N}), \mathbb {Z}_{(p)})\otimes \mathbb {F}_p$
. We can now utilize a lifting lemma of Ash and Stevens [Reference Ash and Stevens1, Proposition 1.2.2] to deduce that, by fixing an embedding
![]() $\overline {\mathbb {Q}} \hookrightarrow \mathbb {C} $
, we can regard a cohomology class in
$\overline {\mathbb {Q}} \hookrightarrow \mathbb {C} $
, we can regard a cohomology class in
![]() $H^1(Y_0({\mathfrak N}), \mathbb {Z}_{(p)})$
as a class in
$H^1(Y_0({\mathfrak N}), \mathbb {Z}_{(p)})$
as a class in
![]() $H^1(Y_0({\mathfrak N}), \mathbb {C})$
.
$H^1(Y_0({\mathfrak N}), \mathbb {C})$
.
The existence of an eigenform (complex or mod p) is equivalent to the existence of a cohomology class in the corresponding cohomology group that is a simultaneous eigenvector for the Hecke operators such that its eigenvalues match the values of the eigenform. With this interpretation, we see that, for
![]() $p>3$
, the mod p eigenforms lift to complex eigenforms whenever the abelianization
$p>3$
, the mod p eigenforms lift to complex eigenforms whenever the abelianization
![]() $\Gamma _0({\mathfrak N})^{\mathrm {ab}}$
has only trivial p-torsion element.
$\Gamma _0({\mathfrak N})^{\mathrm {ab}}$
has only trivial p-torsion element.
5.1 Proof of Theorem 1.2
Let
![]() $K=\mathbb {Q}(\sqrt {-d})$
with
$K=\mathbb {Q}(\sqrt {-d})$
with
![]() $d\in \{1,7,19,43,67\}$
, and let
$d\in \{1,7,19,43,67\}$
, and let
![]() $\lambda $
denote the prime ideal of K lying above
$\lambda $
denote the prime ideal of K lying above
![]() $3$
. Suppose that
$3$
. Suppose that
![]() $(a,b,c)\in \mathcal {O}_K^3$
is a nontrivial primitive solution to equation (1.1).
$(a,b,c)\in \mathcal {O}_K^3$
is a nontrivial primitive solution to equation (1.1).
Let
![]() $\overline {\rho }_{E,p}$
be the residual Galois representation induced by the action of
$\overline {\rho }_{E,p}$
be the residual Galois representation induced by the action of
![]() $G_K$
on
$G_K$
on
![]() $E[p]$
. We want to apply Conjecture 2.2 to
$E[p]$
. We want to apply Conjecture 2.2 to
![]() $\overline {\rho }_{E,p}$
. Note that in order to do this, we need
$\overline {\rho }_{E,p}$
. Note that in order to do this, we need
![]() $\overline {\rho }_{E,p}$
to be absolutely irreducible. It follows from Corollary 3.10 that
$\overline {\rho }_{E,p}$
to be absolutely irreducible. It follows from Corollary 3.10 that
![]() $\overline {\rho }_{E,p}$
is absolutely irreducible under the assumptions of Theorem 1.2 and hence satisfies the hypotheses of Conjecture 2.2. This will be explained in Cases I and II below. For now, let us assume that Conjecture 2.2 is applicable. Applying this conjecture, we deduce that there exists a weight-two, mod p eigenform
$\overline {\rho }_{E,p}$
is absolutely irreducible under the assumptions of Theorem 1.2 and hence satisfies the hypotheses of Conjecture 2.2. This will be explained in Cases I and II below. For now, let us assume that Conjecture 2.2 is applicable. Applying this conjecture, we deduce that there exists a weight-two, mod p eigenform
![]() $\theta $
over K of level
$\theta $
over K of level
![]() ${\mathfrak N}_E$
such that, for all primes
${\mathfrak N}_E$
such that, for all primes
![]() ${\mathfrak q}$
coprime to
${\mathfrak q}$
coprime to
![]() $p{\mathfrak N}_E$
, we have
$p{\mathfrak N}_E$
, we have
where
![]() $T_{{\mathfrak q}}$
denotes the Hecke operator at
$T_{{\mathfrak q}}$
denotes the Hecke operator at
![]() ${\mathfrak q}$
.
${\mathfrak q}$
.
Recall that
![]() ${\mathfrak N}_E$
denotes the Serre conductor of the residual representation
${\mathfrak N}_E$
denotes the Serre conductor of the residual representation
![]() $\overline {\rho }_{E,p}$
, which is a power of
$\overline {\rho }_{E,p}$
, which is a power of
![]() $\lambda $
. We now aim to lift this mod p Bianchi modular form to a complex one.
$\lambda $
. We now aim to lift this mod p Bianchi modular form to a complex one.
We compute the abelianizations
![]() $\Gamma _0({\mathfrak N}_E)^{\mathrm {ab}}$
implementing the algorithm of Şengün [Reference Şengün26]. One can access to the relevant Magma codes online at https://warwick.ac.uk/fac/sci/maths/people/staff/turcas/fermatprog. The results of the algorithm can be found at https://sites.google.com/view/erman-isik/research?authuser=0. We record here the primes
$\Gamma _0({\mathfrak N}_E)^{\mathrm {ab}}$
implementing the algorithm of Şengün [Reference Şengün26]. One can access to the relevant Magma codes online at https://warwick.ac.uk/fac/sci/maths/people/staff/turcas/fermatprog. The results of the algorithm can be found at https://sites.google.com/view/erman-isik/research?authuser=0. We record here the primes
![]() $\ell $
that appear as orders of torsion elements of
$\ell $
that appear as orders of torsion elements of
![]() $\Gamma _0({\mathfrak N}_E)^{\mathrm {ab}}$
for each number field in Table 2.
$\Gamma _0({\mathfrak N}_E)^{\mathrm {ab}}$
for each number field in Table 2.
Assume that
![]() $\ell _K$
is the largest prime in Table 2 related to the number field K, and that
$\ell _K$
is the largest prime in Table 2 related to the number field K, and that
![]() $p> \ell _K$
. It then follows that the p-torsion subgroups of
$p> \ell _K$
. It then follows that the p-torsion subgroups of
![]() $\Gamma _0({\mathfrak N}_E)^{\mathrm {ab}}$
are all trivial, so the mod p eigenforms must lift to complex ones. The procedure explained at the beginning of Section 5 together with Conjecture 2.2 implies that there exists a (complex) Bianchi modular form
$\Gamma _0({\mathfrak N}_E)^{\mathrm {ab}}$
are all trivial, so the mod p eigenforms must lift to complex ones. The procedure explained at the beginning of Section 5 together with Conjecture 2.2 implies that there exists a (complex) Bianchi modular form
![]() ${\mathfrak f}$
over K of level
${\mathfrak f}$
over K of level
![]() ${\mathfrak N}_E$
such that, for all prime ideals
${\mathfrak N}_E$
such that, for all prime ideals
![]() $\mathfrak {q}$
coprime to
$\mathfrak {q}$
coprime to
![]() $p{\mathfrak N}_E$
, we have
$p{\mathfrak N}_E$
, we have
where
![]() ${\mathfrak p}$
is a prime ideal of
${\mathfrak p}$
is a prime ideal of
![]() $\mathbb {Q}_{\mathfrak f}$
lying above p and
$\mathbb {Q}_{\mathfrak f}$
lying above p and
![]() $\mathbb {Q}_{\mathfrak f}$
is the number field generated by the eigenvalues. Let us denote this relation by
$\mathbb {Q}_{\mathfrak f}$
is the number field generated by the eigenvalues. Let us denote this relation by
![]() $\overline {\rho }_{E,p}\sim \overline {\rho }_{{\mathfrak f},{\mathfrak p}}$
.
$\overline {\rho }_{E,p}\sim \overline {\rho }_{{\mathfrak f},{\mathfrak p}}$
.
Recall that the constants
![]() $C_K$
and
$C_K$
and
![]() $M_K$
were defined in Proposition 3.9 and in Corollary 3.10.
$M_K$
were defined in Proposition 3.9 and in Corollary 3.10.
5.2 Case I
Assume that the prime ideal
![]() $\lambda $
of K lying above
$\lambda $
of K lying above
![]() $3$
divides b. Note that, in this case, the associated Frey curve is semistable by Lemma 2.4. By Proposition 3.9,
$3$
divides b. Note that, in this case, the associated Frey curve is semistable by Lemma 2.4. By Proposition 3.9,
![]() $\overline {\rho }_{E,p}$
is irreducible when
$\overline {\rho }_{E,p}$
is irreducible when
![]() $p>C_K$
. By Part 1 of Corollary 3.10,
$p>C_K$
. By Part 1 of Corollary 3.10,
![]() $\overline {\rho }_{E,p}$
is absolutely irreducible if it is irreducible. Therefore, Conjecture 2.2 is applicable to
$\overline {\rho }_{E,p}$
is absolutely irreducible if it is irreducible. Therefore, Conjecture 2.2 is applicable to
![]() $\overline {\rho }_{E,p}$
. When we apply Conjecture 2.2 and the lifting argument above, we see that the corresponding Bianchi modular form
$\overline {\rho }_{E,p}$
. When we apply Conjecture 2.2 and the lifting argument above, we see that the corresponding Bianchi modular form
![]() ${\mathfrak f}$
is of level
${\mathfrak f}$
is of level
![]() $1 $
or
$1 $
or
![]() $\lambda $
. Since there are no Bianchi newforms at these levels over K, it follows that Theorem 1.2 holds true for
$\lambda $
. Since there are no Bianchi newforms at these levels over K, it follows that Theorem 1.2 holds true for
![]() $p>\mathrm {max} \{\ell _K, C_K\}$
. This proves Case I of Theorem 1.2.
$p>\mathrm {max} \{\ell _K, C_K\}$
. This proves Case I of Theorem 1.2.
5.3 Case II
Assume now that
![]() $\lambda $
does not divide b.
$\lambda $
does not divide b.
In this case, we do not have the absolute irreducibility of
![]() $\overline {\rho }_{E,p}$
for all primes p as illustrated in Corollary 3.10. Therefore we need the restrictions in the statement of Part II of Theorem 1.2, i.e.,
$\overline {\rho }_{E,p}$
for all primes p as illustrated in Corollary 3.10. Therefore we need the restrictions in the statement of Part II of Theorem 1.2, i.e.,
![]() $p \equiv 3 \mod 4$
and p splits in K. Under these restrictions and when
$p \equiv 3 \mod 4$
and p splits in K. Under these restrictions and when
![]() $p> \mathrm {max}\{C_K, M_K\}$
,
$p> \mathrm {max}\{C_K, M_K\}$
,
![]() $\overline {\rho }_{E,p}$
is absolutely irreducible by Corollary 3.10. We also need
$\overline {\rho }_{E,p}$
is absolutely irreducible by Corollary 3.10. We also need
![]() $p> \ell _K $
to lift the mod p eigenforms to complex ones as explained above. Therefore, from now on, we assume that
$p> \ell _K $
to lift the mod p eigenforms to complex ones as explained above. Therefore, from now on, we assume that
![]() $p> B_K=\mathrm {max}\{C_K, M_K,\ell _K\}$
.
$p> B_K=\mathrm {max}\{C_K, M_K,\ell _K\}$
.
Recall that, in this case, the associated Frey curve is semistable away from
![]() $\lambda $
and the power of
$\lambda $
and the power of
![]() $\lambda $
in the conductor of E is
$\lambda $
in the conductor of E is
![]() $2$
or
$2$
or
![]() $3$
by Lemma 2.4. Then the corresponding Bianchi modular form is of level dividing
$3$
by Lemma 2.4. Then the corresponding Bianchi modular form is of level dividing
![]() $\lambda ^{3}$
.
$\lambda ^{3}$
.
Lemma 5.1 Let us fix a prime ideal
![]() $\mathfrak {q} \neq \lambda $
of K, and let
$\mathfrak {q} \neq \lambda $
of K, and let
![]() ${\mathfrak f}$
be a newform of level dividing
${\mathfrak f}$
be a newform of level dividing
![]() $\lambda ^{3}$
. Define the following set:
$\lambda ^{3}$
. Define the following set:
If
![]() $\overline {\rho }_{E,p}\sim \overline {\rho }_{{\mathfrak f},{\mathfrak p}}$
, where
$\overline {\rho }_{E,p}\sim \overline {\rho }_{{\mathfrak f},{\mathfrak p}}$
, where
![]() ${\mathfrak p}$
is the prime ideal of
${\mathfrak p}$
is the prime ideal of
![]() $\mathbb {Q}_{{\mathfrak f}}$
lying above p, then
$\mathbb {Q}_{{\mathfrak f}}$
lying above p, then
![]() ${\mathfrak p}$
divides
${\mathfrak p}$
divides
Proof If
![]() $\mathfrak {q}|p$
, then
$\mathfrak {q}|p$
, then
![]() $\operatorname {\mbox { Norm}}(\mathfrak {q})$
is a power of p. Now, assume that
$\operatorname {\mbox { Norm}}(\mathfrak {q})$
is a power of p. Now, assume that
![]() $\mathfrak {q}$
does not divide p. Then the Frey curve E has semistable reduction at
$\mathfrak {q}$
does not divide p. Then the Frey curve E has semistable reduction at
![]() $\mathfrak {q}$
. If it has a good reduction, then we have
$\mathfrak {q}$
. If it has a good reduction, then we have
Note that, by Lemma 2.4, the Frey curve E, given in (2.3), has a
![]() $3$
-torsion point, so
$3$
-torsion point, so
![]() $3$
divides
$3$
divides
![]() $\#E(\mathbb {F}_{\mathfrak {q}})=\operatorname {\mbox { Norm}}(\mathfrak {q})+1=a_{\mathfrak {q}}(E)$
. By the Hasse–Weil bound, we know that
$\#E(\mathbb {F}_{\mathfrak {q}})=\operatorname {\mbox { Norm}}(\mathfrak {q})+1=a_{\mathfrak {q}}(E)$
. By the Hasse–Weil bound, we know that
![]() $|a_{\mathfrak {q}}(E)|\leq 2\sqrt {\operatorname {\mbox { Norm}}(\mathfrak {q})}$
. So
$|a_{\mathfrak {q}}(E)|\leq 2\sqrt {\operatorname {\mbox { Norm}}(\mathfrak {q})}$
. So
![]() $a_{\mathfrak {q}}(E)$
belongs to the finite set
$a_{\mathfrak {q}}(E)$
belongs to the finite set
![]() $\mathcal {A}({\mathfrak q})$
. Finally, suppose that E has multiplicative reduction at
$\mathcal {A}({\mathfrak q})$
. Finally, suppose that E has multiplicative reduction at
![]() $\mathfrak {q}$
. Then, by comparing the traces of the images of Frobenius at
$\mathfrak {q}$
. Then, by comparing the traces of the images of Frobenius at
![]() $\mathfrak {q}$
under
$\mathfrak {q}$
under
![]() $\overline {\rho }_{E,p}$
, we have
$\overline {\rho }_{E,p}$
, we have
It then follows that
![]() ${\mathfrak p}$
divides
${\mathfrak p}$
divides
![]() $(\operatorname {\mbox { Norm}}(\mathfrak {q})+1)^2-\mathfrak {f}(T_{\mathfrak {q}})^2$
. Hence,
$(\operatorname {\mbox { Norm}}(\mathfrak {q})+1)^2-\mathfrak {f}(T_{\mathfrak {q}})^2$
. Hence,
![]() $\mathfrak {p}$
divides
$\mathfrak {p}$
divides
![]() $B_{{\mathfrak f},\mathfrak {q}}$
.
$B_{{\mathfrak f},\mathfrak {q}}$
.
Using Magma, we computed the cuspidal newforms at the predicted levels, the fields
![]() $\mathbb {Q}_{\mathfrak f}$
, and eigenvalues
$\mathbb {Q}_{\mathfrak f}$
, and eigenvalues
![]() ${\mathfrak f}(T_{\mathfrak q})$
at the prime ideals
${\mathfrak f}(T_{\mathfrak q})$
at the prime ideals
![]() ${\mathfrak q}$
of norm less that
${\mathfrak q}$
of norm less that
![]() $50$
for each imaginary quadratic number field
$50$
for each imaginary quadratic number field
![]() $K=\mathbb {Q}(\sqrt {-d})$
with
$K=\mathbb {Q}(\sqrt {-d})$
with
![]() $d\in \{1,7,19,43,67\}$
. For each modular form
$d\in \{1,7,19,43,67\}$
. For each modular form
![]() ${\mathfrak f}$
of level dividing
${\mathfrak f}$
of level dividing
![]() $\lambda ^3$
, we computed the ideal
$\lambda ^3$
, we computed the ideal
where S denotes the set of prime ideals
![]() ${\mathfrak q}\neq \lambda $
of K of norm less than
${\mathfrak q}\neq \lambda $
of K of norm less than
![]() $50$
. The algorithm that we implemented and the results for the following fields can be found online at https://sites.google.com/view/erman-isik/research?authuser=0.
$50$
. The algorithm that we implemented and the results for the following fields can be found online at https://sites.google.com/view/erman-isik/research?authuser=0.
Set
![]() $C_{\mathfrak f}:=\mathrm {Norm}_{\mathbb {Q}_{\mathfrak f}/\mathbb {Q}}(B_{\mathfrak f})$
. It then follows from Lemma 5.1 that if
$C_{\mathfrak f}:=\mathrm {Norm}_{\mathbb {Q}_{\mathfrak f}/\mathbb {Q}}(B_{\mathfrak f})$
. It then follows from Lemma 5.1 that if
![]() $\overline {\rho }_{E,p}\sim \overline {\rho }_{{\mathfrak f},{\mathfrak p}}$
, then p divides
$\overline {\rho }_{E,p}\sim \overline {\rho }_{{\mathfrak f},{\mathfrak p}}$
, then p divides
![]() $C_{\mathfrak f}$
. Note that it is possible to find
$C_{\mathfrak f}$
. Note that it is possible to find
![]() $C_{\mathfrak f}=0$
. In this case, we need to deal with such modular forms individually.
$C_{\mathfrak f}=0$
. In this case, we need to deal with such modular forms individually.
We say that an elliptic curve
![]() $C/K$
of conductor
$C/K$
of conductor
![]() $\mathcal {N}\subset \mathcal {O}_K$
corresponds to a cuspidal Bianchi modular form F for
$\mathcal {N}\subset \mathcal {O}_K$
corresponds to a cuspidal Bianchi modular form F for
![]() $\Gamma _0(\mathcal {N})$
, if the L-series
$\Gamma _0(\mathcal {N})$
, if the L-series
![]() $L(C/K,s)$
attached to
$L(C/K,s)$
attached to
![]() $C/K$
is equal to the Mellin transform
$C/K$
is equal to the Mellin transform
![]() $L(F,s)$
of F.
$L(F,s)$
of F.
-
(1) If
 $K=\mathbb Q (i)$
, then there is no Bianchi modular form at level
$K=\mathbb Q (i)$
, then there is no Bianchi modular form at level
 $\lambda ^\epsilon $
where
$\lambda ^\epsilon $
where
 $\epsilon =1,2$
. There is only one modular form at level
$\epsilon =1,2$
. There is only one modular form at level
 $\lambda ^3$
. For this modular form, we have
$\lambda ^3$
. For this modular form, we have
 $C_{\mathfrak {f}}=0$
and
$C_{\mathfrak {f}}=0$
and
 $\mathbb {Q}_{\mathfrak f}=\mathbb {Q}$
. The elliptic curves in the isogeny class given in the LMFDB label 2.0.4.1-729.1-a correspond to this form. All the elliptic curves in this class are defined over
$\mathbb {Q}_{\mathfrak f}=\mathbb {Q}$
. The elliptic curves in the isogeny class given in the LMFDB label 2.0.4.1-729.1-a correspond to this form. All the elliptic curves in this class are defined over
 $\mathbb {Q}$
and have CM.
$\mathbb {Q}$
and have CM. -
(2) If
 $K=\mathbb Q(\sqrt {-7})$
, then there is no Bianchi modular form at level
$K=\mathbb Q(\sqrt {-7})$
, then there is no Bianchi modular form at level
 $\lambda ^\epsilon $
with
$\lambda ^\epsilon $
with
 $\epsilon =1,2$
. There are three modular forms at level
$\epsilon =1,2$
. There are three modular forms at level
 $\lambda ^3$
. For one of these forms,
$\lambda ^3$
. For one of these forms,
 $C_{\mathfrak f}$
is divisible by
$C_{\mathfrak f}$
is divisible by
 $2$
and
$2$
and
 $5$
, and for the other,
$5$
, and for the other,
 $C_{{\mathfrak f}}$
is divisible by
$C_{{\mathfrak f}}$
is divisible by
 $2$
and
$2$
and
 $7$
. For the third modular form, we get
$7$
. For the third modular form, we get
 $C_{\mathfrak f}=0$
, and
$C_{\mathfrak f}=0$
, and
 $\mathbb {Q}_{\mathfrak f}=\mathbb {Q}$
. The elliptic curves in the isogeny class given in the LMFDB label 2.0.7.1-729.1-a correspond to this cuspidal form. All the elliptic curves in this class are defined over
$\mathbb {Q}_{\mathfrak f}=\mathbb {Q}$
. The elliptic curves in the isogeny class given in the LMFDB label 2.0.7.1-729.1-a correspond to this cuspidal form. All the elliptic curves in this class are defined over
 $\mathbb {Q}$
and have CM.
$\mathbb {Q}$
and have CM. -
(3) If
 $K=\mathbb Q(\sqrt {-19})$
, then there is no Bianchi modular form at level
$K=\mathbb Q(\sqrt {-19})$
, then there is no Bianchi modular form at level
 $\lambda $
. There are two Bianchi modular forms at level
$\lambda $
. There are two Bianchi modular forms at level
 $\lambda ^2$
. For both of these forms,
$\lambda ^2$
. For both of these forms,
 $C_{\mathfrak f}$
is divisible by
$C_{\mathfrak f}$
is divisible by
 $2$
. There are three modular forms at level
$2$
. There are three modular forms at level
 $\lambda ^3$
. For one of these forms,
$\lambda ^3$
. For one of these forms,
 $C_{\mathfrak f}$
is divisible by
$C_{\mathfrak f}$
is divisible by
 $7$
, and for the other,
$7$
, and for the other,
 $C_{{\mathfrak f}}$
is divisible by
$C_{{\mathfrak f}}$
is divisible by
 $2$
and
$2$
and
 $17$
. For the third modular form, we get
$17$
. For the third modular form, we get
 $C_{\mathfrak f}=0$
and
$C_{\mathfrak f}=0$
and
 $\mathbb {Q}_{\mathfrak f}=\mathbb {Q}$
. The elliptic curves in the isogeny class given in the LMFDB label 2.0.19.1-729.1-a correspond to this modular form. All the elliptic curves in this class are defined over
$\mathbb {Q}_{\mathfrak f}=\mathbb {Q}$
. The elliptic curves in the isogeny class given in the LMFDB label 2.0.19.1-729.1-a correspond to this modular form. All the elliptic curves in this class are defined over
 $\mathbb {Q}$
and have CM.
$\mathbb {Q}$
and have CM. -
(4) If
 $K=\mathbb Q(\sqrt {-43})$
, then there is no Bianchi modular form at level
$K=\mathbb Q(\sqrt {-43})$
, then there is no Bianchi modular form at level
 $\lambda $
. There are two Bianchi modular forms at level
$\lambda $
. There are two Bianchi modular forms at level
 $\lambda ^2$
. For one of these forms,
$\lambda ^2$
. For one of these forms,
 $C_{\mathfrak f}$
is divisible by
$C_{\mathfrak f}$
is divisible by
 $2$
and
$2$
and
 $5$
, and for the other,
$5$
, and for the other,
 $C_{\mathfrak f}$
is a power of
$C_{\mathfrak f}$
is a power of
 $2$
. There are three modular forms at level
$2$
. There are three modular forms at level
 $\lambda ^3$
. For one of these modular forms,
$\lambda ^3$
. For one of these modular forms,
 $C_{\mathfrak f}$
is one, and for the other modular form,
$C_{\mathfrak f}$
is one, and for the other modular form,
 $C_{\mathfrak f}$
is divisible by
$C_{\mathfrak f}$
is divisible by
 $2$
and
$2$
and
 $23$
. For the third modular form, we get
$23$
. For the third modular form, we get
 $C_{\mathfrak f}=0$
, and
$C_{\mathfrak f}=0$
, and
 $\mathbb {Q}_{\mathfrak f}=\mathbb {Q}$
. The elliptic curves in the isogeny class given in the LMFDB label 2.0.43.1-729.1-a correspond to this Bianchi modular form. All the elliptic curves in this class are defined over
$\mathbb {Q}_{\mathfrak f}=\mathbb {Q}$
. The elliptic curves in the isogeny class given in the LMFDB label 2.0.43.1-729.1-a correspond to this Bianchi modular form. All the elliptic curves in this class are defined over
 $\mathbb {Q}$
and have CM.
$\mathbb {Q}$
and have CM. -
(5) If
 $K=\mathbb Q(\sqrt {-67})$
, then there is no Bianchi modular form at level
$K=\mathbb Q(\sqrt {-67})$
, then there is no Bianchi modular form at level
 $\lambda $
. There are two Bianchi modular forms at level
$\lambda $
. There are two Bianchi modular forms at level
 $\lambda ^2$
. For both of these forms,
$\lambda ^2$
. For both of these forms,
 $C_{\mathfrak f}$
is divisible by
$C_{\mathfrak f}$
is divisible by
 $2$
. At level
$2$
. At level
 $\lambda ^3$
, we find three modular forms. For one of these modular forms,
$\lambda ^3$
, we find three modular forms. For one of these modular forms,
 $C_{\mathfrak f}$
is one, and for the other,
$C_{\mathfrak f}$
is one, and for the other,
 $C_{\mathfrak f}$
is divisible by
$C_{\mathfrak f}$
is divisible by
 $11$
and
$11$
and
 $19$
. For the third modular form, we get
$19$
. For the third modular form, we get
 $C_{\mathfrak f}=0$
and
$C_{\mathfrak f}=0$
and
 $\mathbb {Q}_{\mathfrak f}=\mathbb {Q}$
. The elliptic curves in the isogeny class given in the LMFDB label 2.0.67.1-729.1-a correspond to this modular form. All the elliptic curves in this class are defined over
$\mathbb {Q}_{\mathfrak f}=\mathbb {Q}$
. The elliptic curves in the isogeny class given in the LMFDB label 2.0.67.1-729.1-a correspond to this modular form. All the elliptic curves in this class are defined over
 $\mathbb {Q}$
and have CM.
$\mathbb {Q}$
and have CM.
If
![]() $\overline {\rho }_{E,p}\sim \overline {\rho }_{{\mathfrak f},{\mathfrak p}}$
, then by Lemma 5.1 we have
$\overline {\rho }_{E,p}\sim \overline {\rho }_{{\mathfrak f},{\mathfrak p}}$
, then by Lemma 5.1 we have
![]() $p| C_{\mathfrak f}$
. Since
$p| C_{\mathfrak f}$
. Since
![]() $p>B_K$
and
$p>B_K$
and
![]() $B_K$
is large enough, the isomorphism
$B_K$
is large enough, the isomorphism
![]() $\overline {\rho }_{E,p}\sim \overline {\rho }_{{\mathfrak f},{\mathfrak p}}$
is impossible when
$\overline {\rho }_{E,p}\sim \overline {\rho }_{{\mathfrak f},{\mathfrak p}}$
is impossible when
![]() $C_{\mathfrak f}\neq 0$
. If
$C_{\mathfrak f}\neq 0$
. If
![]() $C_{\mathfrak f} =0$
, then the Bianchi modular forms correspond to elliptic curves defined over
$C_{\mathfrak f} =0$
, then the Bianchi modular forms correspond to elliptic curves defined over
![]() $\mathbb {Q}$
with CM. Let
$\mathbb {Q}$
with CM. Let
![]() $\overline {\rho }_{E',p}:G_K\rightarrow \mathrm {GL}_2(\mathbb {F}_p)$
denote the mod p Galois representation attached to
$\overline {\rho }_{E',p}:G_K\rightarrow \mathrm {GL}_2(\mathbb {F}_p)$
denote the mod p Galois representation attached to
![]() $E'$
, where
$E'$
, where
![]() $E'$
is an elliptic curve that corresponds to the Bianchi modular form with
$E'$
is an elliptic curve that corresponds to the Bianchi modular form with
![]() $C_{\mathfrak f}=0$
. Then, for all but finitely many primes
$C_{\mathfrak f}=0$
. Then, for all but finitely many primes
![]() $\mathfrak {q}\subset \mathcal {O}_K$
, we have
$\mathfrak {q}\subset \mathcal {O}_K$
, we have
![]() $\mathrm {Tr}(\overline {\rho }_{E,p}(\mathrm {Frob}_{\mathfrak {q}}))=\mathrm { Tr}(\overline {\rho }_{E',p}(\mathrm {Frob}_{\mathfrak {q}}))$
. Since the set of Frobenius elements is dense in
$\mathrm {Tr}(\overline {\rho }_{E,p}(\mathrm {Frob}_{\mathfrak {q}}))=\mathrm { Tr}(\overline {\rho }_{E',p}(\mathrm {Frob}_{\mathfrak {q}}))$
. Since the set of Frobenius elements is dense in
![]() $G_K$
and the representation
$G_K$
and the representation
![]() $\overline {\rho }_{E,p}$
is irreducible, it follows from Brauer–Nesbitt theorem (see [Reference Brauer and Nesbitt3], and for our application, see [Reference Eggermont9, Theorem 5.7]) that
$\overline {\rho }_{E,p}$
is irreducible, it follows from Brauer–Nesbitt theorem (see [Reference Brauer and Nesbitt3], and for our application, see [Reference Eggermont9, Theorem 5.7]) that
![]() $\overline {\rho }_{E,p}$
and
$\overline {\rho }_{E,p}$
and
![]() $ \overline {\rho }_{E',p}$
are isomorphic.
$ \overline {\rho }_{E',p}$
are isomorphic.
To complete the proof, we must eliminate the possibility that
![]() $\overline {\rho }_{E,p}$
and
$\overline {\rho }_{E,p}$
and
![]() $ \overline {\rho }_{E',p}$
are isomorphic. Recall that, by Corollary 3.10, the mod p Galois representation
$ \overline {\rho }_{E',p}$
are isomorphic. Recall that, by Corollary 3.10, the mod p Galois representation
![]() $\overline {\rho }_{E,p}$
is absolutely irreducible, but
$\overline {\rho }_{E,p}$
is absolutely irreducible, but
![]() $\overline {\rho }_{E',p}$
can never be absolutely irreducible since
$\overline {\rho }_{E',p}$
can never be absolutely irreducible since
![]() $E'$
has CM. This proves Case II of Theorem 1.2.
$E'$
has CM. This proves Case II of Theorem 1.2.
Remark 5.2 For simplicity, we only considered the fields where there is only one prime ideal lying above
![]() $3$
, so we excluded the fields
$3$
, so we excluded the fields
![]() ${\mathbb Q}(\sqrt {-2})$
and
${\mathbb Q}(\sqrt {-2})$
and
![]() ${\mathbb Q}(\sqrt {-11})$
. Note that the triple
${\mathbb Q}(\sqrt {-11})$
. Note that the triple
![]() $(\omega ,\omega ^2,1)$
, where
$(\omega ,\omega ^2,1)$
, where
![]() $\omega $
is a primitive third root of unity, is a solution to equation (1.1). Hence, we had to exclude the case
$\omega $
is a primitive third root of unity, is a solution to equation (1.1). Hence, we had to exclude the case
![]() ${\mathbb Q}(\sqrt {-3})$
.
${\mathbb Q}(\sqrt {-3})$
.
One can try to apply the argument above to deal with the Fermat equation with signature
![]() $(p,p,3)$
defined over the imaginary quadratic field
$(p,p,3)$
defined over the imaginary quadratic field
![]() ${\mathbb Q}(\sqrt {-163})$
. However, we were unable to compute all the Bianchi modular forms over
${\mathbb Q}(\sqrt {-163})$
. However, we were unable to compute all the Bianchi modular forms over
![]() ${\mathbb Q}(\sqrt {-163})$
at level
${\mathbb Q}(\sqrt {-163})$
at level
![]() $\lambda ^3$
.
$\lambda ^3$
.
A Appendix. Ternary equation of signature
 $(p,p,2)$
$(p,p,2)$
In [Reference Işik, Kara and Ozman14], we have proved that the equation
![]() $x^p+y^p=z^2$
has no solutions asymptotically where
$x^p+y^p=z^2$
has no solutions asymptotically where
![]() $2|b$
over certain number fields. Using the method in the proof of Theorem 1.1, we can extend the results to any number field K with
$2|b$
over certain number fields. Using the method in the proof of Theorem 1.1, we can extend the results to any number field K with
![]() $h_K^+=1$
. The difference relies in the proof method. Generally speaking, in order to solve a Diophantine equation using the modular method, one needs to either compute newforms of a certain level or compute all elliptic curves of a given conductor and particular information about torsion subgroup and/or rational isogeny or compute all solutions to an S-unit equation.
$h_K^+=1$
. The difference relies in the proof method. Generally speaking, in order to solve a Diophantine equation using the modular method, one needs to either compute newforms of a certain level or compute all elliptic curves of a given conductor and particular information about torsion subgroup and/or rational isogeny or compute all solutions to an S-unit equation.
In [Reference Işik, Kara and Ozman14], we used the S-unit equation method and this restricted us to the totally real number fields. However, using Theorem 4.1 as we did for proving Theorem 1.1, we can get the following result about the solutions of
![]() $x^p+y^p=z^2$
.
$x^p+y^p=z^2$
.
Theorem A.1 Let K be a number field with narrow class number
![]() $h_K^{+}=1$
satisfying Conjectures 2.2 and 2.3. Assume that
$h_K^{+}=1$
satisfying Conjectures 2.2 and 2.3. Assume that
![]() $\beta $
is the only prime of K lying above
$\beta $
is the only prime of K lying above
![]() $2$
. Let
$2$
. Let
![]() $W_K$
be the set of
$W_K$
be the set of
![]() $(a,b,c)\in {\mathcal O}_K$
such that
$(a,b,c)\in {\mathcal O}_K$
such that
![]() $a^p+b^p=c^2$
with
$a^p+b^p=c^2$
with
![]() $\beta |b$
. Then there is a constant
$\beta |b$
. Then there is a constant
![]() $B_K$
—depending only on K—such that, for
$B_K$
—depending only on K—such that, for
![]() $p> B_K$
, the equation
$p> B_K$
, the equation
![]() $x^p+y^P=z^2$
has no solution
$x^p+y^P=z^2$
has no solution
![]() $(a,b,c) \in W_K$
.
$(a,b,c) \in W_K$
.
A hypothetical solution
![]() $(a,b,c) \in W_K$
with exponent
$(a,b,c) \in W_K$
with exponent
![]() $p>B_K$
gives rise to an elliptic curve
$p>B_K$
gives rise to an elliptic curve
![]() $E'/K$
with a K-rational
$E'/K$
with a K-rational
![]() $2$
-isogeny, good reduction away from
$2$
-isogeny, good reduction away from
![]() ${\mathfrak P}$
and potentially multiplicative reduction at
${\mathfrak P}$
and potentially multiplicative reduction at
![]() ${\mathfrak P}$
. However, this contradicts with Theorem 4.1, and hence there is no such a solution.
${\mathfrak P}$
. However, this contradicts with Theorem 4.1, and hence there is no such a solution.
Now, we give some examples of totally real number fields with
![]() $h_K^{+}=1$
, in which
$h_K^{+}=1$
, in which
![]() $2$
is totally ramified.
$2$
is totally ramified.
Degree
![]() $2^n$
case. Let
$2^n$
case. Let
![]() $f_1(x)=x^2-2$
, and
$f_1(x)=x^2-2$
, and
![]() $f_n(x)= (f_{n-1}(x))^2-2$
for
$f_n(x)= (f_{n-1}(x))^2-2$
for
![]() $n \geq 2$
. Let
$n \geq 2$
. Let
![]() $K_n={\mathbb Q}(\theta _n)$
, where
$K_n={\mathbb Q}(\theta _n)$
, where
![]() $\theta _n $
is a root of the polynomial
$\theta _n $
is a root of the polynomial
![]() $f_n(x)$
. Then it can be seen that
$f_n(x)$
. Then it can be seen that
![]() $K_n={\mathbb Q}(\sqrt {2+ \cdots +\sqrt {2}}) = {\mathbb Q}(\zeta _{2^{n+2}}+\zeta _{2^{n+2}}^{-1})$
, the maximal totally real subfield of
$K_n={\mathbb Q}(\sqrt {2+ \cdots +\sqrt {2}}) = {\mathbb Q}(\zeta _{2^{n+2}}+\zeta _{2^{n+2}}^{-1})$
, the maximal totally real subfield of
![]() ${\mathbb Q}(\zeta _{2^{n+2}})$
. Then,
${\mathbb Q}(\zeta _{2^{n+2}})$
. Then,
![]() $K_n$
is a totally real number field of degree
$K_n$
is a totally real number field of degree
![]() $2^n$
in which
$2^n$
in which
![]() $2$
is totally ramified. For
$2$
is totally ramified. For
![]() $2 \leq n \leq 5$
, it is possible to check that the narrow class number of
$2 \leq n \leq 5$
, it is possible to check that the narrow class number of
![]() $K_n$
is
$K_n$
is
![]() $1$
, and hence it follows from Corollary 6.5 of [Reference Işik, Kara and Ozman14] that the asymptotic FLT holds for all
$1$
, and hence it follows from Corollary 6.5 of [Reference Işik, Kara and Ozman14] that the asymptotic FLT holds for all
![]() $K_n$
with
$K_n$
with
![]() $ 2 \leq n \leq 5$
. For some other higher values of n, it is only conjecturally true that the narrow class number is
$ 2 \leq n \leq 5$
. For some other higher values of n, it is only conjecturally true that the narrow class number is
![]() $1$
(using MAGMA under GRH).
$1$
(using MAGMA under GRH).
Degree
![]() $3,4,5$
case. For
$3,4,5$
case. For
![]() $n \geq 3$
, let
$n \geq 3$
, let
![]() $\mathcal {F}_n$
be the set of totally real number fields of degree n, discriminant
$\mathcal {F}_n$
be the set of totally real number fields of degree n, discriminant
![]() $\leq 10^6$
, in which
$\leq 10^6$
, in which
![]() $2$
totally ramifies. We are able to find the complete sets
$2$
totally ramifies. We are able to find the complete sets
![]() $\mathcal {F}_3, \mathcal {F}_4$
, and
$\mathcal {F}_3, \mathcal {F}_4$
, and
![]() $\mathcal {F}_5$
in the John Jones Number Field Database [Reference Jones and Roberts15]. We define the following sets:
$\mathcal {F}_5$
in the John Jones Number Field Database [Reference Jones and Roberts15]. We define the following sets:
-
• Let
 $\mathcal {G}_n$
be the set of
$\mathcal {G}_n$
be the set of
 $K \in \mathcal {F}_n$
such that
$K \in \mathcal {F}_n$
such that
 $h_K^+$
is odd.
$h_K^+$
is odd. -
• Let
 $\mathcal {K}_n$
be the set of
$\mathcal {K}_n$
be the set of
 $K \in \mathcal {G}_n$
such that
$K \in \mathcal {G}_n$
such that
 $h_K^+=1$
.
$h_K^+=1$
.
Of course,
![]() $ \mathcal {K}_n \subseteq \mathcal {G}_n \subseteq \mathcal {F}_n$
, and the asymptotic FLT holds for any K belonging to
$ \mathcal {K}_n \subseteq \mathcal {G}_n \subseteq \mathcal {F}_n$
, and the asymptotic FLT holds for any K belonging to
![]() $\mathcal {K}_n$
by Corollary 6.5 of [Reference Işik, Kara and Ozman14]. The cardinalities of
$\mathcal {K}_n$
by Corollary 6.5 of [Reference Işik, Kara and Ozman14]. The cardinalities of
![]() $ \mathcal {K}_n , \mathcal {G}_n ,$
and
$ \mathcal {K}_n , \mathcal {G}_n ,$
and
![]() $ \mathcal {F}_n$
are given in the following table, and can be found online at https://sites.google.com/view/erman-isik/research?authuser=0.
$ \mathcal {F}_n$
are given in the following table, and can be found online at https://sites.google.com/view/erman-isik/research?authuser=0.

Acknowledgment
We are grateful to Samir Siksek for very helpful comments and discussions. We also would like to thank the referees for their comments and corrections which improved the paper a lot.