We prove the existence of positive solutions to a semipositone p-Laplacian problem combining mountain pass arguments, comparison principles, regularity principles and a priori estimates.

We study the existence of non-trivial solutions for a class of asymptotically periodic semilinear Schrödinger equations in ℝN. By combining variational methods and the concentration-compactness principle, we obtain a non-trivial solution for the asymptotically periodic case and a ground state solution for the periodic one. In the proofs we apply the mountain pass theorem and its local version.

We provide an existence result of radially symmetric, positive, classical solutions for a nonlinear Schrödinger equation driven by the infinitesimal generator of a rotationally invariant Lévy process.

We consider a nonlinear periodic problem driven by the scalar p-Laplacian and with a reaction term which exhibits a (p – 1)-superlinear growth near ±∞ but need not satisfy the Ambrosetti-Rabinowitz condition. Combining critical point theory with Morse theory we prove an existence theorem. Then, using variational methods together with truncation techniques, we prove a multiplicity theorem establishing the existence of at least five non-trivial solutions, with precise sign information for all of them (two positive solutions, two negative solutions and a nodal (sign changing) solution).

We consider a nonlinear periodic problem driven by a nonlinear nonhomogeneous differential operator and a Carathéodory reaction term $f\left( t,\,x \right)$ that exhibits a $\left( p\,-\,1 \right)$-superlinear growth in $x\,\in \,\mathbb{R}$ near $\pm \infty $ and near zero. A special case of the differential operator is the scalar $p$-Laplacian. Using a combination of variational methods based on the critical point theory with Morse theory (critical groups), we show that the problem has three nontrivial solutions, two of which have constant sign (one positive, the other negative).

In this paper we study impulsive periodic solutions for second-order nonautonomous singular differential equations. Our proof is based on the mountain pass theorem. Some recent results in the literature are extended.

We prove the existence of a positive solution to the BVP $$(\Phi(t)u'(t))'=f(t,u(t)),\,\,\,\,\,\,\,\,\,\,\,u'(0)=u(1)=0, $$ 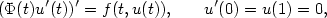imposing some conditions on Φ and f. In particular, weassume $\Phi(t)f(t,u)$ 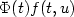to be decreasing in t. Our methodcombines variational and topological arguments and can be appliedto some elliptic problems in annular domains. An $L_\infty$ 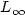boundfor the solution is provided by the $L_\infty$ 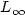norm of any testfunction with negative energy.

A second-order Hamiltonian system with time recurrence is studied. The recurrence condition is weaker than almost periodicity. The existence is proven of an infinite family of solutions homoclinic to zerowhose support is spread out overthe real line.

In this paper we complete two tasks. First we extend the nonsmooth critical point theory of Chang to the case where the energy functional satisfies only the weaker nonsmooth Cerami condition and we also relax the boundary conditions. Then we study semilinear and quasilinear equations (involving the p-Laplacian). Using a variational approach we establish the existence of one and of multiple solutions. In simple existence theorems, we allow the right hand side to be discontinuous. In that case in order to have an existence theory, we pass to a multivalued approximation of the original problem by, roughly speaking, filling in the gaps at the discontinuity points.