1 results
Limiting empirical spectral distribution for the non-backtracking matrix of an Erdős-Rényi random graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 31 July 2023, pp. 956-973
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
In this note, we give a precise description of the limiting empirical spectral distribution for the non-backtracking matrices for an Erdős-Rényi graph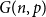
$G(n,p)$ assuming 
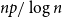$np/\log n$ tends to infinity. We show that derandomizing part of the non-backtracking random matrix simplifies the spectrum considerably, and then, we use Tao and Vu’s replacement principle and the Bauer-Fike theorem to show that the partly derandomized spectrum is, in fact, very close to the original spectrum.
