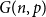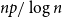1. Introduction
For a simple undirected graph
![]() $G=(V,E)$
, the non-backtracking matrix is defined as follows. For each
$G=(V,E)$
, the non-backtracking matrix is defined as follows. For each
![]() $(i,j) \in E$
, form two directed edges
$(i,j) \in E$
, form two directed edges
![]() $i \to j$
and
$i \to j$
and
![]() $j \to i$
. The non-backtracking matrix
$j \to i$
. The non-backtracking matrix
![]() $B$
is a
$B$
is a
![]() $2|E| \times 2|E|$
matrix such that
$2|E| \times 2|E|$
matrix such that
 \begin{equation*}B_{i\to j, k\to l}= \begin {cases} 1 & \text {if}\ j=k \, \text {and}\ i\neq l \\[5pt] 0 & \text {otherwise}. \end {cases} \end{equation*}
\begin{equation*}B_{i\to j, k\to l}= \begin {cases} 1 & \text {if}\ j=k \, \text {and}\ i\neq l \\[5pt] 0 & \text {otherwise}. \end {cases} \end{equation*}
The central question of the current paper is the following:
Question 1.1.
What can be said about the eigenvalues of the non-backtracking matrix
![]() $B$
of random graphs as
$B$
of random graphs as
![]() $|V|\to \infty$
?
$|V|\to \infty$
?
The non-backtracking matrix was proposed by Hashimoto [Reference Hashimoto17]. The spectrum of the non-backtracking matrix for random graphs was studied by Angel, Friedman, and Hoory [Reference Angel, Friedman and Hoory2] in the case where the underlying graph is the tree covering of a finite graph. Motivated by the question of community detection (see [Reference Krzakala, Moore and Mossel23, Reference Massoulié29–Reference Mossel, Neeman and Sly31]), Bordenave, Lelarge, and Massoulié [Reference Bordenave, Lelarge and Massoulié8] determined the size of the largest eigenvalue and gave bounds for the sizes of all other eigenvalues for non-backtracking matrices when the underlying graph is drawn from a generalization of Erdős-Rényi random graphs called the Stochastic Block Model (see [Reference Holland, Laskey and Leinhardt19]), and this work was further extended to the Degree-Corrected Stochastic Block Model (see [Reference Karrer and Newman24]) by Gulikers, Lelarge, and Massoulié [Reference Gulikers, Lelarge and Massoulié15]. In recent work, Benaych-Georges, Bordenave, and Knowles [Reference Benaych-Georges, Bordenave and Knowles5] studied the spectral radii of the sparse inhomogeneous Erdős-Rényi graph through a novel application of non-backtracking matrices. Stephan and Massoulié [Reference Stephan and Massoulié32] also conducted a study on the non-backtracking spectra of weighted inhomogeneous random graphs.
In the current paper, we give a precise characterization of the limiting distribution of the eigenvalues for the non-backtracking matrix when the underlying graph is the Erdős-Rényi random graph
![]() $G(n,p)$
, where each edge
$G(n,p)$
, where each edge
![]() $ij$
is present independently with probability
$ij$
is present independently with probability
![]() $p$
, and where we exclude loops (edges of the form
$p$
, and where we exclude loops (edges of the form
![]() $ii$
). We will allow
$ii$
). We will allow
![]() $p$
to be constant or decreasing sublinearly with
$p$
to be constant or decreasing sublinearly with
![]() $n$
, which contrasts to the bounds proved in [Reference Bordenave, Lelarge and Massoulié8] and [Reference Gulikers, Lelarge and Massoulié15] corresponding to the case
$n$
, which contrasts to the bounds proved in [Reference Bordenave, Lelarge and Massoulié8] and [Reference Gulikers, Lelarge and Massoulié15] corresponding to the case
![]() $p=c/n$
with
$p=c/n$
with
![]() $c$
a constant. Let
$c$
a constant. Let
![]() $A$
be the adjacency matrix of
$A$
be the adjacency matrix of
![]() $G(n,p)$
, so
$G(n,p)$
, so
![]() $A_{ij}=1$
exactly when edge
$A_{ij}=1$
exactly when edge
![]() $ij$
is part of the graph
$ij$
is part of the graph
![]() $G$
and
$G$
and
![]() $A_{ij}=0$
otherwise, and let
$A_{ij}=0$
otherwise, and let
![]() $D$
the diagonal matrix with
$D$
the diagonal matrix with
![]() $D_{ii}=\sum _{j=1}^n A_{ij}$
. Much is known about the eigenvalues of
$D_{ii}=\sum _{j=1}^n A_{ij}$
. Much is known about the eigenvalues of
![]() $A$
, going back to works of Wigner in the 1950s [Reference Wigner38, Reference Wigner39] (see also [Reference Grenander16] and [Reference Arnold3]), who proved that the distribution of eigenvalues follows the semicircular law for any constant
$A$
, going back to works of Wigner in the 1950s [Reference Wigner38, Reference Wigner39] (see also [Reference Grenander16] and [Reference Arnold3]), who proved that the distribution of eigenvalues follows the semicircular law for any constant
![]() $p\in (0,1)$
. More recent results have considered the case where
$p\in (0,1)$
. More recent results have considered the case where
![]() $p$
tends to zero, making the random graph sparse. It is known that assuming
$p$
tends to zero, making the random graph sparse. It is known that assuming
![]() $np\to \infty$
, the empirical spectral distribution (ESD) of the adjacency matrix
$np\to \infty$
, the empirical spectral distribution (ESD) of the adjacency matrix
![]() $A$
converges to the semicircle distribution (see for example [Reference Khorunzhy and Pastur25] or [Reference Tran, Van and Wang35]). Actually, much stronger results have been proved about the eigenvalues of
$A$
converges to the semicircle distribution (see for example [Reference Khorunzhy and Pastur25] or [Reference Tran, Van and Wang35]). Actually, much stronger results have been proved about the eigenvalues of
![]() $A$
(see the surveys [Reference Vu37] and [Reference Benaych-Georges and Knowles6]). For example, Erdős, Knowles, Yau, and Yin [Reference Erdős, Knowles, Yau and Yin12] proved that as long as there is a constant
$A$
(see the surveys [Reference Vu37] and [Reference Benaych-Georges and Knowles6]). For example, Erdős, Knowles, Yau, and Yin [Reference Erdős, Knowles, Yau and Yin12] proved that as long as there is a constant
![]() $C$
so that
$C$
so that
![]() $np > (\log n)^{C \log \log n}$
(and thus
$np > (\log n)^{C \log \log n}$
(and thus
![]() $np\to \infty$
faster than logarithmic speed), the eigenvalues of the adjacency matrix
$np\to \infty$
faster than logarithmic speed), the eigenvalues of the adjacency matrix
![]() $A$
satisfy a result called the local semicircle law. This law characterizes the distribution of the eigenvalues in small intervals that shrink as the size of the matrix
$A$
satisfy a result called the local semicircle law. This law characterizes the distribution of the eigenvalues in small intervals that shrink as the size of the matrix
![]() $n$
increases. The most recent development regarding the local semicircle law can be found in [Reference He, Knowles and Marcozzi14] and [Reference Alt, Ducatez and Knowles1].
$n$
increases. The most recent development regarding the local semicircle law can be found in [Reference He, Knowles and Marcozzi14] and [Reference Alt, Ducatez and Knowles1].
It has been shown in [Reference Angel, Friedman and Hoory2, Reference Bass4, Reference Hashimoto17] (for example, Theorem 1.5 from [Reference Angel, Friedman and Hoory2]) that the spectrum of
![]() $B$
is the set
$B$
is the set
![]() $\{ \pm 1\} \cup \{\mu : \det (\mu ^2 I - \mu A + D-I) =0\}$
, or equivalently, the set
$\{ \pm 1\} \cup \{\mu : \det (\mu ^2 I - \mu A + D-I) =0\}$
, or equivalently, the set
![]() $\{ \pm 1\} \cup \{\text{eigenvalues of } H \},$
where
$\{ \pm 1\} \cup \{\text{eigenvalues of } H \},$
where
 \begin{equation} H = \begin{pmatrix} A & I-D\\[5pt] I & 0 \end{pmatrix}. \end{equation}
\begin{equation} H = \begin{pmatrix} A & I-D\\[5pt] I & 0 \end{pmatrix}. \end{equation}
We will call this
![]() $2n \times 2n$
matrix
$2n \times 2n$
matrix
![]() $H$
the non-backtracking spectrum operator for
$H$
the non-backtracking spectrum operator for
![]() $A$
, and we will show that the spectrum of
$A$
, and we will show that the spectrum of
![]() $H$
may be precisely described, thus giving a precise description of the eigenvalues of the non-backtracking matrix
$H$
may be precisely described, thus giving a precise description of the eigenvalues of the non-backtracking matrix
![]() $B$
. We will study the eigenvalues of
$B$
. We will study the eigenvalues of
![]() $H$
in two regions: the dense region, where
$H$
in two regions: the dense region, where
![]() $p \in (0,1)$
and
$p \in (0,1)$
and
![]() $p$
is fixed constant; and the sparse region, where
$p$
is fixed constant; and the sparse region, where
![]() $p=o(1)$
and
$p=o(1)$
and
![]() $np \to \infty$
. The diluted region, where
$np \to \infty$
. The diluted region, where
![]() $p=c/n$
for some constant
$p=c/n$
for some constant
![]() $c>1$
, is the region for which the bounds in [Reference Bordenave, Lelarge and Massoulié8] and [Reference Gulikers, Lelarge and Massoulié15] apply, and, as pointed out by [Reference Bordenave, Lelarge and Massoulié8], it would be interesting to determine the limiting eigenvalue distribution of
$c>1$
, is the region for which the bounds in [Reference Bordenave, Lelarge and Massoulié8] and [Reference Gulikers, Lelarge and Massoulié15] apply, and, as pointed out by [Reference Bordenave, Lelarge and Massoulié8], it would be interesting to determine the limiting eigenvalue distribution of
![]() $H$
in this region.
$H$
in this region.
Note that
![]() ${\mathbb E }(D) = (n-1)p I$
, and so we will let
${\mathbb E }(D) = (n-1)p I$
, and so we will let
and consider the partly averaged matrix
 \begin{equation} H_0= \begin{pmatrix} A & I-{\mathbb E }(D)\\[5pt] I & 0 \end{pmatrix} = \begin{pmatrix} A & -\alpha I\\[5pt] I & 0 \end{pmatrix}. \end{equation}
\begin{equation} H_0= \begin{pmatrix} A & I-{\mathbb E }(D)\\[5pt] I & 0 \end{pmatrix} = \begin{pmatrix} A & -\alpha I\\[5pt] I & 0 \end{pmatrix}. \end{equation}
The partly averaged matrix
![]() $H_0$
will be an essential tool in quantifying the eigenvalues of the non-backtracking spectrum operator
$H_0$
will be an essential tool in quantifying the eigenvalues of the non-backtracking spectrum operator
![]() $H$
. Three main ideas are at the core of this paper: first, that partial derandomization can greatly simplify the spectrum; second, that Tao and Vu’s replacement principle [Reference Tao and Van34, Theorem 2.1] can be usefully applied to two sequences of random matrices that are highly dependent on each other; and third, that in this case, the partly derandomized matrix may be viewed as a small perturbation of the original matrix, allowing one to apply results from perturbation theory like the Bauer-Fike Theorem. The use of Tao and Vu’s replacement principle here is novel, as it is used to compare the spectra of a sequence of matrices with some dependencies among the entries to a sequence of matrices where all random entries are independent; typically, the Tao-Vu replacement principle has been applied in cases where the two sequences of random matrices both have independent entries, see for example [Reference Tao and Van34, Reference Wood40, Reference Wood41].
$H$
. Three main ideas are at the core of this paper: first, that partial derandomization can greatly simplify the spectrum; second, that Tao and Vu’s replacement principle [Reference Tao and Van34, Theorem 2.1] can be usefully applied to two sequences of random matrices that are highly dependent on each other; and third, that in this case, the partly derandomized matrix may be viewed as a small perturbation of the original matrix, allowing one to apply results from perturbation theory like the Bauer-Fike Theorem. The use of Tao and Vu’s replacement principle here is novel, as it is used to compare the spectra of a sequence of matrices with some dependencies among the entries to a sequence of matrices where all random entries are independent; typically, the Tao-Vu replacement principle has been applied in cases where the two sequences of random matrices both have independent entries, see for example [Reference Tao and Van34, Reference Wood40, Reference Wood41].
1.1 Results
Throughout the rest of this paper, we mainly focus on sparse random graphs where
![]() $p\in (0,1)$
may tend to zero as
$p\in (0,1)$
may tend to zero as
![]() $n\to \infty$
. Our first result shows that the spectrum of
$n\to \infty$
. Our first result shows that the spectrum of
![]() $H_0$
can be determined very precisely in terms of the spectrum of the random Hermitian matrix
$H_0$
can be determined very precisely in terms of the spectrum of the random Hermitian matrix
![]() $A$
, which is well-understood.
$A$
, which is well-understood.
Proposition 1.2 (Spectrum of the partly averaged matrix). Let
![]() $H_0$
be defined as in (1.2), and let
$H_0$
be defined as in (1.2), and let
![]() $0< p\le p_0<1$
for a constant
$0< p\le p_0<1$
for a constant
![]() $p_0$
. If
$p_0$
. If
![]() $p\ge C/\sqrt{n}$
for some large constant
$p\ge C/\sqrt{n}$
for some large constant
![]() $C>0$
, then, with probability
$C>0$
, then, with probability
![]() $1-o(1)$
,
$1-o(1)$
,
![]() $\frac{1}{\sqrt{\alpha }} H_0$
has two real eigenvalues
$\frac{1}{\sqrt{\alpha }} H_0$
has two real eigenvalues
![]() $\mu _1$
and
$\mu _1$
and
![]() $\mu _2$
satisfying
$\mu _2$
satisfying
![]() $\mu _1=\sqrt{\alpha } (1+o(1))$
and
$\mu _1=\sqrt{\alpha } (1+o(1))$
and
![]() $\mu _2 = 1/\sqrt{np} (1+o(1))$
; all other eigenvalues for
$\mu _2 = 1/\sqrt{np} (1+o(1))$
; all other eigenvalues for
![]() $\frac{1}{\sqrt{\alpha }} H_0$
are complex with magnitude
$\frac{1}{\sqrt{\alpha }} H_0$
are complex with magnitude
![]() $1$
and occur in complex conjugate pairs. If
$1$
and occur in complex conjugate pairs. If
![]() $np \to \infty$
with
$np \to \infty$
with
![]() $n$
, then the real parts of the eigenvalues in the circular arcs are distributed according to the semicircle law.
$n$
, then the real parts of the eigenvalues in the circular arcs are distributed according to the semicircle law.
Remark 1.3. When
![]() $n^{-1+\epsilon }\le p\le n^{-1/2}$
, more real eigenvalues of
$n^{-1+\epsilon }\le p\le n^{-1/2}$
, more real eigenvalues of
![]() $H_0$
will emerge. We provide a short discussion on the real eigenvalues of
$H_0$
will emerge. We provide a short discussion on the real eigenvalues of
![]() $H_0$
in Section 2.2. Note that as long as the number of real eigenvalues is bounded by a fixed constant, for example when
$H_0$
in Section 2.2. Note that as long as the number of real eigenvalues is bounded by a fixed constant, for example when
![]() $p \ge C/\sqrt n$
, the bulk distribution of
$p \ge C/\sqrt n$
, the bulk distribution of
![]() $H_0$
is two arcs on the unit circle, with density so that real parts of the eigenvalues follow the semicircular law.
$H_0$
is two arcs on the unit circle, with density so that real parts of the eigenvalues follow the semicircular law.
The spectrum of the non-backtracking matrix for a degree regular graph was studied in [Reference Bordenave7], including proving some precise eigenvalue estimates. One can view Proposition 1.2 as extending this general approach by using averaged degree counts, but allowing the graph to no longer be degree regular. Thus, Proposition 1.2 shows that partly averaging
![]() $H$
to get
$H$
to get
![]() $H_0$
is enough to allow the spectrum to be computed very precisely. Our main results are the theorems below, which show that the empirical spectral measures
$H_0$
is enough to allow the spectrum to be computed very precisely. Our main results are the theorems below, which show that the empirical spectral measures
![]() $\mu _H$
for
$\mu _H$
for
![]() $H$
and
$H$
and
![]() $\mu _{H_0}$
for
$\mu _{H_0}$
for
![]() $H_0$
are very close to each other, even for
$H_0$
are very close to each other, even for
![]() $p$
a decreasing function of
$p$
a decreasing function of
![]() $n$
. (The definitions of the measure
$n$
. (The definitions of the measure
![]() $\mu _M$
for a matrix
$\mu _M$
for a matrix
![]() $M$
and the definition of almost sure convergence of measures are given in Section 1.3).
$M$
and the definition of almost sure convergence of measures are given in Section 1.3).
Theorem 1.4.
Let
![]() $A$
be the adjacency matrix for an Erdős-Rényi random graph
$A$
be the adjacency matrix for an Erdős-Rényi random graph
![]() $G(n,p)$
. Assume
$G(n,p)$
. Assume
![]() $0< p\le p_0<1$
for a constant
$0< p\le p_0<1$
for a constant
![]() $p_0$
and
$p_0$
and
![]() $np/\log n \to \infty$
with
$np/\log n \to \infty$
with
![]() $n$
. Let
$n$
. Let
![]() $\frac{1}{\sqrt{\alpha }} H$
be a rescaling of the non-backtracking spectrum operator for
$\frac{1}{\sqrt{\alpha }} H$
be a rescaling of the non-backtracking spectrum operator for
![]() $A$
defined in (
1.1
) with
$A$
defined in (
1.1
) with
![]() $\alpha = (n-1)p-1$
, and let
$\alpha = (n-1)p-1$
, and let
![]() $\frac{1}{\sqrt{\alpha }} H_0$
be its partial derandomization, defined in (
1.2
). Then,
$\frac{1}{\sqrt{\alpha }} H_0$
be its partial derandomization, defined in (
1.2
). Then,
![]() $\mu _{\frac{1}{\sqrt{\alpha }}H} - \mu _{\frac{1}{\sqrt{\alpha }} H_0}$
converges almost surely (thus, also in probability) to zero as
$\mu _{\frac{1}{\sqrt{\alpha }}H} - \mu _{\frac{1}{\sqrt{\alpha }} H_0}$
converges almost surely (thus, also in probability) to zero as
![]() $n$
goes to infinity.
$n$
goes to infinity.
Remark 1.5. When
![]() $p\gg \log n/n$
, the graph
$p\gg \log n/n$
, the graph
![]() $G(n,p)$
is almost a random regular graph and thus
$G(n,p)$
is almost a random regular graph and thus
![]() $H_0$
appears to be a good approximation of
$H_0$
appears to be a good approximation of
![]() $H$
. When
$H$
. When
![]() $p$
becomes smaller, such an approximation is no longer accurate. In this sense, Theorem 1.4 is optimal.
$p$
becomes smaller, such an approximation is no longer accurate. In this sense, Theorem 1.4 is optimal.
In Figure 1, we plot the eigenvalues of
![]() $\frac{1}{\sqrt{\alpha }}H$
and
$\frac{1}{\sqrt{\alpha }}H$
and
![]() $\frac{1}{\sqrt{\alpha }}H_0$
for an Erdős-Rényi random graph
$\frac{1}{\sqrt{\alpha }}H_0$
for an Erdős-Rényi random graph
![]() $G(n,p)$
, where
$G(n,p)$
, where
![]() $n=500$
. The blue circles mark the eigenvalues for
$n=500$
. The blue circles mark the eigenvalues for
![]() $H/\sqrt{\alpha }$
and the red x’s mark the eigenvalues for
$H/\sqrt{\alpha }$
and the red x’s mark the eigenvalues for
![]() $H_0/\sqrt{\alpha }$
. We can see that the empirical spectral measures of
$H_0/\sqrt{\alpha }$
. We can see that the empirical spectral measures of
![]() $H/\sqrt{\alpha }$
and
$H/\sqrt{\alpha }$
and
![]() $H_0/\sqrt{\alpha }$
are very close for
$H_0/\sqrt{\alpha }$
are very close for
![]() $p$
not too small. As
$p$
not too small. As
![]() $p$
becomes smaller (note that here
$p$
becomes smaller (note that here
![]() $\log n/n\approx 0.0054$
), the eigenvalues of
$\log n/n\approx 0.0054$
), the eigenvalues of
![]() $H_0/\sqrt{\alpha }$
still lie on the arcs of the unit circle whereas the eigenvalues of
$H_0/\sqrt{\alpha }$
still lie on the arcs of the unit circle whereas the eigenvalues of
![]() $H/\sqrt{\alpha }$
start to escape and be attracted to the inside of the circle.
$H/\sqrt{\alpha }$
start to escape and be attracted to the inside of the circle.

Figure 1. The eigenvalues of
![]() $H/\sqrt{\alpha }$
defined in (1.1) and
$H/\sqrt{\alpha }$
defined in (1.1) and
![]() $H_0/\sqrt{\alpha }$
defined in (1.2) for a sample of
$H_0/\sqrt{\alpha }$
defined in (1.2) for a sample of
![]() $G(n,p)$
with
$G(n,p)$
with
![]() $n=500$
and different values of
$n=500$
and different values of
![]() $p$
. The blue circles are the eigenvalues of
$p$
. The blue circles are the eigenvalues of
![]() $H/\sqrt{\alpha }$
, and the red x’s are for
$H/\sqrt{\alpha }$
, and the red x’s are for
![]() $H_0/\sqrt{\alpha }$
. For comparison, the black dashed line is the unit circle. For the figures from top to bottom and from left to right, the values of
$H_0/\sqrt{\alpha }$
. For comparison, the black dashed line is the unit circle. For the figures from top to bottom and from left to right, the values of
![]() $p$
are taken to be
$p$
are taken to be
![]() $p=0.5, p=0.1, p=0.08$
and
$p=0.5, p=0.1, p=0.08$
and
![]() $p=0.05$
, respectively.
$p=0.05$
, respectively.
To prove that the bulk eigenvalue distributions converge in Theorem 1.4, we will use Tao and Vu’s replacement principle [Reference Tao and Van34, Theorem 2.1] (see also Theorem 3.2), which was a key step in proving the circular law. The replacement principle lets one compare eigenvalue distributions of two sequences of random matrices, and it has often been used in cases where one type of random input – for example, standard Gaussian normal entries – is replaced by a different type of random input – for example, arbitrary mean 0, variance 1 entries. This is how the replacement principle was used to prove the circular law in [Reference Tao and Van34], and it was used similarly in, for example, [Reference Wood40, Reference Wood41]. The application of the replacement principle in the current paper is distinct in that the entries for one ensemble of random matrices, namely
![]() $H$
, has some dependencies between the entries, whereas the random entries of
$H$
, has some dependencies between the entries, whereas the random entries of
![]() $H_0$
are all independent.
$H_0$
are all independent.
Our third result (Theorem 1.6 below) proves that all eigenvalues of
![]() $H$
are close to those of
$H$
are close to those of
![]() $H_0$
with high probability when
$H_0$
with high probability when
![]() $p\gg \frac{\log ^{2/3} n}{n^{1/6}}$
, which implies that there are no outlier eigenvalues of
$p\gg \frac{\log ^{2/3} n}{n^{1/6}}$
, which implies that there are no outlier eigenvalues of
![]() $H$
, that is, no eigenvalues of
$H$
, that is, no eigenvalues of
![]() $H$
that are far outside the support of the spectrum of
$H$
that are far outside the support of the spectrum of
![]() $H_0$
(described in Theorem 1.2).
$H_0$
(described in Theorem 1.2).
Theorem 1.6.
Assume
![]() $0<p\le p_0<1$
for a constant
$0<p\le p_0<1$
for a constant
![]() $p_0$
and
$p_0$
and
![]() $p\ge \frac{\log ^{2/3+\varepsilon } n}{n^{1/6}}$
for
$p\ge \frac{\log ^{2/3+\varepsilon } n}{n^{1/6}}$
for
![]() $\varepsilon >0$
. Let
$\varepsilon >0$
. Let
![]() $A$
be the adjacency matrix for an Erdős-Rényi random graph
$A$
be the adjacency matrix for an Erdős-Rényi random graph
![]() $G(n,p)$
. Let
$G(n,p)$
. Let
![]() $\frac{1}{\sqrt{\alpha }} H$
be a rescaling of the non-backtracking spectrum operator for
$\frac{1}{\sqrt{\alpha }} H$
be a rescaling of the non-backtracking spectrum operator for
![]() $A$
defined in (
1.1
). Then, with probability
$A$
defined in (
1.1
). Then, with probability
![]() $1-o(1)$
, each eigenvalue of
$1-o(1)$
, each eigenvalue of
![]() $\frac{1}{\sqrt{\alpha }} H$
is within distance
$\frac{1}{\sqrt{\alpha }} H$
is within distance
![]() $R= 40\sqrt{\frac{\log n}{np^2}}$
of an eigenvalue of
$R= 40\sqrt{\frac{\log n}{np^2}}$
of an eigenvalue of
![]() $\frac{1}{\sqrt{\alpha }} H_0$
, defined in (
1.2
).
$\frac{1}{\sqrt{\alpha }} H_0$
, defined in (
1.2
).
In the upcoming Section 2, it will be demonstrated that eigenvalues in the bulk of the distributions for
![]() $\frac{1}{\sqrt{\alpha }} H$
and for
$\frac{1}{\sqrt{\alpha }} H$
and for
![]() $\frac{1}{\sqrt{\alpha }} H_0$
have absolute value 1. Since
$\frac{1}{\sqrt{\alpha }} H_0$
have absolute value 1. Since
![]() $p\gg \frac{\log ^{2/3} n}{n^{1/6}}$
, we have
$p\gg \frac{\log ^{2/3} n}{n^{1/6}}$
, we have
![]() $R=40\sqrt{\frac{\log n}{np^2}}=o(1)$
, and consequently, Theorem 1.6 provides informative results. We would like to mention that the above result has been improved to hold for
$R=40\sqrt{\frac{\log n}{np^2}}=o(1)$
, and consequently, Theorem 1.6 provides informative results. We would like to mention that the above result has been improved to hold for
![]() $p \gg \log n/n$
and that each eigenvalue of
$p \gg \log n/n$
and that each eigenvalue of
![]() $\frac{1}{\sqrt{\alpha }} H$
is within distance
$\frac{1}{\sqrt{\alpha }} H$
is within distance
![]() $ O((\frac{\log n}{np})^{1/4})$
of an eigenvalue of
$ O((\frac{\log n}{np})^{1/4})$
of an eigenvalue of
![]() $\frac{1}{\sqrt{\alpha }} H_0$
, using a variant of Bauer-Fike perturbation theorem that appeared later in [Reference Coste and Zhu11, Corollary 2.4], as opposed to invoking the classical Bauer-Fike theorem in this paper (see Theorem 4.1).
$\frac{1}{\sqrt{\alpha }} H_0$
, using a variant of Bauer-Fike perturbation theorem that appeared later in [Reference Coste and Zhu11, Corollary 2.4], as opposed to invoking the classical Bauer-Fike theorem in this paper (see Theorem 4.1).
1.2 Outline
We will describe the ESD of the partly averaged matrix
![]() $H_0$
to prove Proposition 1.2 in Section 2. In Section 3, we will show that the ESDs of
$H_0$
to prove Proposition 1.2 in Section 2. In Section 3, we will show that the ESDs of
![]() $H$
and
$H$
and
![]() $H_0$
approach each other as
$H_0$
approach each other as
![]() $n$
goes to infinity by using the replacement principle [Reference Tao and Van34, Theorem 2.1] and in Section 4 we will use the Bauer-Fike theorem to prove Theorem 1.6, showing that the partly averaged matrix
$n$
goes to infinity by using the replacement principle [Reference Tao and Van34, Theorem 2.1] and in Section 4 we will use the Bauer-Fike theorem to prove Theorem 1.6, showing that the partly averaged matrix
![]() $H_0$
has eigenvalues close to those of
$H_0$
has eigenvalues close to those of
![]() $H$
in the limit as
$H$
in the limit as
![]() $n\to \infty$
.
$n\to \infty$
.
1.3 Background definitions
We give a few definitions to make clear the convergence described in Theorem 1.4 between empirical spectral distribution measures of
![]() $H$
and
$H$
and
![]() $H_0$
. For an
$H_0$
. For an
![]() $n\times n$
matrix
$n\times n$
matrix
![]() $M_n$
with eigenvalues
$M_n$
with eigenvalues
![]() $\lambda _1, \ldots, \lambda _n$
, the empirical spectral measure
$\lambda _1, \ldots, \lambda _n$
, the empirical spectral measure
![]() $\mu _{M_n}$
of
$\mu _{M_n}$
of
![]() $M_n$
is defined to be
$M_n$
is defined to be
where
![]() $\delta _x$
is the Dirac delta function with mass 1 at
$\delta _x$
is the Dirac delta function with mass 1 at
![]() $x$
. Note that
$x$
. Note that
![]() $\mu _{M_n}$
is a probability measure on the complex numbers
$\mu _{M_n}$
is a probability measure on the complex numbers
![]() $\mathbb C$
. The empirical spectral distribution (ESD) for
$\mathbb C$
. The empirical spectral distribution (ESD) for
![]() $M_n$
is defined to be
$M_n$
is defined to be
For
![]() $T$
a topological space (for example
$T$
a topological space (for example
![]() $\mathbb R$
or
$\mathbb R$
or
![]() $\mathbb C$
) and
$\mathbb C$
) and
![]() $\mathcal B$
its Borel
$\mathcal B$
its Borel
![]() $\sigma$
-field, we can define convergence of a sequence
$\sigma$
-field, we can define convergence of a sequence
![]() $(\mu _n)_{n \ge 1}$
of random probability measures on
$(\mu _n)_{n \ge 1}$
of random probability measures on
![]() $(T,\mathcal B)$
to a nonrandom probability measure
$(T,\mathcal B)$
to a nonrandom probability measure
![]() $\mu$
also on
$\mu$
also on
![]() $(T,\mathcal B)$
as follows. We say that
$(T,\mathcal B)$
as follows. We say that
![]() $\mu _n$
converges weakly to
$\mu _n$
converges weakly to
![]() $\mu$
in probability as
$\mu$
in probability as
![]() $n \to \infty$
(written
$n \to \infty$
(written
![]() $\mu _n \to \mu$
in probability) if for all bounded continuous functions
$\mu _n \to \mu$
in probability) if for all bounded continuous functions
![]() $f\;:\; T \to \mathbb R$
and all
$f\;:\; T \to \mathbb R$
and all
![]() $\epsilon >0$
we have
$\epsilon >0$
we have
Also, we say that
![]() $\mu _n$
converges weakly to
$\mu _n$
converges weakly to
![]() $\mu$
almost surely as
$\mu$
almost surely as
![]() $n \to \infty$
(written
$n \to \infty$
(written
![]() $\mu _n \to \mu$
a.s.) if for all bounded continuous functions
$\mu _n \to \mu$
a.s.) if for all bounded continuous functions
![]() $f\;:\;T \to \mathbb R$
, we have that
$f\;:\;T \to \mathbb R$
, we have that
![]() $\left \lvert{\int _T f \, d\mu _n - \int _T f\, d\mu }\right \rvert \to 0$
almost surely as
$\left \lvert{\int _T f \, d\mu _n - \int _T f\, d\mu }\right \rvert \to 0$
almost surely as
![]() $n \to \infty$
.
$n \to \infty$
.
We will use
![]() $\|A\|_F \;:\!=\; \textrm{tr} \; ( AA^*)^{1/2}$
to denote the Frobenius norm or Hilbert-Schmidt norm, and
$\|A\|_F \;:\!=\; \textrm{tr} \; ( AA^*)^{1/2}$
to denote the Frobenius norm or Hilbert-Schmidt norm, and
![]() $\left \|A\right \|$
to denote the operator norm. We denote
$\left \|A\right \|$
to denote the operator norm. We denote
![]() $\|A\|_{\max }=\max _{ij}|a_{ij}|$
. We use the notation
$\|A\|_{\max }=\max _{ij}|a_{ij}|$
. We use the notation
![]() $o(1)$
to denote a small quantity that tends to zero as
$o(1)$
to denote a small quantity that tends to zero as
![]() $n$
goes to infinity. We use the asymptotic notation
$n$
goes to infinity. We use the asymptotic notation
![]() $f(n)\ll g(n)$
if
$f(n)\ll g(n)$
if
![]() $f(n)/g(n)=o(1)$
and we write
$f(n)/g(n)=o(1)$
and we write
![]() $f(n)= o(g(n))$
; furthermore, we write
$f(n)= o(g(n))$
; furthermore, we write
![]() $f(n)=O(g(n))$
if
$f(n)=O(g(n))$
if
![]() $f(n)\le C g(n)$
for a constant
$f(n)\le C g(n)$
for a constant
![]() $C>0$
when
$C>0$
when
![]() $n$
is sufficiently large. Finally, we will use
$n$
is sufficiently large. Finally, we will use
![]() $I$
or
$I$
or
![]() $I_n$
to denote the identity matrix, where the subscript
$I_n$
to denote the identity matrix, where the subscript
![]() $n$
will be omitted when the dimension can be inferred by context.
$n$
will be omitted when the dimension can be inferred by context.
2. The spectrum of
 $H_0$
$H_0$
We are interested in the limiting ESD of
![]() $H$
when
$H$
when
![]() $H$
is scaled to have bounded support (except for one outlier eigenvalue), and so we will work with the following rescaled conjugation of
$H$
is scaled to have bounded support (except for one outlier eigenvalue), and so we will work with the following rescaled conjugation of
![]() $H$
, which has the same eigenvalues as
$H$
, which has the same eigenvalues as
![]() $H/\sqrt{\alpha }$
.
$H/\sqrt{\alpha }$
.
 \begin{equation*} \widetilde {H}\;:\!=\;\frac {1}{\sqrt {\alpha }}\left ( \begin {array}{c@{\quad}c} \frac {1}{\sqrt {\alpha }}I & 0\\[5pt] 0&I \end {array} \right ) \left ( \begin {array}{c@{\quad}c} A &I-D \\[5pt] I &0 \end {array} \right ) \left ( \begin {array}{c@{\quad}c} \sqrt {\alpha } I & 0\\[5pt] 0 &I \end {array} \right )= \left ( \begin {array}{c@{\quad}c} \frac {1}{\sqrt {\alpha }}A & \frac {1}{\alpha }(I-D) \\[5pt] I &0 \end {array} \right ). \end{equation*}
\begin{equation*} \widetilde {H}\;:\!=\;\frac {1}{\sqrt {\alpha }}\left ( \begin {array}{c@{\quad}c} \frac {1}{\sqrt {\alpha }}I & 0\\[5pt] 0&I \end {array} \right ) \left ( \begin {array}{c@{\quad}c} A &I-D \\[5pt] I &0 \end {array} \right ) \left ( \begin {array}{c@{\quad}c} \sqrt {\alpha } I & 0\\[5pt] 0 &I \end {array} \right )= \left ( \begin {array}{c@{\quad}c} \frac {1}{\sqrt {\alpha }}A & \frac {1}{\alpha }(I-D) \\[5pt] I &0 \end {array} \right ). \end{equation*}
Note that the diagonal matrix
![]() $\frac{1}{\alpha }(I-D)$
is equal to
$\frac{1}{\alpha }(I-D)$
is equal to
![]() $-I$
in expectation, and so we will compare the eigenvalues of
$-I$
in expectation, and so we will compare the eigenvalues of
![]() $\widetilde H$
to those of the partly averaged matrix
$\widetilde H$
to those of the partly averaged matrix
![]() $\widetilde H_0$
, noting that
$\widetilde H_0$
, noting that
![]() $\widetilde H = \widetilde H_0 + E$
, where
$\widetilde H = \widetilde H_0 + E$
, where
 \begin{equation} \widetilde H_0 \;:\!=\; \left ( \begin{array}{c@{\quad}c} \frac{1}{\sqrt{\alpha }} A & -I \\[5pt] I & 0 \end{array} \right )\qquad \mbox{ and } \qquad E\;:\!=\; \left ( \begin{array}{c@{\quad}c} 0 & I+\frac{1}{\alpha }(I-D) \\[5pt] 0 & 0 \end{array} \right ). \end{equation}
\begin{equation} \widetilde H_0 \;:\!=\; \left ( \begin{array}{c@{\quad}c} \frac{1}{\sqrt{\alpha }} A & -I \\[5pt] I & 0 \end{array} \right )\qquad \mbox{ and } \qquad E\;:\!=\; \left ( \begin{array}{c@{\quad}c} 0 & I+\frac{1}{\alpha }(I-D) \\[5pt] 0 & 0 \end{array} \right ). \end{equation}
Note that
![]() $H_0/\sqrt{\alpha }$
and
$H_0/\sqrt{\alpha }$
and
![]() $\widetilde H_0$
also have identical eigenvalues.
$\widetilde H_0$
also have identical eigenvalues.
We will show that
![]() $\widetilde H_0$
is explicitly diagonalizable in terms of the eigenvectors and eigenvalues of
$\widetilde H_0$
is explicitly diagonalizable in terms of the eigenvectors and eigenvalues of
![]() $\frac{1}{\sqrt{\alpha }} A$
, and then use this information to find an explicit form for the characteristic polynomial for
$\frac{1}{\sqrt{\alpha }} A$
, and then use this information to find an explicit form for the characteristic polynomial for
![]() $\widetilde H_0$
.
$\widetilde H_0$
.
2.1 Spectrum of
 $\widetilde H_0$
: proof of Proposition 1.2
$\widetilde H_0$
: proof of Proposition 1.2
Since
![]() $\frac{1}{\sqrt{\alpha }} A$
is a real symmetric matrix, it has a set
$\frac{1}{\sqrt{\alpha }} A$
is a real symmetric matrix, it has a set
![]() $v_1,\ldots, v_n$
of orthonormal eigenvectors with corresponding real eigenvalues
$v_1,\ldots, v_n$
of orthonormal eigenvectors with corresponding real eigenvalues
![]() $\lambda _1 \ge \lambda _2 \ge \ldots \ge \lambda _n$
. Thus we may write
$\lambda _1 \ge \lambda _2 \ge \ldots \ge \lambda _n$
. Thus we may write
![]() $\frac{A}{\sqrt \alpha } = U^{T}{\textrm{diag}}(\lambda _1,\ldots,\lambda _n) U$
where
$\frac{A}{\sqrt \alpha } = U^{T}{\textrm{diag}}(\lambda _1,\ldots,\lambda _n) U$
where
![]() $U$
is an orthogonal matrix. Consider the matrix
$U$
is an orthogonal matrix. Consider the matrix
![]() $xI - \widetilde H_0$
, and note that
$xI - \widetilde H_0$
, and note that
 \begin{equation*} \begin {pmatrix} I & 0\\[5pt] -xI & I \end {pmatrix} (xI - \widetilde H_0) = \begin {pmatrix} xI-\frac {1}{\sqrt \alpha } A & I\\[5pt] -x\big (xI-\frac {1}{\sqrt \alpha } A\big ) -I & 0 \end {pmatrix}, \end{equation*}
\begin{equation*} \begin {pmatrix} I & 0\\[5pt] -xI & I \end {pmatrix} (xI - \widetilde H_0) = \begin {pmatrix} xI-\frac {1}{\sqrt \alpha } A & I\\[5pt] -x\big (xI-\frac {1}{\sqrt \alpha } A\big ) -I & 0 \end {pmatrix}, \end{equation*}
we see that
![]() $\det (xI-\widetilde H_0) = \det (I + x(xI - \frac{1}{\sqrt{\alpha }} A) ) = \det (x^2 I - \frac{x}{\sqrt{\alpha }} A + I)$
. Conjugating to diagonalize
$\det (xI-\widetilde H_0) = \det (I + x(xI - \frac{1}{\sqrt{\alpha }} A) ) = \det (x^2 I - \frac{x}{\sqrt{\alpha }} A + I)$
. Conjugating to diagonalize
![]() $A$
, we see that
$A$
, we see that
With the characteristic polynomial for
![]() $\widetilde H_0$
factored into quadratics as in (2.2), we see that for each
$\widetilde H_0$
factored into quadratics as in (2.2), we see that for each
![]() $\lambda _i$
of
$\lambda _i$
of
![]() $\frac{1}{\sqrt{\alpha }} A$
, there are two eigenvalues
$\frac{1}{\sqrt{\alpha }} A$
, there are two eigenvalues
![]() $\mu _{2i-1}$
and
$\mu _{2i-1}$
and
![]() $\mu _{2i}$
for
$\mu _{2i}$
for
![]() $\widetilde H_0$
which are the two solutions to
$\widetilde H_0$
which are the two solutions to
![]() $x^2-\lambda _i x +1=0$
; thus,
$x^2-\lambda _i x +1=0$
; thus,
 \begin{equation} \mu _{2i-1} = \frac{\lambda _i + \sqrt{ \lambda _i^2 - 4}}{2} \qquad \mbox{ and } \qquad \mu _{2i} = \frac{\lambda _i - \sqrt{ \lambda _i^2 - 4}}{2}. \end{equation}
\begin{equation} \mu _{2i-1} = \frac{\lambda _i + \sqrt{ \lambda _i^2 - 4}}{2} \qquad \mbox{ and } \qquad \mu _{2i} = \frac{\lambda _i - \sqrt{ \lambda _i^2 - 4}}{2}. \end{equation}
The eigenvalues of
![]() $A$
are well-understood. We use the following results that exist in literature.
$A$
are well-understood. We use the following results that exist in literature.
Theorem 2.1 ([Reference Krivelevich and Sudakov26, Reference Lee and Schnelli27]). Let
![]() $A$
be the adjacency matrix for an Erdős-Rényi random graph
$A$
be the adjacency matrix for an Erdős-Rényi random graph
![]() $G(n,p)$
. Assume
$G(n,p)$
. Assume
![]() $0< p\le p_0<1$
for a constant
$0< p\le p_0<1$
for a constant
![]() $p_0$
and
$p_0$
and
![]() $p\ge n^{-1+\phi }$
for a small constant
$p\ge n^{-1+\phi }$
for a small constant
![]() $\phi >0$
. Then for any
$\phi >0$
. Then for any
![]() $\epsilon >0$
, the following holds with probability
$\epsilon >0$
, the following holds with probability
![]() $1-o(1)$
:
$1-o(1)$
:
where
![]() $L=2+ \frac{s^{(4)}}{np} + O(\frac{1}{(np)^2})$
and
$L=2+ \frac{s^{(4)}}{np} + O(\frac{1}{(np)^2})$
and
![]() $s^{(4)} =n^2p \left [ \frac{p^3 + (1-p)^3}{n^2 p(1-p)}-\frac{3}{n^2}\right ].$
$s^{(4)} =n^2p \left [ \frac{p^3 + (1-p)^3}{n^2 p(1-p)}-\frac{3}{n^2}\right ].$
Proof. We collect relevant results regarding the eigenvalues of
![]() $A$
from different works in the literature. In [Reference Krivelevich and Sudakov26], it is shown that with probability
$A$
from different works in the literature. In [Reference Krivelevich and Sudakov26], it is shown that with probability
![]() $1-o(1)$
,
$1-o(1)$
,
![]() $\lambda _1(A) = (1+o(1))\max \{np, \sqrt{\Delta } \}$
where
$\lambda _1(A) = (1+o(1))\max \{np, \sqrt{\Delta } \}$
where
![]() $\Delta$
is the maximum degree. As long as
$\Delta$
is the maximum degree. As long as
![]() $np/\log n \to \infty$
,
$np/\log n \to \infty$
,
![]() $\max \{np, \sqrt{\Delta } \} = np$
(for the bounds on
$\max \{np, \sqrt{\Delta } \} = np$
(for the bounds on
![]() $\Delta$
see, for instance, the proof of Lemma 3.5 below).
$\Delta$
see, for instance, the proof of Lemma 3.5 below).
The operator norm of
![]() $A-{\mathbb E } A$
and the extreme eigenvalues of
$A-{\mathbb E } A$
and the extreme eigenvalues of
![]() $A$
have been studied in various works (see [Reference Benaych-Georges, Bordenave and Knowles5, Reference Erdős, Knowles, Yau and Yin12, Reference Füredi and Komlós13, Reference He and Knowles18, Reference Huang, Landon and Yau21, Reference Lee and Schnelli27, Reference Vu36]). In particular, in [Reference Lee and Schnelli27, Theorem 2.9], assuming
$A$
have been studied in various works (see [Reference Benaych-Georges, Bordenave and Knowles5, Reference Erdős, Knowles, Yau and Yin12, Reference Füredi and Komlós13, Reference He and Knowles18, Reference Huang, Landon and Yau21, Reference Lee and Schnelli27, Reference Vu36]). In particular, in [Reference Lee and Schnelli27, Theorem 2.9], assuming
![]() $p\ge n^{-1 + \phi }$
, the authors proved that for any
$p\ge n^{-1 + \phi }$
, the authors proved that for any
![]() $\epsilon >0$
and
$\epsilon >0$
and
![]() $C>0$
, the following estimate holds with probability at least
$C>0$
, the following estimate holds with probability at least
![]() $1-n^{-C}$
:
$1-n^{-C}$
:
 \begin{equation*}\left | \frac {1}{\sqrt {np(1-p)}} \| A - {\mathbb E } A \| -L \right | \le n^{\epsilon } \left (\frac {1}{(np)^2} + \frac {1}{n^{2/3}} \right )\end{equation*}
\begin{equation*}\left | \frac {1}{\sqrt {np(1-p)}} \| A - {\mathbb E } A \| -L \right | \le n^{\epsilon } \left (\frac {1}{(np)^2} + \frac {1}{n^{2/3}} \right )\end{equation*}
with
![]() $L=2+ \frac{s^{(4)}}{np} + O(\frac{1}{(np)^2})$
and
$L=2+ \frac{s^{(4)}}{np} + O(\frac{1}{(np)^2})$
and
![]() $s^{(4)} =n^2p \left [ \frac{p^3 + (1-p)^3}{n^2 p(1-p)}-\frac{3}{n^2}\right ] = 1+ O(p).$
The conclusion of the theorem follows immediately from the classical Weyl’s inequality that
$s^{(4)} =n^2p \left [ \frac{p^3 + (1-p)^3}{n^2 p(1-p)}-\frac{3}{n^2}\right ] = 1+ O(p).$
The conclusion of the theorem follows immediately from the classical Weyl’s inequality that
![]() $\max _{2\le i \le n}|\lambda _i(A)+p|=\max _{2\le i \le n}|\lambda _i(A)-\lambda _i({\mathbb E } A)|\le \|A-{\mathbb E } A\|$
.
$\max _{2\le i \le n}|\lambda _i(A)+p|=\max _{2\le i \le n}|\lambda _i(A)-\lambda _i({\mathbb E } A)|\le \|A-{\mathbb E } A\|$
.
Now we are ready to derive Proposition 1.2.
Proof of Proposition
1.2. Note that
![]() $\lambda _i=\lambda _i(A)/\sqrt{\alpha }$
and
$\lambda _i=\lambda _i(A)/\sqrt{\alpha }$
and
![]() $\alpha =(n-1)p-1$
. We have that
$\alpha =(n-1)p-1$
. We have that
with probability
![]() $1-o(1)$
by Theorem 2.1. Therefore, for
$1-o(1)$
by Theorem 2.1. Therefore, for
![]() $\lambda _1$
, we see from (2.3) that
$\lambda _1$
, we see from (2.3) that
![]() $\mu _1, \mu _2$
are real eigenvalues and
$\mu _1, \mu _2$
are real eigenvalues and
with probability
![]() $1-o(1)$
. Next, by Theorem 2.1, it holds with probability
$1-o(1)$
. Next, by Theorem 2.1, it holds with probability
![]() $1-o(1)$
for any
$1-o(1)$
for any
![]() $2\le i \le n$
that
$2\le i \le n$
that
Since
![]() $p \ge C/\sqrt{n}$
for a sufficiently large constant
$p \ge C/\sqrt{n}$
for a sufficiently large constant
![]() $C$
, we have
$C$
, we have
 \begin{align*} \lambda _i^2 &\le \frac{1}{\alpha } \left [ 2\sqrt{np(1-p)}+ O(\max \{p,(np)^{-1/2}, p^{1/2} n^{-1/6+\epsilon }\}) \right ]^2\\[5pt] &=\frac{4 np (1-p) + O(\max \{p \sqrt{np},1, pn^{1/3 + \epsilon }\})}{np-(p+1)}\\[5pt] &=\frac{4 (1-p) + O(\max \{\sqrt{p/n},(np)^{-1}, n^{-2/3 + \epsilon }\})}{1-\frac{p+1}{np}} \\[5pt] &= 4(1-p)+O\left (\max \{\sqrt{p/n},(np)^{-1}, n^{-2/3 + \epsilon }\}\right ) + O\left (\frac{1}{np}\right )\le 4-3p, \end{align*}
\begin{align*} \lambda _i^2 &\le \frac{1}{\alpha } \left [ 2\sqrt{np(1-p)}+ O(\max \{p,(np)^{-1/2}, p^{1/2} n^{-1/6+\epsilon }\}) \right ]^2\\[5pt] &=\frac{4 np (1-p) + O(\max \{p \sqrt{np},1, pn^{1/3 + \epsilon }\})}{np-(p+1)}\\[5pt] &=\frac{4 (1-p) + O(\max \{\sqrt{p/n},(np)^{-1}, n^{-2/3 + \epsilon }\})}{1-\frac{p+1}{np}} \\[5pt] &= 4(1-p)+O\left (\max \{\sqrt{p/n},(np)^{-1}, n^{-2/3 + \epsilon }\}\right ) + O\left (\frac{1}{np}\right )\le 4-3p, \end{align*}
for all sufficiently large
![]() $n$
. Hence, for all
$n$
. Hence, for all
![]() $i\ge 2$
, we have
$i\ge 2$
, we have
![]() $\lambda _i^2 <4$
and thus
$\lambda _i^2 <4$
and thus
![]() $\mu _{2i-1}, \mu _{2i}$
are complex eigenvalues with magnitude
$\mu _{2i-1}, \mu _{2i}$
are complex eigenvalues with magnitude
![]() $1$
(since
$1$
(since
![]() $|\mu _{2i-1}|=|\mu _{2i}|=1$
). One should also note that
$|\mu _{2i-1}|=|\mu _{2i}|=1$
). One should also note that
![]() $\mu _{2i-1}\mu _{2i} = 1$
for every
$\mu _{2i-1}\mu _{2i} = 1$
for every
![]() $i$
, and that whenever
$i$
, and that whenever
![]() $\mu _{2i-1}$
is complex (i.e.,
$\mu _{2i-1}$
is complex (i.e.,
![]() $i\ge 2$
), its complex conjugate is
$i\ge 2$
), its complex conjugate is
![]() $\overline \mu _{2i-1}=\mu _{2i}$
.
$\overline \mu _{2i-1}=\mu _{2i}$
.
Furthermore, note that
![]() ${\mathsf{Re}}\mu _{2i-1}={\mathsf{Re}} \mu _{2i} =\lambda _i/2 = \lambda _i(A)/2\sqrt{\alpha }$
. It is known that the empirical spectral measure of
${\mathsf{Re}}\mu _{2i-1}={\mathsf{Re}} \mu _{2i} =\lambda _i/2 = \lambda _i(A)/2\sqrt{\alpha }$
. It is known that the empirical spectral measure of
![]() $A/\sqrt{np(1-p)}$
converges to the semicircular law supported on
$A/\sqrt{np(1-p)}$
converges to the semicircular law supported on
![]() $[-2,2]$
assuming
$[-2,2]$
assuming
![]() $np\to \infty$
(see for instance [Reference Khorunzhy and Pastur25] or [Reference Tran, Van and Wang35]). We have the ESD of the scaled real parts of
$np\to \infty$
(see for instance [Reference Khorunzhy and Pastur25] or [Reference Tran, Van and Wang35]). We have the ESD of the scaled real parts of
![]() $\mu _j$
$\mu _j$
 \begin{equation*}\frac {1}{2n}\sum _{j=1}^{2n} \delta _{\frac {2{\mathsf {Re}}\mu _{j}}{\sqrt {1-p}}} \to \mu _{\text{sc}}\end{equation*}
\begin{equation*}\frac {1}{2n}\sum _{j=1}^{2n} \delta _{\frac {2{\mathsf {Re}}\mu _{j}}{\sqrt {1-p}}} \to \mu _{\text{sc}}\end{equation*}
weakly almost surely where
![]() $\mu _{\text{sc}}$
is the semicircular law supported on
$\mu _{\text{sc}}$
is the semicircular law supported on
![]() $[-2,2]$
. The proof of Proposition 1.2 is now complete.
$[-2,2]$
. The proof of Proposition 1.2 is now complete.
2.2 Real eigenvalues of
 $\widetilde H_0$
when
$\widetilde H_0$
when
 $p\le n^{-1/2}$
$p\le n^{-1/2}$
As mentioned in Remark 1.3, when
![]() $p$
becomes smaller than
$p$
becomes smaller than
![]() $n^{-1/2}$
, more real eigenvalues of
$n^{-1/2}$
, more real eigenvalues of
![]() $\widetilde H_0$
will emerge. We can identify some of these eigenvalues, using recent results of [Reference Erdős, Knowles, Yau and Yin12, Reference He and Knowles18, Reference Huang, Landon and Yau21, Reference Lee and Schnelli27] in the study of the extreme eigenvalues of
$\widetilde H_0$
will emerge. We can identify some of these eigenvalues, using recent results of [Reference Erdős, Knowles, Yau and Yin12, Reference He and Knowles18, Reference Huang, Landon and Yau21, Reference Lee and Schnelli27] in the study of the extreme eigenvalues of
![]() $A$
. For instance, in [Reference Lee and Schnelli27, Corollary 2.13], assume
$A$
. For instance, in [Reference Lee and Schnelli27, Corollary 2.13], assume
![]() $n^{2\phi -1} \le p \le n^{-2\phi '}$
for
$n^{2\phi -1} \le p \le n^{-2\phi '}$
for
![]() $\phi >1/6$
and
$\phi >1/6$
and
![]() $\phi '>0$
. Then
$\phi '>0$
. Then
 \begin{align} \lim _{n\to \infty }{\mathbb{P}}\left ( n^{2/3} \Big (\frac{1}{\sqrt{np(1-p)}}\lambda _2(A) - \mathcal L -a \Big )\le s\right ) = F_{1}^{\text{TW}}(s), \end{align}
\begin{align} \lim _{n\to \infty }{\mathbb{P}}\left ( n^{2/3} \Big (\frac{1}{\sqrt{np(1-p)}}\lambda _2(A) - \mathcal L -a \Big )\le s\right ) = F_{1}^{\text{TW}}(s), \end{align}
where
![]() $\mathcal L= 2+\frac{1}{np} + O(\frac{1}{n^2p^2})$
,
$\mathcal L= 2+\frac{1}{np} + O(\frac{1}{n^2p^2})$
,
![]() $a=\sqrt{\frac{p}{n(1-p)}}$
and
$a=\sqrt{\frac{p}{n(1-p)}}$
and
![]() $F_1^{\text{TW}}(s)$
is the Tracy-Widom distribution function. Therefore, when
$F_1^{\text{TW}}(s)$
is the Tracy-Widom distribution function. Therefore, when
![]() $p\ge n^{-2/3+\epsilon }$
, by noting that
$p\ge n^{-2/3+\epsilon }$
, by noting that
![]() $F_1^{\text{TW}}(s) \to 1$
as
$F_1^{\text{TW}}(s) \to 1$
as
![]() $s\to \infty$
and selecting
$s\to \infty$
and selecting
![]() $s$
to be a large constant in (2.5), we see that
$s$
to be a large constant in (2.5), we see that
 \begin{equation*}\lambda _2(A) = 2\sqrt {np(1-p)} + p + \sqrt {\frac {1-p}{np}} + O\left (\frac {\sqrt {np}}{n^{2/3}}\right ).\end{equation*}
\begin{equation*}\lambda _2(A) = 2\sqrt {np(1-p)} + p + \sqrt {\frac {1-p}{np}} + O\left (\frac {\sqrt {np}}{n^{2/3}}\right ).\end{equation*}
Note that if
![]() $p<\frac{1-p}{n^{1/3}}$
, then
$p<\frac{1-p}{n^{1/3}}$
, then
![]() $p<\sqrt{\frac{1-p}{np}}$
and thus for
$p<\sqrt{\frac{1-p}{np}}$
and thus for
![]() $ n^{-2/3+\epsilon }\le p \le n^{-1/2}\ll n^{-1/3}$
,
$ n^{-2/3+\epsilon }\le p \le n^{-1/2}\ll n^{-1/3}$
,
 \begin{align*} \lambda _2^2 -4 &= \left (\frac{\lambda _2(A)}{\sqrt \alpha } \right )^2-4 = \frac{\left (2\sqrt{np(1-p)} + \sqrt{\frac{1-p}{np}} +p+ O\big (\frac{\sqrt{np}}{n^{2/3}} \big ) \right )^2}{np-(p+1)}-4\\[5pt] &= \frac{\left (2\sqrt{np(1-p)} + \sqrt{\frac{1-p}{np}} +p \right )^2+O\left (\frac{np}{n^{2/3}} \right )}{np-(p+1)}-4\\[5pt] &= \frac{4np(1-p) + 4(1-p) + 4p\sqrt{np(1-p)}+O(\frac{np}{n^{2/3}})}{np-(p+1)}-4\\[5pt] &=\frac{4(1-p) +\frac{4(1-p)}{np} + 4p \sqrt{\frac{1-p}{np}}+O\left (\frac{1}{n^{2/3}} \right )}{1-\frac{p+1}{np}}-4\\[5pt] &=-4p + 4p \sqrt{\frac{1-p}{np}}+ \frac{4(1-p)(2+p)}{np} +O(n^{-2/3}) > 0. \end{align*}
\begin{align*} \lambda _2^2 -4 &= \left (\frac{\lambda _2(A)}{\sqrt \alpha } \right )^2-4 = \frac{\left (2\sqrt{np(1-p)} + \sqrt{\frac{1-p}{np}} +p+ O\big (\frac{\sqrt{np}}{n^{2/3}} \big ) \right )^2}{np-(p+1)}-4\\[5pt] &= \frac{\left (2\sqrt{np(1-p)} + \sqrt{\frac{1-p}{np}} +p \right )^2+O\left (\frac{np}{n^{2/3}} \right )}{np-(p+1)}-4\\[5pt] &= \frac{4np(1-p) + 4(1-p) + 4p\sqrt{np(1-p)}+O(\frac{np}{n^{2/3}})}{np-(p+1)}-4\\[5pt] &=\frac{4(1-p) +\frac{4(1-p)}{np} + 4p \sqrt{\frac{1-p}{np}}+O\left (\frac{1}{n^{2/3}} \right )}{1-\frac{p+1}{np}}-4\\[5pt] &=-4p + 4p \sqrt{\frac{1-p}{np}}+ \frac{4(1-p)(2+p)}{np} +O(n^{-2/3}) > 0. \end{align*}
Hence, from (2.3), both
![]() $\mu _3$
and
$\mu _3$
and
![]() $\mu _4$
are real. The convergence result (2.5) holds for finitely many extreme eigenvalues of
$\mu _4$
are real. The convergence result (2.5) holds for finitely many extreme eigenvalues of
![]() $A$
and thus they also generate real eigenvalues for
$A$
and thus they also generate real eigenvalues for
![]() $\widetilde H_0$
.
$\widetilde H_0$
.
The fluctuation of the extreme eigenvalues of
![]() $A$
has been obtained in [Reference Huang, Landon and Yau21, Corollary 1.5] for
$A$
has been obtained in [Reference Huang, Landon and Yau21, Corollary 1.5] for
![]() $n^{-7/9} \ll p \ll n^{-2/3}$
and in [Reference He and Knowles18] for the remaining range of
$n^{-7/9} \ll p \ll n^{-2/3}$
and in [Reference He and Knowles18] for the remaining range of
![]() $p$
up to
$p$
up to
![]() $p\ge n^{-1+\epsilon }$
. One could use similar discussion as above to extract information about the real eigenvalues of
$p\ge n^{-1+\epsilon }$
. One could use similar discussion as above to extract information about the real eigenvalues of
![]() $\widetilde H_0$
. The details are omitted.
$\widetilde H_0$
. The details are omitted.
2.3
 $\widetilde H_0$
is diagonalizable
$\widetilde H_0$
is diagonalizable
We can now demonstrate an explicit diagonalization for
![]() $\widetilde H_0$
. Since
$\widetilde H_0$
. Since
![]() $\mu _{2i-1}$
and
$\mu _{2i-1}$
and
![]() $\mu _{2i}$
are solutions to
$\mu _{2i}$
are solutions to
![]() $\mu ^2-\mu \lambda _i +1=0$
, one can check that the following vectors
$\mu ^2-\mu \lambda _i +1=0$
, one can check that the following vectors
satisfy
![]() $y_{2i-1}^* \widetilde H_0 = \mu _{2i-1} y_{2i-1}^*$
and
$y_{2i-1}^* \widetilde H_0 = \mu _{2i-1} y_{2i-1}^*$
and
![]() $y_{2i}^* \widetilde H_0 = \mu _{2i} y_{2i}^*$
for all
$y_{2i}^* \widetilde H_0 = \mu _{2i} y_{2i}^*$
for all
![]() $i$
. Furthermore,
$i$
. Furthermore,
![]() $y_{2i-1}$
and
$y_{2i-1}$
and
![]() $y_{2i}$
are unit vectors. For
$y_{2i}$
are unit vectors. For
![]() $1\le i\le n$
, define the vectors
$1\le i\le n$
, define the vectors
 \begin{equation} x_{2i-1}=\frac{\sqrt{1+|\mu _{2i-1}|^2}}{\mu _{2i}-\mu _{2i-1}}\begin{pmatrix} v_i \\[5pt] \mu _{2i} v_i \end{pmatrix} \quad \text{ and }\quad x_{2i}=\frac{\sqrt{1+|\mu _{2i}|^2}}{\mu _{2i-1}-\mu _{2i}}\begin{pmatrix} v_i \\[5pt] \mu _{2i-1}v_i \end{pmatrix}\!. \end{equation}
\begin{equation} x_{2i-1}=\frac{\sqrt{1+|\mu _{2i-1}|^2}}{\mu _{2i}-\mu _{2i-1}}\begin{pmatrix} v_i \\[5pt] \mu _{2i} v_i \end{pmatrix} \quad \text{ and }\quad x_{2i}=\frac{\sqrt{1+|\mu _{2i}|^2}}{\mu _{2i-1}-\mu _{2i}}\begin{pmatrix} v_i \\[5pt] \mu _{2i-1}v_i \end{pmatrix}\!. \end{equation}
Defining
 \begin{equation*} Y=\begin{pmatrix} y_1^*\\[5pt] y_2^*\\[5pt] \vdots \\[5pt] y_{2n}^* \end{pmatrix} \quad \mbox{ and }\quad X=\begin{pmatrix} x_1, x_2, \ldots, x_{2n} \end{pmatrix} \end{equation*}
\begin{equation*} Y=\begin{pmatrix} y_1^*\\[5pt] y_2^*\\[5pt] \vdots \\[5pt] y_{2n}^* \end{pmatrix} \quad \mbox{ and }\quad X=\begin{pmatrix} x_1, x_2, \ldots, x_{2n} \end{pmatrix} \end{equation*}
we see that
![]() $X=Y^{-1}$
since
$X=Y^{-1}$
since
![]() $v_1,\ldots,v_n$
are orthonormal. Also it is easy to check that
$v_1,\ldots,v_n$
are orthonormal. Also it is easy to check that
![]() $Y\widetilde H_0 X = \text{diag}(\mu _1,\ldots,\mu _{2n})$
.
$Y\widetilde H_0 X = \text{diag}(\mu _1,\ldots,\mu _{2n})$
.
3. The bulk distribution: proving Theorem 1.4
We begin by re-stating Theorem 1.4 using the conjugated matrices defined in (2.1).
Theorem 3.1.
Let
![]() $A$
be the adjacency matrix for an Erdős-Rényi random graph
$A$
be the adjacency matrix for an Erdős-Rényi random graph
![]() $G(n,p)$
. Assume
$G(n,p)$
. Assume
![]() $0< p\le p_0<1$
for a constant
$0< p\le p_0<1$
for a constant
![]() $p_0$
and
$p_0$
and
![]() $np/\log n \to \infty$
with
$np/\log n \to \infty$
with
![]() $n$
. Let
$n$
. Let
![]() $\widetilde H$
be the rescaled conjugation of the non-backtracking spectrum operator for
$\widetilde H$
be the rescaled conjugation of the non-backtracking spectrum operator for
![]() $A$
defined in (
2.1
), and let
$A$
defined in (
2.1
), and let
![]() $\widetilde H_0$
be its partial derandomization, also defined in (
2.1
). Then,
$\widetilde H_0$
be its partial derandomization, also defined in (
2.1
). Then,
![]() $\mu _{\widetilde H} - \mu _{\widetilde H_0}$
converges almost surely (thus, also in probability) to zero as
$\mu _{\widetilde H} - \mu _{\widetilde H_0}$
converges almost surely (thus, also in probability) to zero as
![]() $n$
goes to infinity.
$n$
goes to infinity.
To prove Theorem 3.1, we will show that the bulk distribution of
![]() $\widetilde H$
matches that of
$\widetilde H$
matches that of
![]() $\widetilde H_0$
using the replacement principle [Reference Tao and Van34, Theorem 2.1], which we rephrase slightly as a perturbation result below (see Theorem 3.2). First, we give a few definitions that we will use throughout this section. We say that a random variable
$\widetilde H_0$
using the replacement principle [Reference Tao and Van34, Theorem 2.1], which we rephrase slightly as a perturbation result below (see Theorem 3.2). First, we give a few definitions that we will use throughout this section. We say that a random variable
![]() $X_n \in \mathbb C$
is bounded in probability if
$X_n \in \mathbb C$
is bounded in probability if
and we say that
![]() $X_n$
is almost surely bounded if
$X_n$
is almost surely bounded if
Theorem 3.2 (Replacement principle [Reference Tao and Van34]). Suppose for each
![]() $m$
that
$m$
that
![]() $M_m$
and
$M_m$
and
![]() $M_m+P_m$
are random
$M_m+P_m$
are random
![]() $m \times m$
matrices with entries in the complex numbers. Assume that
$m \times m$
matrices with entries in the complex numbers. Assume that
and that, for almost all complex numbers
![]() $z \in \mathbb C$
,
$z \in \mathbb C$
,
converges in probability (resp., almost surely) to zero; in particular, this second condition requires that for almost all
![]() $z \in \mathbb C$
, the matrices
$z \in \mathbb C$
, the matrices
![]() $M_m+P_m - zI$
and
$M_m+P_m - zI$
and
![]() $M_m - zI$
have non-zero determinant with probability
$M_m - zI$
have non-zero determinant with probability
![]() $1-o(1)$
(resp., almost surely non-zero for all but finitely many
$1-o(1)$
(resp., almost surely non-zero for all but finitely many
![]() $m$
).
$m$
).
Then
![]() $\mu _{M_m} - \mu _{M_m+P_m}$
converges in probability (resp., almost surely) to zero.
$\mu _{M_m} - \mu _{M_m+P_m}$
converges in probability (resp., almost surely) to zero.
Note that there is no independence assumption anywhere in Theorem 3.2; thus, entries in
![]() $P_m$
may depend on entries in
$P_m$
may depend on entries in
![]() $M_m$
and vice versa.
$M_m$
and vice versa.
We will use the following corollary of Theorem 3.2, which essentially says that if the perturbation
![]() $P_m$
has largest singular value of order less than the smallest singular value for
$P_m$
has largest singular value of order less than the smallest singular value for
![]() $M_m-zI$
for almost every
$M_m-zI$
for almost every
![]() $z\in \mathbb C$
, then adding the perturbation
$z\in \mathbb C$
, then adding the perturbation
![]() $P_m$
does not appreciably change the bulk distribution of
$P_m$
does not appreciably change the bulk distribution of
![]() $M_m$
.
$M_m$
.
Corollary 3.3.
For each
![]() $m$
, let
$m$
, let
![]() $M_m$
and
$M_m$
and
![]() $P_m$
be random
$P_m$
be random
![]() $m\times m$
matrices with entries in the complex numbers, and let
$m\times m$
matrices with entries in the complex numbers, and let
![]() $f(z,m)\ge 1$
be a real function depending on
$f(z,m)\ge 1$
be a real function depending on
![]() $z$
and
$z$
and
![]() $m$
. Assume that
$m$
. Assume that
and
and, for almost every complex number
![]() $z \in \mathbb C$
,
$z \in \mathbb C$
,
with probability tending to 1 (resp., almost surely for all but finitely many
![]() $m$
).
$m$
).
Then
![]() $\mu _{M_m} - \mu _{M_m+P_m}$
converges in probability (resp., almost surely) to zero.
$\mu _{M_m} - \mu _{M_m+P_m}$
converges in probability (resp., almost surely) to zero.
Proof. We will show that the three conditions (3.3), (3.4), and (3.5) of Corollary 3.3 together imply the two conditions needed to apply Theorem 3.2.
First note that (3.3) is identical to the first condition (3.1) of Theorem 3.2. Next, we will show in the remainder of the proof that condition (3.2) of Theorem 3.2 holds by noting that sufficiently small perturbations have a small effect on the singular values, and also the absolute value of the determinant is equal to the product of the singular values.
Let
![]() $z$
be a complex number for which (3.5) holds, let
$z$
be a complex number for which (3.5) holds, let
![]() $M_m-zI$
have singular values
$M_m-zI$
have singular values
![]() $\sigma _1 \ge \ldots \ge \sigma _m$
, and let
$\sigma _1 \ge \ldots \ge \sigma _m$
, and let
![]() $M_m+P_m-zI$
have singular values
$M_m+P_m-zI$
have singular values
![]() $\sigma _1+s_1 \ge \sigma _2+s_2 \ge \ldots \ge \sigma _m+s_m$
. We will use the following result, which is sometimes called Weyl’s perturbation theorem for singular values, to show that the
$\sigma _1+s_1 \ge \sigma _2+s_2 \ge \ldots \ge \sigma _m+s_m$
. We will use the following result, which is sometimes called Weyl’s perturbation theorem for singular values, to show that the
![]() $s_i$
are small.
$s_i$
are small.
Lemma 3.4 ([Reference Chafaï9, Theorem 1.3]). Let
![]() $A$
and
$A$
and
![]() $B$
be
$B$
be
![]() $m\times n$
real or complex matrices with singular values
$m\times n$
real or complex matrices with singular values
![]() $\sigma _1(A)\ge \ldots \ge \sigma _{\min \{m, n\}}(A) \ge 0$
and
$\sigma _1(A)\ge \ldots \ge \sigma _{\min \{m, n\}}(A) \ge 0$
and
![]() $\sigma _1(B)\ge \ldots \ge \sigma _{\min \{m, n\}}(B) \ge 0$
, respectively. Then
$\sigma _1(B)\ge \ldots \ge \sigma _{\min \{m, n\}}(B) \ge 0$
, respectively. Then
We then have that
and by (3.5),
which converges to zero in probability (resp., almost surely) by (3.4). Thus we know that
where the inequalities hold with probability tending to 1 (resp., almost surely for all sufficiently large
![]() $m$
). Using the fact that the absolute value of the determinant is the product of the singular values, we may write (3.2) as
$m$
). Using the fact that the absolute value of the determinant is the product of the singular values, we may write (3.2) as
 \begin{align*} \left |\frac{1}{m} \left (\log \prod _{i=1}^m (\sigma _i+s_i)- \log \prod _{i=1}^m\sigma _i\right ) \right | &= \frac{1}{m} \left | \sum _{i=1}^m \log \left ( 1+\frac{s_i}{\sigma _i}\right )\right | \le 2f(z,m)\|P_m\|, \end{align*}
\begin{align*} \left |\frac{1}{m} \left (\log \prod _{i=1}^m (\sigma _i+s_i)- \log \prod _{i=1}^m\sigma _i\right ) \right | &= \frac{1}{m} \left | \sum _{i=1}^m \log \left ( 1+\frac{s_i}{\sigma _i}\right )\right | \le 2f(z,m)\|P_m\|, \end{align*}
which converges to zero in probability (resp., almost surely) by (3.4). Thus, we have shown that (3.1) and (3.2) hold, which completes the proof.
3.1 Proof of Theorem 3.1
The proof of Theorem 3.1 will follow from Corollary 3.3 combined with lemmas showing that the conditions (3.3), (3.4), and (3.5) of Corollary 3.3 are satisfied. Indeed, Lemma 3.7 verifies (3.3), Lemma 3.9 verifies (3.5) and (3.4) follows by combining Lemma 3.5 and Lemma 3.9. Note that the assumption
![]() $np/\log n \to \infty$
in Theorem 3.1 is only needed to prove conditions (3.3) and (3.4). Condition (3.5) in fact follows for any
$np/\log n \to \infty$
in Theorem 3.1 is only needed to prove conditions (3.3) and (3.4). Condition (3.5) in fact follows for any
![]() $p$
and for more general matrices – see the proof of Lemma 3.9.
$p$
and for more general matrices – see the proof of Lemma 3.9.
In Corollary 3.3, we will take
![]() $M_m$
to be the partly derandomized matrix
$M_m$
to be the partly derandomized matrix
![]() $\widetilde H_0$
and
$\widetilde H_0$
and
![]() $P_m$
to be the matrix
$P_m$
to be the matrix
![]() $E$
[see (2.1)], where we suppress the dependence of
$E$
[see (2.1)], where we suppress the dependence of
![]() $\widetilde H_0$
and
$\widetilde H_0$
and
![]() $E$
on
$E$
on
![]() $n=m/2$
to simplify the notation. There are two interesting features: first, the singular values of
$n=m/2$
to simplify the notation. There are two interesting features: first, the singular values of
![]() $\widetilde H_0$
may be written out explicitly in terms of the eigenvalues of the Hermitian matrix
$\widetilde H_0$
may be written out explicitly in terms of the eigenvalues of the Hermitian matrix
![]() $A$
(which are well-understood; see Lemma 3.9); and second, the matrix
$A$
(which are well-understood; see Lemma 3.9); and second, the matrix
![]() $E$
is completely determined by the matrix
$E$
is completely determined by the matrix
![]() $\widetilde H_0$
, making this a novel application of the replacement principle (Theorem 3.2 and Corollary 3.3) where the sequence of matrices
$\widetilde H_0$
, making this a novel application of the replacement principle (Theorem 3.2 and Corollary 3.3) where the sequence of matrices
![]() $\widetilde H_0 + E= \widetilde H$
has some dependencies among the entries.
$\widetilde H_0 + E= \widetilde H$
has some dependencies among the entries.
Lemma 3.5.
Assume
![]() $0< p \le p_0<1$
for a constant
$0< p \le p_0<1$
for a constant
![]() $p_0$
. Further assume
$p_0$
. Further assume
![]() $np/\log n\to \infty$
. For
$np/\log n\to \infty$
. For
![]() $E$
as defined in (
2.1
), we have that
$E$
as defined in (
2.1
), we have that
![]() $\|E\|\le 20 \sqrt{\frac{{\log n}}{np}}$
almost surely for all but finitely many
$\|E\|\le 20 \sqrt{\frac{{\log n}}{np}}$
almost surely for all but finitely many
![]() $n$
. In particular,
$n$
. In particular,
![]() $\|E\|$
converges to zero almost surely for all but finitely many
$\|E\|$
converges to zero almost surely for all but finitely many
![]() $n$
.
$n$
.
Proof. First, note that
![]() ${\mathbb E } D= (n-1)p I = (\alpha +1)I$
and thus
${\mathbb E } D= (n-1)p I = (\alpha +1)I$
and thus
 \begin{equation*}E\;:\!=\; \left ( \begin{array}{c@{\quad}c} 0 & I+\frac {1}{\alpha }(I-D) \\[5pt] 0 & 0 \end {array} \right )= \left ( \begin {array}{c@{\quad}c} 0 & \frac {1}{\alpha }({\mathbb E } D-D) \\[5pt] 0 & 0 \end {array} \right ).\end{equation*}
\begin{equation*}E\;:\!=\; \left ( \begin{array}{c@{\quad}c} 0 & I+\frac {1}{\alpha }(I-D) \\[5pt] 0 & 0 \end {array} \right )= \left ( \begin {array}{c@{\quad}c} 0 & \frac {1}{\alpha }({\mathbb E } D-D) \\[5pt] 0 & 0 \end {array} \right ).\end{equation*}
Since
![]() ${\mathbb E } D-D$
is a diagonal matrix, it is easy to check that
${\mathbb E } D-D$
is a diagonal matrix, it is easy to check that
Note that
![]() $D_{ii}$
’s have the same distribution. By the union bound, it follows that for any
$D_{ii}$
’s have the same distribution. By the union bound, it follows that for any
![]() $s>0$
,
$s>0$
,
 \begin{equation*}{\mathbb {P}}(\|E\| \ge s) \le n {\mathbb {P}}\left (\frac {1}{\alpha } |D_{11}- (n-1)p| \ge s \right )=n {\mathbb {P}}\left (\frac {1}{\alpha } \Big |\sum _{j=2}^n a_{1j}- (n-1)p \Big | \ge s \right ).\end{equation*}
\begin{equation*}{\mathbb {P}}(\|E\| \ge s) \le n {\mathbb {P}}\left (\frac {1}{\alpha } |D_{11}- (n-1)p| \ge s \right )=n {\mathbb {P}}\left (\frac {1}{\alpha } \Big |\sum _{j=2}^n a_{1j}- (n-1)p \Big | \ge s \right ).\end{equation*}
Next we will apply the following general form of Chernoff bound.
Theorem 3.6 (Chernoff bound [Reference Chernoff10]). Assume
![]() $\xi _1,\ldots,\xi _n$
are iid random variables and
$\xi _1,\ldots,\xi _n$
are iid random variables and
![]() $\xi _i\in [0,1]$
for all
$\xi _i\in [0,1]$
for all
![]() $i$
. Let
$i$
. Let
![]() $p={\mathbb E } \xi _i$
and
$p={\mathbb E } \xi _i$
and
![]() $S_n = \sum _{i=1}^n \xi _i$
, then for any
$S_n = \sum _{i=1}^n \xi _i$
, then for any
![]() $\varepsilon >0$
,
$\varepsilon >0$
,
 \begin{align*} &{\mathbb{P}}(S_n - np \ge n\varepsilon ) \le \exp \left (-\mbox{RE}(p+\varepsilon || p) n \right );\\[5pt] &{\mathbb{P}}(S_n - np \le -n\varepsilon ) \le \exp \left (-\mbox{RE}(p-\varepsilon || p) n \right ) \end{align*}
\begin{align*} &{\mathbb{P}}(S_n - np \ge n\varepsilon ) \le \exp \left (-\mbox{RE}(p+\varepsilon || p) n \right );\\[5pt] &{\mathbb{P}}(S_n - np \le -n\varepsilon ) \le \exp \left (-\mbox{RE}(p-\varepsilon || p) n \right ) \end{align*}
where
![]() $\mbox{RE}(p||q)= p\log (\frac{p}{q}) + (1-p) \log (\frac{1-p}{1-q})$
is the relative entropy or Kullback-Leibler divergence.
$\mbox{RE}(p||q)= p\log (\frac{p}{q}) + (1-p) \log (\frac{1-p}{1-q})$
is the relative entropy or Kullback-Leibler divergence.
By our assumption,
![]() $np=\omega (n)\log n$
where
$np=\omega (n)\log n$
where
![]() $\omega (n)$
is a positive function that tends to infinity with
$\omega (n)$
is a positive function that tends to infinity with
![]() $n$
. Now take
$n$
. Now take
![]() $K=(n-1)p+npt$
where
$K=(n-1)p+npt$
where
![]() $t=t(n)=10 \sqrt{\frac{\log n}{np}}$
(say). Our assumption
$t=t(n)=10 \sqrt{\frac{\log n}{np}}$
(say). Our assumption
![]() $np/\log n\to \infty$
implies
$np/\log n\to \infty$
implies
![]() $t\to 0$
with
$t\to 0$
with
![]() $n$
. Thus
$n$
. Thus
 \begin{align*}{\mathbb{P}} \left (\sum _{j=2}^n a_{1j} \ge K \right ) ={\mathbb{P}} \left (\sum _{j=2}^n a_{1j} -(n-1)p \ge npt \right ) \le \exp (-\mbox{RE}(p+pt|| p) n) \end{align*}
\begin{align*}{\mathbb{P}} \left (\sum _{j=2}^n a_{1j} \ge K \right ) ={\mathbb{P}} \left (\sum _{j=2}^n a_{1j} -(n-1)p \ge npt \right ) \le \exp (-\mbox{RE}(p+pt|| p) n) \end{align*}
where
 \begin{align*} \mbox{RE}\left (p+pt ||p \right )&= p(1+t)\log (1+t) + (1-p-pt)\log \left (\frac{1-p-pt}{1-p} \right )\\[5pt] &=p(1+t)\log (1+t) - (1-p-pt )\log \left (1+\frac{pt}{1-p-pt} \right )\\[5pt] & > p(1+t)(t-t^2/2) - pt =pt^2(1-t)/2 \end{align*}
\begin{align*} \mbox{RE}\left (p+pt ||p \right )&= p(1+t)\log (1+t) + (1-p-pt)\log \left (\frac{1-p-pt}{1-p} \right )\\[5pt] &=p(1+t)\log (1+t) - (1-p-pt )\log \left (1+\frac{pt}{1-p-pt} \right )\\[5pt] & > p(1+t)(t-t^2/2) - pt =pt^2(1-t)/2 \end{align*}
by the elementary inequalities
![]() $x-x^2/2<\log (1+x)< x$
for
$x-x^2/2<\log (1+x)< x$
for
![]() $x>0$
.
$x>0$
.
Therefore, for
![]() $n$
sufficiently large, taking
$n$
sufficiently large, taking
![]() $t=5 \sqrt{\frac{\log n}{np}}$
, we get
$t=5 \sqrt{\frac{\log n}{np}}$
, we get
 \begin{equation*}{\mathbb {P}} \left (\sum _{j=2}^n a_{1j} \ge (n-1)p+npt \right ) \le \exp \left (-\frac {np t^2(1-t)}{2} \right )\le \exp (-10\log n)= n^{-10}.\end{equation*}
\begin{equation*}{\mathbb {P}} \left (\sum _{j=2}^n a_{1j} \ge (n-1)p+npt \right ) \le \exp \left (-\frac {np t^2(1-t)}{2} \right )\le \exp (-10\log n)= n^{-10}.\end{equation*}
Similarly, take
![]() $L=(n-1)p-npt$
where
$L=(n-1)p-npt$
where
![]() $t=5 \sqrt{\frac{\log n}{np}}$
. Applying the Chernoff bound yields that
$t=5 \sqrt{\frac{\log n}{np}}$
. Applying the Chernoff bound yields that
 \begin{align*}{\mathbb{P}} \left (\sum _{j=2}^n a_{1j} \le L \right ) ={\mathbb{P}} \left (\sum _{j=1}^n a_{1j} -(n-1)p \le -npt \right ) \le \exp \left (-\mbox{RE}(p-pt|| p) n \right ). \end{align*}
\begin{align*}{\mathbb{P}} \left (\sum _{j=2}^n a_{1j} \le L \right ) ={\mathbb{P}} \left (\sum _{j=1}^n a_{1j} -(n-1)p \le -npt \right ) \le \exp \left (-\mbox{RE}(p-pt|| p) n \right ). \end{align*}
We take
![]() $n$
sufficiently large such that
$n$
sufficiently large such that
![]() $t=t(n)<0.01$
(say). Then
$t=t(n)<0.01$
(say). Then
 \begin{align*} \mbox{RE}(p-pt ||p)&= p(1-t)\log (1-t) + (1-p+pt)\log \left (\frac{1-p+pt}{1-p} \right )\\[5pt] &=p(1-t)\log (1-t) - (1-p+pt )\log \left (1-\frac{pt}{1-p+pt} \right )\\[5pt] & > p(1-t)(-t-\frac{3}{5}t^2) + pt = \frac{1}{5}pt^2(2+3t) \ge \frac{2}{5}pt^2 \end{align*}
\begin{align*} \mbox{RE}(p-pt ||p)&= p(1-t)\log (1-t) + (1-p+pt)\log \left (\frac{1-p+pt}{1-p} \right )\\[5pt] &=p(1-t)\log (1-t) - (1-p+pt )\log \left (1-\frac{pt}{1-p+pt} \right )\\[5pt] & > p(1-t)(-t-\frac{3}{5}t^2) + pt = \frac{1}{5}pt^2(2+3t) \ge \frac{2}{5}pt^2 \end{align*}
where we use the fact that
![]() $\log (1-x)<-x$
for
$\log (1-x)<-x$
for
![]() $x\in (0,1)$
and
$x\in (0,1)$
and
![]() $\log (1-x)>-x-\frac{3}{5}x^2$
for
$\log (1-x)>-x-\frac{3}{5}x^2$
for
![]() $x\in (0,0.01)$
. Hence, we get
$x\in (0,0.01)$
. Hence, we get
 \begin{align} {\mathbb{P}}\left (\sum _{j=2}^n a_{1j} \le (n-1)p-npt \right ) \le \exp \left ( - \frac{2}{5}pt^2\right )=\exp (-10\log n) = n^{-10}. \end{align}
\begin{align} {\mathbb{P}}\left (\sum _{j=2}^n a_{1j} \le (n-1)p-npt \right ) \le \exp \left ( - \frac{2}{5}pt^2\right )=\exp (-10\log n) = n^{-10}. \end{align}
Since
![]() $2\alpha t = 2((n-1)p-1) t \ge npt$
for
$2\alpha t = 2((n-1)p-1) t \ge npt$
for
![]() $n$
sufficiently large, it follows that
$n$
sufficiently large, it follows that
 \begin{align*} &{\mathbb{P}}\left (\|E\| \ge 10 \sqrt{\frac{\log n}{np}} \right ) \le n{\mathbb{P}} \left (\left |\sum _{j=2}^n a_{1j}-(n-1)p \right | \ge 2\alpha t \right ) \\[5pt] &\le n{\mathbb{P}}\left (\sum _{j=2}^n a_{1j}\ge (n-1)p + npt \right ) +n{\mathbb{P}}\left (\sum _{j=2}^n a_{1j}\le (n-1)p - npt \right ) \le 2n^{-10}. \end{align*}
\begin{align*} &{\mathbb{P}}\left (\|E\| \ge 10 \sqrt{\frac{\log n}{np}} \right ) \le n{\mathbb{P}} \left (\left |\sum _{j=2}^n a_{1j}-(n-1)p \right | \ge 2\alpha t \right ) \\[5pt] &\le n{\mathbb{P}}\left (\sum _{j=2}^n a_{1j}\ge (n-1)p + npt \right ) +n{\mathbb{P}}\left (\sum _{j=2}^n a_{1j}\le (n-1)p - npt \right ) \le 2n^{-10}. \end{align*}
By the Borel-Cantelli lemma, we have that
![]() $\|E\| \le 10 \sqrt{\frac{\log n}{np}}$
almost surely for all but finitely many
$\|E\| \le 10 \sqrt{\frac{\log n}{np}}$
almost surely for all but finitely many
![]() $n$
.
$n$
.
To show (3.3), we combine Hoeffding’s inequality and Lemma 3.5 to prove the following lemma.
Lemma 3.7.
Assume
![]() $0< p \le p_0<1$
for a constant
$0< p \le p_0<1$
for a constant
![]() $p_0$
. Further assume
$p_0$
. Further assume
![]() $np/\log n\to \infty$
. For
$np/\log n\to \infty$
. For
![]() $\widetilde H_0$
and
$\widetilde H_0$
and
![]() $E$
as defined in (
2.1
), we have that both
$E$
as defined in (
2.1
), we have that both
![]() $\frac{1}{2n} \|\widetilde H_0\|_F^2$
and
$\frac{1}{2n} \|\widetilde H_0\|_F^2$
and
![]() $\frac{1}{2n} \|\widetilde H_0+E\|_F^2$
are almost surely bounded.
$\frac{1}{2n} \|\widetilde H_0+E\|_F^2$
are almost surely bounded.
Proof. We begin by stating Hoeffding’s inequality [Reference Hoeffding20].
Theorem 3.8 (Hoeffding’s inequality [Reference Hoeffding20]). Let
![]() $\beta _1,\ldots,\beta _k$
be independent random variables such that for
$\beta _1,\ldots,\beta _k$
be independent random variables such that for
![]() $1\le i \le k$
we have
$1\le i \le k$
we have
![]() ${\mathbb{P}}(\beta _i \in [a_i,b_i]) = 1.$
Let
${\mathbb{P}}(\beta _i \in [a_i,b_i]) = 1.$
Let
![]() $S\;:\!=\; \sum _{i=1}^k \beta _i$
. Then for any real
$S\;:\!=\; \sum _{i=1}^k \beta _i$
. Then for any real
![]() $t$
,
$t$
,
 \begin{equation*}{\mathbb {P}}(\left \lvert {S- {\mathbb E }(S) }\right \rvert \ge kt ) \le 2\exp \left ( - \frac {2 k^2 t^2}{\sum _{i=1}^k (b_i -a_i)^2}\right ).\end{equation*}
\begin{equation*}{\mathbb {P}}(\left \lvert {S- {\mathbb E }(S) }\right \rvert \ge kt ) \le 2\exp \left ( - \frac {2 k^2 t^2}{\sum _{i=1}^k (b_i -a_i)^2}\right ).\end{equation*}
Recall that
![]() $\alpha =(n-1)p-1$
and
$\alpha =(n-1)p-1$
and
 $\widetilde H_0= \left ( \begin{matrix} \frac{1}{\sqrt{\alpha }} A & -I \\[5pt] I & 0 \end{matrix} \right )$
, where
$\widetilde H_0= \left ( \begin{matrix} \frac{1}{\sqrt{\alpha }} A & -I \\[5pt] I & 0 \end{matrix} \right )$
, where
![]() $A=(a_{ij})_{1\le i, j \le n}$
is the adjacency matrix of an Erdős-Rényi random graph
$A=(a_{ij})_{1\le i, j \le n}$
is the adjacency matrix of an Erdős-Rényi random graph
![]() $G(n,p)$
. Thus
$G(n,p)$
. Thus
To apply Hoeffding’s inequality, note that
![]() $a_{ij}$
$a_{ij}$
![]() $(i<j)$
are iid random variables each taking the value 1 with probability
$(i<j)$
are iid random variables each taking the value 1 with probability
![]() $p$
and 0 otherwise. Let
$p$
and 0 otherwise. Let
![]() $b_i=1$
and
$b_i=1$
and
![]() $a_i=0$
for all
$a_i=0$
for all
![]() $i$
, and let
$i$
, and let
![]() $k=\left(\substack{n\\[2pt] 2}\right)$
, which is the number of random entries in
$k=\left(\substack{n\\[2pt] 2}\right)$
, which is the number of random entries in
![]() $A$
(recall that the diagonal of
$A$
(recall that the diagonal of
![]() $A$
is all zeros by assumption). Letting
$A$
is all zeros by assumption). Letting
![]() $S=\sum _{i<j} a_{ij}$
, we see that
$S=\sum _{i<j} a_{ij}$
, we see that
![]() $\mathbb E S = kp$
and so
$\mathbb E S = kp$
and so
Since
![]() $\|\widetilde H_0\|_F^2 = \frac{2}{\alpha } S + 2n$
, we obtain that
$\|\widetilde H_0\|_F^2 = \frac{2}{\alpha } S + 2n$
, we obtain that
Take
![]() $t=p$
. For
$t=p$
. For
![]() $n$
sufficiently large,
$n$
sufficiently large,
and since
![]() $p\ge \omega (n) \log n/n$
for
$p\ge \omega (n) \log n/n$
for
![]() $\omega (n)>0$
and
$\omega (n)>0$
and
![]() $\omega (n)\to \infty$
with
$\omega (n)\to \infty$
with
![]() $n$
, we get
$n$
, we get
By the Borel-Cantelli lemma, we conclude that
![]() $\frac{1}{2n}\|\tilde{H}_0\|_F^2$
is bounded almost surely. Since
$\frac{1}{2n}\|\tilde{H}_0\|_F^2$
is bounded almost surely. Since
![]() $\|E\|_{\max }=\|E\|$
, by triangle inequality, we see
$\|E\|_{\max }=\|E\|$
, by triangle inequality, we see
 \begin{align*} \frac{1}{2n} \|\widetilde H_0+E\|_F^2 &\le \frac{1}{2n} (\|\tilde{H}_0\|_F + \|E\|_F)^2\le \frac{1}{n} \|\tilde{H}_0\|_F^2 + \frac{1}{n} \|E\|_F^2 \\[5pt] &\le \frac{1}{n} \|\tilde{H}_0\|_F^2 + \|E\|. \end{align*}
\begin{align*} \frac{1}{2n} \|\widetilde H_0+E\|_F^2 &\le \frac{1}{2n} (\|\tilde{H}_0\|_F + \|E\|_F)^2\le \frac{1}{n} \|\tilde{H}_0\|_F^2 + \frac{1}{n} \|E\|_F^2 \\[5pt] &\le \frac{1}{n} \|\tilde{H}_0\|_F^2 + \|E\|. \end{align*}
By Lemma 3.5, we get
![]() $\frac{1}{2n} \|\widetilde H_0+E\|_F^2$
is bounded almost surely. This completes the proof.
$\frac{1}{2n} \|\widetilde H_0+E\|_F^2$
is bounded almost surely. This completes the proof.
The last part of proving Theorem 3.1 by way of Corollary 3.3 is proving that (3.5) holds with
![]() $M_m=\widetilde H_0$
and
$M_m=\widetilde H_0$
and
![]() $f(z,m)=C_z$
, a constant depending only on
$f(z,m)=C_z$
, a constant depending only on
![]() $z$
, as given below in Lemma 3.9. Note that (3.4) follows by combining Lemma 3.5 and Lemma 3.9. The following lemma will be proved by writing a formula for the singular values of
$z$
, as given below in Lemma 3.9. Note that (3.4) follows by combining Lemma 3.5 and Lemma 3.9. The following lemma will be proved by writing a formula for the singular values of
![]() $\widetilde H_0$
in terms of the eigenvalues of the adjacency matrix
$\widetilde H_0$
in terms of the eigenvalues of the adjacency matrix
![]() $A$
, which are well-understood. A number of elementary technical details will be needed to prove that the smallest singular value is bounded away from zero, and these appear in Lemma 3.10.
$A$
, which are well-understood. A number of elementary technical details will be needed to prove that the smallest singular value is bounded away from zero, and these appear in Lemma 3.10.
Lemma 3.9.
Let
![]() $\widetilde H_0$
be as defined in (
2.1
) and let
$\widetilde H_0$
be as defined in (
2.1
) and let
![]() $z$
be a complex number such that
$z$
be a complex number such that
![]() ${\mathsf{Im}}(z) \ne 0$
and
${\mathsf{Im}}(z) \ne 0$
and
![]() $\left \lvert{z}\right \rvert \ne 1$
(note that these conditions exclude a set of complex numbers of Lebesgue measure zero). Then there exists a constant
$\left \lvert{z}\right \rvert \ne 1$
(note that these conditions exclude a set of complex numbers of Lebesgue measure zero). Then there exists a constant
![]() $C_z$
depending only on
$C_z$
depending only on
![]() $z$
such that
$z$
such that
![]() $\left \|{ (\widetilde H_0 -zI)^{-1}}\right \| \le C_z$
with probability 1 for all but finitely many
$\left \|{ (\widetilde H_0 -zI)^{-1}}\right \| \le C_z$
with probability 1 for all but finitely many
![]() $n$
.
$n$
.
Proof. We will compute all the singular values of
![]() $\widetilde H_0 -zI$
, showing that they are bounded away from zero by a constant depending on
$\widetilde H_0 -zI$
, showing that they are bounded away from zero by a constant depending on
![]() $z$
. The proof does not use randomness and depends only on facts about the determinant and singular values and on the structure of
$z$
. The proof does not use randomness and depends only on facts about the determinant and singular values and on the structure of
![]() $\widetilde H_0$
; in fact, the proof is the same if
$\widetilde H_0$
; in fact, the proof is the same if
![]() $\widetilde H_0$
is replaced with any matrix
$\widetilde H_0$
is replaced with any matrix
 $\begin{pmatrix} M& -I \\[5pt] I & 0 \end{pmatrix}$
with
$\begin{pmatrix} M& -I \\[5pt] I & 0 \end{pmatrix}$
with
![]() $M$
Hermitian.
$M$
Hermitian.
To find the singular values of
![]() $\widetilde H_0$
we will compute the characteristic polynomial
$\widetilde H_0$
we will compute the characteristic polynomial
![]() $\chi (\tilde w)$
for
$\chi (\tilde w)$
for
![]() $(\widetilde H_0 -zI)(\widetilde H_0 -zI)^*$
, using the definition of
$(\widetilde H_0 -zI)(\widetilde H_0 -zI)^*$
, using the definition of
![]() $\widetilde H_0$
in (2.1), and assuming that
$\widetilde H_0$
in (2.1), and assuming that
![]() $\tilde w= w + 1+{\left \lvert{z}\right \rvert }^2$
; thus,
$\tilde w= w + 1+{\left \lvert{z}\right \rvert }^2$
; thus,
 \begin{eqnarray*} \chi (\tilde w)&\;:\!=\;\det \left ((\widetilde H_0 -zI)(\widetilde H_0 -zI)^* - (w+1+\left \lvert{z}\right \rvert ^2)I\right ) \\[5pt] &=\det \begin{pmatrix} \frac{A^2}{\alpha } - (z+\bar z) \frac{A}{\sqrt{\alpha }} - wI\;\;\;\;\;\; & \frac{A}{\sqrt{\alpha }} +(\bar z -z) I\\[5pt] \frac{A}{\sqrt{\alpha }} + (z - \bar z)I & -wI \end{pmatrix}. \end{eqnarray*}
\begin{eqnarray*} \chi (\tilde w)&\;:\!=\;\det \left ((\widetilde H_0 -zI)(\widetilde H_0 -zI)^* - (w+1+\left \lvert{z}\right \rvert ^2)I\right ) \\[5pt] &=\det \begin{pmatrix} \frac{A^2}{\alpha } - (z+\bar z) \frac{A}{\sqrt{\alpha }} - wI\;\;\;\;\;\; & \frac{A}{\sqrt{\alpha }} +(\bar z -z) I\\[5pt] \frac{A}{\sqrt{\alpha }} + (z - \bar z)I & -wI \end{pmatrix}. \end{eqnarray*}
We can use the fact that if
 $\begin{pmatrix}X & Y \\[5pt] Z & W\end{pmatrix}$
is a matrix composed of four
$\begin{pmatrix}X & Y \\[5pt] Z & W\end{pmatrix}$
is a matrix composed of four
![]() $n\times n$
square blocks where
$n\times n$
square blocks where
![]() $W$
and
$W$
and
![]() $Z$
commute, then
$Z$
commute, then
 $\det \begin{pmatrix}X & Y \\[5pt] Z & W\end{pmatrix} = \det (XW-YZ)$
(see [Reference Silvester33, Theorem 3]). Thus, it is equivalent to consider
$\det \begin{pmatrix}X & Y \\[5pt] Z & W\end{pmatrix} = \det (XW-YZ)$
(see [Reference Silvester33, Theorem 3]). Thus, it is equivalent to consider
Because
![]() $\frac{A}{\sqrt{\alpha }}$
is Hermitian, it can be diagonalized to
$\frac{A}{\sqrt{\alpha }}$
is Hermitian, it can be diagonalized to
![]() $L={\textrm{diag}}(\lambda _1,\ldots,\lambda _n)$
, and thus the above determinant becomes:
$L={\textrm{diag}}(\lambda _1,\ldots,\lambda _n)$
, and thus the above determinant becomes:
 \begin{align*} &\det \left ( w\left (\frac{A^2}{\alpha } - (z+\bar z) \frac{A}{\sqrt{\alpha }} -w I\right ) + \left (\frac{A}{\sqrt{\alpha }} +(\bar z -z) I\right )\left (\frac{A}{\sqrt{\alpha }} + (z - \bar z)I\right ) \right )\\[5pt] &\quad = \det \left ( w\left (L^2 - (z+\bar z) L -w I\right ) + \left (L +(\bar z -z) I\right )\left ( L + (z - \bar z)I\right ) \right )\\[5pt] &\quad = \prod _{i=1}^n \left (w \left (\lambda _i^2 - (z+\bar z) \lambda _i -w \right )+ \left ( \lambda _i + (z - \bar z)\right )\left (\lambda _i +(\bar z -z) \right ) \right )\\[5pt] &\quad = \prod _{i=1}^n \left ( -w^2 + w\left ( \lambda _i^2 - (z+\bar z) \lambda _i \right ) + \lambda _i^2-(z-\bar z)^2 \right ). \end{align*}
\begin{align*} &\det \left ( w\left (\frac{A^2}{\alpha } - (z+\bar z) \frac{A}{\sqrt{\alpha }} -w I\right ) + \left (\frac{A}{\sqrt{\alpha }} +(\bar z -z) I\right )\left (\frac{A}{\sqrt{\alpha }} + (z - \bar z)I\right ) \right )\\[5pt] &\quad = \det \left ( w\left (L^2 - (z+\bar z) L -w I\right ) + \left (L +(\bar z -z) I\right )\left ( L + (z - \bar z)I\right ) \right )\\[5pt] &\quad = \prod _{i=1}^n \left (w \left (\lambda _i^2 - (z+\bar z) \lambda _i -w \right )+ \left ( \lambda _i + (z - \bar z)\right )\left (\lambda _i +(\bar z -z) \right ) \right )\\[5pt] &\quad = \prod _{i=1}^n \left ( -w^2 + w\left ( \lambda _i^2 - (z+\bar z) \lambda _i \right ) + \lambda _i^2-(z-\bar z)^2 \right ). \end{align*}
The quadratic factors can then be explicitly factored, showing that each
![]() $\lambda _i$
generates two singular values for
$\lambda _i$
generates two singular values for
![]() $\widetilde H_0 -zI$
, each being the positive square root of
$\widetilde H_0 -zI$
, each being the positive square root of
The proof of Lemma 3.9 is thus completed by Lemma 3.10 (stated and proved below), which shows that the quantity above is bounded from below by a positive constant depending only on
![]() $z$
.
$z$
.
Lemma 3.10.
Let
![]() $z$
be a complex number satisfying
$z$
be a complex number satisfying
![]() ${\mathsf{Im}}(z) \ne 0$
and
${\mathsf{Im}}(z) \ne 0$
and
![]() $\left \lvert{z}\right \rvert \ne 1$
. Then for any real number
$\left \lvert{z}\right \rvert \ne 1$
. Then for any real number
![]() $\lambda$
, we have that
$\lambda$
, we have that
where
![]() $C_z$
is a positive real constant depending only on
$C_z$
is a positive real constant depending only on
![]() $z$
.
$z$
.
The proof of Lemma 3.10 is given in the appendixFootnote 1 using elementary calculus, facts about matrices, and case analysis. Lemma 3.10 completes the proof of Lemma 3.5 and thus of Theorem 3.1.
4. Perturbation theory: proving Theorem 1.6
In this section, we study the eigenvalues of
![]() $H$
via perturbation theory. Recall from that the discussion in the beginning of Section 2 that
$H$
via perturbation theory. Recall from that the discussion in the beginning of Section 2 that
![]() $\widetilde H$
in (2.1) has the same eigenvalues as
$\widetilde H$
in (2.1) has the same eigenvalues as
![]() $H/\sqrt{\alpha }$
. We consider
$H/\sqrt{\alpha }$
. We consider
![]() $\widetilde H = \widetilde H_0 + E$
where
$\widetilde H = \widetilde H_0 + E$
where
 $E= \left ( \begin{array}{c@{\quad}c} 0 & I+\frac{1}{\alpha }(I-D) \\[5pt] 0 & 0 \end{array} \right )\!.$
Note that
$E= \left ( \begin{array}{c@{\quad}c} 0 & I+\frac{1}{\alpha }(I-D) \\[5pt] 0 & 0 \end{array} \right )\!.$
Note that
![]() $H_0/\sqrt{\alpha }$
and
$H_0/\sqrt{\alpha }$
and
![]() $\widetilde H_0$
also have identical eigenvalues.
$\widetilde H_0$
also have identical eigenvalues.
Let us begin by defining the spectral separation of matrices. Denote the eigenvalues of a matrix
![]() $M$
by
$M$
by
![]() $\eta _i(M)$
’s. The spectral variation of
$\eta _i(M)$
’s. The spectral variation of
![]() $M+E$
with respect to
$M+E$
with respect to
![]() $M$
is defined by
$M$
is defined by
Theorem 4.1 (Bauer-Fike theorem; see Theorem 6 from [Reference Bordenave, Lelarge and Massoulié8]). If
![]() $H_0$
is diagonalizable by the matrix
$H_0$
is diagonalizable by the matrix
![]() $Y$
, then
$Y$
, then
Denote by
![]() $\mathcal{C}_i\;:\!=\;\mathcal{B}(\mu _i(H_0), R)$
the ball in
$\mathcal{C}_i\;:\!=\;\mathcal{B}(\mu _i(H_0), R)$
the ball in
![]() $\mathbb{C}$
centred at
$\mathbb{C}$
centred at
![]() $\mu _i(H_0)$
with radius
$\mu _i(H_0)$
with radius
![]() $R=\left \|{E}\right \| \cdot \left \|{Y}\right \| \cdot \|Y^{-1}\|$
. Let
$R=\left \|{E}\right \| \cdot \left \|{Y}\right \| \cdot \|Y^{-1}\|$
. Let
![]() $\mathcal{I}$
be a set of indices such that
$\mathcal{I}$
be a set of indices such that
Then the number of eigenvalues of
![]() $H_0 + E$
in
$H_0 + E$
in
![]() $\cup _{i\in \mathcal{I}} \mathcal{C}_i$
is exactly
$\cup _{i\in \mathcal{I}} \mathcal{C}_i$
is exactly
![]() $|\mathcal{I}|$
.
$|\mathcal{I}|$
.
We will bound the operator norm of
![]() $E$
and the condition number
$E$
and the condition number
![]() $\left \|{Y}\right \| \left \|{Y^{-1}}\right \|$
of
$\left \|{Y}\right \| \left \|{Y^{-1}}\right \|$
of
![]() $Y$
to prove Theorem 1.6.
$Y$
to prove Theorem 1.6.
By Lemma 3.5, we know that
![]() $\left \|{E}\right \| \le 20\sqrt{\frac{\log n}{np}}$
with probability 1 for all but finitely many
$\left \|{E}\right \| \le 20\sqrt{\frac{\log n}{np}}$
with probability 1 for all but finitely many
![]() $n$
.
$n$
.
To bound the condition number of
![]() $Y$
, we note that the square of the condition number of
$Y$
, we note that the square of the condition number of
![]() $Y$
is equal to the largest eigenvalue of
$Y$
is equal to the largest eigenvalue of
![]() $YY^*$
divided by the smallest eigenvalue of
$YY^*$
divided by the smallest eigenvalue of
![]() $YY^*$
. Using the explicit definition of
$YY^*$
. Using the explicit definition of
![]() $Y$
from (2.6), we see from the fact that the
$Y$
from (2.6), we see from the fact that the
![]() $v_i$
are orthonormal that
$v_i$
are orthonormal that
where
![]() $Y_i$
’s are
$Y_i$
’s are
![]() $2\times 2$
block matrices of the following form
$2\times 2$
block matrices of the following form
 \begin{equation*} Y_i=\begin {pmatrix} y_{2i-1}^* y_{2i-1} & y_{2i-1}^* y_{2i}\\[5pt] y_{2i}^* y_{2i-1} & y_{2i}^* y_{2i} \end {pmatrix}. \end{equation*}
\begin{equation*} Y_i=\begin {pmatrix} y_{2i-1}^* y_{2i-1} & y_{2i-1}^* y_{2i}\\[5pt] y_{2i}^* y_{2i-1} & y_{2i}^* y_{2i} \end {pmatrix}. \end{equation*}
Recall that
We then have
 $ Y_i=\begin{pmatrix} 1 & \gamma _i\\[5pt] \overline{\gamma }_i & 1 \end{pmatrix}$
where
$ Y_i=\begin{pmatrix} 1 & \gamma _i\\[5pt] \overline{\gamma }_i & 1 \end{pmatrix}$
where
It is easy to check that the eigenvalues of
![]() $Y_i$
are
$Y_i$
are
![]() $1\pm |\gamma _i|$
. The eigenvalues of
$1\pm |\gamma _i|$
. The eigenvalues of
![]() $YY^*$
are the union of all the eigenvalues of the blocks, and so we will compute the eigenvalues
$YY^*$
are the union of all the eigenvalues of the blocks, and so we will compute the eigenvalues
![]() $1\pm |\gamma _i|$
based on whether
$1\pm |\gamma _i|$
based on whether
![]() $\lambda _i$
produced real or complex eigenvalues for
$\lambda _i$
produced real or complex eigenvalues for
![]() $\widetilde H_0$
.
$\widetilde H_0$
.
For
![]() $i=1$
, the eigenvalue
$i=1$
, the eigenvalue
![]() $\lambda _1$
produces two real eigenvalues for
$\lambda _1$
produces two real eigenvalues for
![]() $\widetilde H_0$
. Using the facts that
$\widetilde H_0$
. Using the facts that
![]() $\mu _{1}\mu _{2}=1$
and
$\mu _{1}\mu _{2}=1$
and
![]() $\mu _{1}+ \mu _{2}=\lambda _1$
, which together imply that
$\mu _{1}+ \mu _{2}=\lambda _1$
, which together imply that
![]() $\mu _{1}^2+\mu _{2}^2 = \lambda _1^2-2$
, we see that in this case
$\mu _{1}^2+\mu _{2}^2 = \lambda _1^2-2$
, we see that in this case
![]() $\gamma _1^2=\frac{4}{\lambda _1^2}$
, and so the two eigenvalues corresponding to this block are
$\gamma _1^2=\frac{4}{\lambda _1^2}$
, and so the two eigenvalues corresponding to this block are
![]() $1\pm |\gamma _1|=1 \pm 2/\left \lvert{\lambda _1}\right \rvert$
. By (2.4), we see that
$1\pm |\gamma _1|=1 \pm 2/\left \lvert{\lambda _1}\right \rvert$
. By (2.4), we see that
![]() $1\pm |\gamma _i| = 1\pm \frac{2}{\sqrt{np}}(1+o(1))$
with probability
$1\pm |\gamma _i| = 1\pm \frac{2}{\sqrt{np}}(1+o(1))$
with probability
![]() $1-o(1)$
.
$1-o(1)$
.
For
![]() $i\ge 2$
, the eigenvalue
$i\ge 2$
, the eigenvalue
![]() $\lambda _i$
produces two complex eigenvalues for
$\lambda _i$
produces two complex eigenvalues for
![]() $\widetilde H_0$
, both with absolute value 1 (see Section 2). In this case,
$\widetilde H_0$
, both with absolute value 1 (see Section 2). In this case,
![]() $\gamma _i = \frac{1+\mu _{2i-1}^2}{2}$
. Again using the facts that
$\gamma _i = \frac{1+\mu _{2i-1}^2}{2}$
. Again using the facts that
![]() $\mu _{2i-1}\mu _{2i}=1$
and
$\mu _{2i-1}\mu _{2i}=1$
and
![]() $\mu _{2i-1}^2+\mu _{2i}^2 = \lambda _i^2-2$
, we see that
$\mu _{2i-1}^2+\mu _{2i}^2 = \lambda _i^2-2$
, we see that
![]() $\overline \gamma _i \gamma _i = \lambda _i^2/4$
, which shows that the two eigenvalues corresponding to this block are
$\overline \gamma _i \gamma _i = \lambda _i^2/4$
, which shows that the two eigenvalues corresponding to this block are
![]() $1 \pm \left \lvert{\lambda _i}\right \rvert/{2}$
.
$1 \pm \left \lvert{\lambda _i}\right \rvert/{2}$
.
By [Reference Vu36] (see Theorem 2.1 in Section 2) we know that when
![]() $p\ge \frac{\log ^{2/3+\varepsilon } n}{n^{1/6}}$
,
$p\ge \frac{\log ^{2/3+\varepsilon } n}{n^{1/6}}$
,
![]() $\max _{2\le i\le n} \left \lvert{\lambda _i}\right \rvert \le 2 \sqrt{1-p} + O(n^{1/4}\log n/\sqrt{np})$
with probability tending to 1, and thus the largest and smallest eigenvalues coming from any of the blocks corresponding to
$\max _{2\le i\le n} \left \lvert{\lambda _i}\right \rvert \le 2 \sqrt{1-p} + O(n^{1/4}\log n/\sqrt{np})$
with probability tending to 1, and thus the largest and smallest eigenvalues coming from any of the blocks corresponding to
![]() $i\ge 2$
are
$i\ge 2$
are
![]() $1 + \sqrt{1-p} +O(n^{1/4}\log n/\sqrt{np})$
and
$1 + \sqrt{1-p} +O(n^{1/4}\log n/\sqrt{np})$
and
![]() $1-\sqrt{1-p}+ O(n^{1/4}\log n/\sqrt{np})$
with probability tending to 1. Combining this information with the previous paragraph, we see that the condition number for
$1-\sqrt{1-p}+ O(n^{1/4}\log n/\sqrt{np})$
with probability tending to 1. Combining this information with the previous paragraph, we see that the condition number for
![]() $Y$
is
$Y$
is
 \begin{align*} &\sqrt{\frac{1+\sqrt{1-p}+O(n^{1/4}\log n/\sqrt{np})}{1-\sqrt{1-p}+O(n^{1/4}\log n/\sqrt{np})}}=\sqrt{\frac{(1+\sqrt{1-p})^2 + O(n^{-1/4}p^{-1/2}\log n)}{p+ O(n^{-1/4}p^{-1/2}\log n)}}\\[5pt] &=\sqrt{\frac{2}{p} \frac{1+\sqrt{1-p} -p/2 +O(n^{-1/4}p^{-1/2}\log n)}{1+O(n^{-1/4}p^{-3/2}\log n)}} \\[5pt] & = \sqrt{\frac{2}{p} \left ( (1+\sqrt{1-p}) + O(n^{-1/4}p^{-3/2}\log n) \right )} \le \frac{2}{\sqrt{p}} \end{align*}
\begin{align*} &\sqrt{\frac{1+\sqrt{1-p}+O(n^{1/4}\log n/\sqrt{np})}{1-\sqrt{1-p}+O(n^{1/4}\log n/\sqrt{np})}}=\sqrt{\frac{(1+\sqrt{1-p})^2 + O(n^{-1/4}p^{-1/2}\log n)}{p+ O(n^{-1/4}p^{-1/2}\log n)}}\\[5pt] &=\sqrt{\frac{2}{p} \frac{1+\sqrt{1-p} -p/2 +O(n^{-1/4}p^{-1/2}\log n)}{1+O(n^{-1/4}p^{-3/2}\log n)}} \\[5pt] & = \sqrt{\frac{2}{p} \left ( (1+\sqrt{1-p}) + O(n^{-1/4}p^{-3/2}\log n) \right )} \le \frac{2}{\sqrt{p}} \end{align*}
for
![]() $n$
sufficiently large. In the third equation above, we use the Taylor expansion. In the last inequality, we use that
$n$
sufficiently large. In the third equation above, we use the Taylor expansion. In the last inequality, we use that
![]() $n^{-1/4}p^{-3/2}\log n \le \log ^{-3\varepsilon/2} n=o(1)$
since
$n^{-1/4}p^{-3/2}\log n \le \log ^{-3\varepsilon/2} n=o(1)$
since
![]() $p\ge \frac{\log ^{2/3+\varepsilon } n}{n^{1/6}}$
.
$p\ge \frac{\log ^{2/3+\varepsilon } n}{n^{1/6}}$
.
Finally, we apply Lemma 3.5 and Bauer-Fike Theorem (Theorem 4.1) with
![]() $R=\frac{40}{\sqrt{p}}\sqrt{\frac{\log n}{np}}=40\sqrt{\frac{\log n}{np^2}}$
to complete the proof.
$R=\frac{40}{\sqrt{p}}\sqrt{\frac{\log n}{np}}=40\sqrt{\frac{\log n}{np^2}}$
to complete the proof.
Acknowledgements
The first author would like to thank Zhigang Bao for useful discussions. The authors would like to thank the anonymous referees for their valuable suggestions that have enhanced the readability of this paper.