1 results
A posteriori error estimates for a nonconforming finite elementdiscretization of the heat equation
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 2 / March 2005
- Published online by Cambridge University Press:
- 15 April 2005, pp. 319-348
- Print publication:
- March 2005
-
- Article
- Export citation
-
The paper presents an a posteriori error estimator for a (piecewise linear) nonconforming finite element approximation of the heat equationin $\mathbb{R}^d$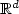
, d=2 or 3,using backward Euler's scheme. For this discretization, we derive a residual indicator, which usea spatial residual indicator based on thejumps of normal and tangential derivatives of the nonconformingapproximation and a time residual indicator based on the jump of broken gradients at each time step.Lower and upper bounds form the main results with minimal assumptions on the mesh.Numerical experiments and a space-time adaptive algorithm confirm the theoretical predictions.
