We give a family of real quadratic fields such that the 2-class field towers over their cyclotomic 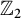 $\mathbb Z_2$
-extensions have metabelian Galois groups of abelian invariants
$\mathbb Z_2$
-extensions have metabelian Galois groups of abelian invariants 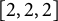 $[2,2,2]$
. We also consider the boundedness of the Galois groups in relation to Greenberg’s conjecture, and calculate their class-2 quotients with an explicit example.
$[2,2,2]$
. We also consider the boundedness of the Galois groups in relation to Greenberg’s conjecture, and calculate their class-2 quotients with an explicit example.
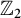 $\mathbb Z_2$
-extensions of real quadratic fields
$\mathbb Z_2$
-extensions of real quadratic fields