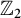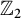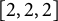Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chems-Eddin, Mohamed Mahmoud
2026.
Greenberg's conjecture and Iwasawa module of real biquadratic fields I.
Journal of Number Theory,
Vol. 281,
Issue. ,
p.
224.