We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In 1971, Griffiths used a generating function to define polynomials in d variables orthogonal with respect to the multinomial distribution. The polynomials possess a duality between the discrete variables and the degree indices. In 2004, Mizukawa and Tanaka related these polynomials to character algebras and the Gelfand hypergeometric series. Using this approach, they clarified the duality and obtained a new proof of the orthogonality. In the present paper, we interpret these polynomials within the context of the Lie algebra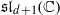 
. Our approach yields yet another proof of the orthogonality. It also shows that the polynomials satisfy d independent recurrence relations each involving d2+d+1 terms. This, combined with the duality, establishes their bispectrality. We illustrate our results with several explicit examples.
