In providing a good foundation for mathematics, set theorists often aim to develop the strongest theories possible and avoid those theories that place undue restrictions on the capacity to possess strength. For example, adding a measurable cardinal to 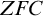$ZFC$ is thought to give a stronger theory than adding $V=L$ and the latter is thought to be more restrictive than the former. The two main proponents of this style of account are Penelope Maddy and John Steel. In this paper, I’ll offer a third account that is intended to provide a simple analysis of restrictiveness based on the algebraic concept of retraction in the category of theories. I will also deliver some results and arguments that suggest some plausible alternative approaches to analyzing restrictiveness do not live up to their intuitive motivation.

This paper critically examines two arguments against the generic multiverse, both of which are due to W. Hugh Woodin. Versions of the first argument have appeared a number of times in print, while the second argument is relatively novel. We shall investigate these arguments through the lens of two different attitudes one may take toward the methodology and metaphysics of set theory; and we shall observe that the impact of these arguments depends significantly on which of these attitudes is upheld. Our examination of the second argument involves the development of a new (inner) model for Steel’s multiverse theory, which is delivered in the Appendix.