We derive a sufficient condition for the linear stability of plasma equilibria with incompressible flow parallel to the magnetic field, 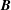 $\boldsymbol{B}$, constant mass density and anisotropic pressure such that the quantity
$\boldsymbol{B}$, constant mass density and anisotropic pressure such that the quantity 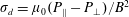 $\unicode[STIX]{x1D70E}_{d}=\unicode[STIX]{x1D707}_{0}(P_{\Vert }-P_{\bot })/B^{2}$, where
$\unicode[STIX]{x1D70E}_{d}=\unicode[STIX]{x1D707}_{0}(P_{\Vert }-P_{\bot })/B^{2}$, where 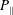 $P_{\Vert }$ (
$P_{\Vert }$ (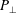 $P_{\bot }$) is the pressure tensor element parallel (perpendicular) to
$P_{\bot }$) is the pressure tensor element parallel (perpendicular) to 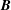 $\boldsymbol{B}$, remains constant. This condition is applicable to any steady state without geometrical restriction. The condition, generalising the respective condition for magnetohydrodynamic equilibria with isotropic pressure and constant density derived in Throumoulopoulos & Tasso (Phys. Plasmas, vol. 14, 2007, 122104), involves physically interpretable terms related to the magnetic shear, the flow shear and the variation of total pressure perpendicular to the magnetic surfaces. On the basis of this condition we prove that, if a given equilibrium is linearly stable, then the ones resulting from the application of Bogoyavlenskij symmetry transformations are linearly stable too, provided that a parameter involved in those transformations is positive. In addition, we examine the impact of pressure anisotropy, flow and torsion of a helical magnetic axis, for a specific class of analytic equilibria. In this case, we find that the pressure anisotropy and the flow may have either stabilising or destabilising effects. Also, helical configurations with small torsion and large pitch seem to have more favourable stability properties.
$\boldsymbol{B}$, remains constant. This condition is applicable to any steady state without geometrical restriction. The condition, generalising the respective condition for magnetohydrodynamic equilibria with isotropic pressure and constant density derived in Throumoulopoulos & Tasso (Phys. Plasmas, vol. 14, 2007, 122104), involves physically interpretable terms related to the magnetic shear, the flow shear and the variation of total pressure perpendicular to the magnetic surfaces. On the basis of this condition we prove that, if a given equilibrium is linearly stable, then the ones resulting from the application of Bogoyavlenskij symmetry transformations are linearly stable too, provided that a parameter involved in those transformations is positive. In addition, we examine the impact of pressure anisotropy, flow and torsion of a helical magnetic axis, for a specific class of analytic equilibria. In this case, we find that the pressure anisotropy and the flow may have either stabilising or destabilising effects. Also, helical configurations with small torsion and large pitch seem to have more favourable stability properties.