Recent work of Ein–Lazarsfeld–Smith and Hochster–Huneke raised the problem of which symbolic powers of an ideal are contained in a given ordinary power of the ideal. Bocci–Harbourne developed methods to address this problem, which involve asymptotic numerical characters of symbolic powers of the ideals. Most of the work done up to now has been done for ideals defining 0-dimensional subschemes of projective space. Here we focus on certain subschemes given by a union of lines in ${{\mathbb{P}}^{3}}$ that can also be viewed as points in ${{\mathbb{P}}^{1}}\times {{\mathbb{P}}^{1}}$. We also obtain results on the closely related problem, studied by Hochster and by Li and Swanson, of determining situations for which each symbolic power of an ideal is an ordinary power.

We study the Hilbert functions of fat points in 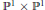${{\mathbb{P}}^{1\,}}\times \,{{\mathbb{P}}^{1}}$. If 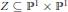$Z\,\subseteq \,{{\mathbb{P}}^{1\,}}\times \,{{\mathbb{P}}^{1}}$ is an arbitrary fat point scheme, then it can be shown that for every 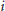$i$ and 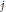$j$ the values of the Hilbert function 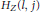${{H}_{Z}}(l,\,j)$ and 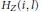${{H}_{Z}}(i,\,l)$ eventually become constant for 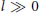$l\,\gg \,0$. We show how to determine these eventual values by using only the multiplicities of the points, and the relative positions of the points in 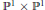${{\mathbb{P}}^{1\,}}\times \,{{\mathbb{P}}^{1}}$. This enables us to compute all but a finite number values of 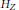${{H}_{Z}}$ without using the coordinates of points. We also characterize the 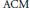$\text{ACM}$ fat point schemes using our description of the eventual behaviour. In fact, in the case that 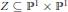$Z\,\subseteq \,{{\mathbb{P}}^{1\,}}\times \,{{\mathbb{P}}^{1}}$ is 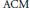$\text{ACM}$, then the entire Hilbert function and its minimal free resolution depend solely on knowing the eventual values of the Hilbert function.