Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Van Tuyl, Adam
2003.
The Hilbert functions of ACM sets of points in Pn1×⋯×Pnk.
Journal of Algebra,
Vol. 264,
Issue. 2,
p.
420.
Guardo, Elena
and
Van Tuyl, Adam
2007.
The minimal resolutions of double points in P1×P1 with ACM support.
Journal of Pure and Applied Algebra,
Vol. 211,
Issue. 3,
p.
784.
Guardo, Elena
and
Van Tuyl, Adam
2008.
Separators of points in a multiprojective space.
manuscripta mathematica,
Vol. 126,
Issue. 1,
p.
99.
Bonacini, Paola
and
Marino, Lucia
2011.
On the Hilbert function of zero-dimensional schemes in $${{\mathbb P}^1 \times {\mathbb P}^1}$$.
Collectanea mathematica,
Vol. 62,
Issue. 1,
p.
57.
Guardo, Elena
and
Van Tuyl, Adam
2011.
Separators of fat points in Pn×Pm.
Journal of Pure and Applied Algebra,
Vol. 215,
Issue. 8,
p.
1990.
Guardo, Elena
and
Tuyl, Adam Van
2012.
Separators of arithmetically Cohen-Macaulay fat points ${\bf P}^1\times {\bf P}^1$.
Journal of Commutative Algebra,
Vol. 4,
Issue. 2,
Guardo, Elena
Harbourne, Brian
and
Van Tuyl, Adam
2013.
Fat lines in P3: Powers versus symbolic powers.
Journal of Algebra,
Vol. 390,
Issue. ,
p.
221.
Guardo, Elena
Harbourne, Brian
and
Van Tuyl, Adam
2013.
Symbolic Powers Versus Regular Powers of Ideals of General Points in ℙ1× ℙ1.
Canadian Journal of Mathematics,
Vol. 65,
Issue. 4,
p.
823.
Baczyńska, Magdalena
Dumnicki, Marcin
Habura, Agata
Malara, Grzegorz
Pokora, Piotr
Szemberg, Tomasz
Szpond, Justyna
and
Tutaj-Gasińska, Halszka
2014.
Points fattening on and symbolic powers of bi-homogeneous ideals.
Journal of Pure and Applied Algebra,
Vol. 218,
Issue. 8,
p.
1555.
Bonacini, Paola
and
Marino, Lucia
2015.
Hilbert functions and set of points in $${\varvec{\mathbb {P}}^{1}\times {\mathbb {P}}^{1}}$$ P 1 × P 1.
Beiträge zur Algebra und Geometrie / Contributions to Algebra and Geometry,
Vol. 56,
Issue. 1,
p.
43.
Guardo, Elena
and
Van Tuyl, Adam
2015.
Arithmetically Cohen-Macaulay Sets of Points in P^1 x P^1.
p.
71.
Brambilla, Maria Chiara
Dumitrescu, Olivia
and
Postinghel, Elisa
2016.
On linear systems of $$\mathbb {P}^3$$ P 3 with nine base points.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 195,
Issue. 5,
p.
1551.
Favacchio, Giuseppe
and
Guardo, Elena
2017.
The Minimal Free Resolution of Fat Almost Complete Intersections in ℙ1 × ℙ1.
Canadian Journal of Mathematics,
Vol. 69,
Issue. 6,
p.
1274.
Linh, Tran N. K.
Guardo, Elena
Le Ngoc, Long
Briš, R.
Chang, Gyu Whan
Khanh, Chu Duc
Razzaghi, M.
Stempak, K.
and
Phan, Thanh Toan
2018.
A Presentation of the Kähler Differential Module for a Fat Point Scheme in ℙn1 × … × ℙnk.
ITM Web of Conferences,
Vol. 20,
Issue. ,
p.
01007.
Favacchio, Giuseppe
Guardo, Elena
and
Migliore, Juan
2018.
On the arithmetically Cohen-Macaulay property for sets of points in multiprojective spaces.
Proceedings of the American Mathematical Society,
Vol. 146,
Issue. 7,
p.
2811.
Favacchio, Giuseppe
Guardo, Elena
and
Picone, Beatrice
2019.
Special arrangements of lines: Codimension 2 ACM varieties in ℙ1 × ℙ1 × ℙ1.
Journal of Algebra and Its Applications,
Vol. 18,
Issue. 04,
p.
1950073.
Carlini, Enrico
Catalisano, Maria Virginia
and
Oneto, Alessandro
2020.
On the Hilbert Function of General Fat Points in P 1 × P 1.
Michigan Mathematical Journal,
Vol. 69,
Issue. 3,
Gao, Jiyang
Li, Yutong
Loper, Michael C.
and
Mattoo, Amal
2021.
Virtual complete intersections in P1×P1.
Journal of Pure and Applied Algebra,
Vol. 225,
Issue. 1,
p.
106473.
Guardo, Elena
Kreuzer, Martin
Linh, Tran N. K.
and
Long, Le Ngoc
2021.
Kähler Differentials for Fat Point Schemes in ℙ1×ℙ1.
Journal of Commutative Algebra,
Vol. 13,
Issue. 2,
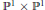 ${{\mathbb{P}}^{1\,}}\times \,{{\mathbb{P}}^{1}}$. If
${{\mathbb{P}}^{1\,}}\times \,{{\mathbb{P}}^{1}}$. If 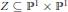 $Z\,\subseteq \,{{\mathbb{P}}^{1\,}}\times \,{{\mathbb{P}}^{1}}$ is an arbitrary fat point scheme, then it can be shown that for every
$Z\,\subseteq \,{{\mathbb{P}}^{1\,}}\times \,{{\mathbb{P}}^{1}}$ is an arbitrary fat point scheme, then it can be shown that for every 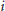 $i$ and
$i$ and 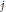 $j$ the values of the Hilbert function
$j$ the values of the Hilbert function 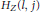 ${{H}_{Z}}(l,\,j)$ and
${{H}_{Z}}(l,\,j)$ and 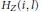 ${{H}_{Z}}(i,\,l)$ eventually become constant for
${{H}_{Z}}(i,\,l)$ eventually become constant for 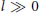 $l\,\gg \,0$. We show how to determine these eventual values by using only the multiplicities of the points, and the relative positions of the points in
$l\,\gg \,0$. We show how to determine these eventual values by using only the multiplicities of the points, and the relative positions of the points in 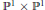 ${{\mathbb{P}}^{1\,}}\times \,{{\mathbb{P}}^{1}}$. This enables us to compute all but a finite number values of
${{\mathbb{P}}^{1\,}}\times \,{{\mathbb{P}}^{1}}$. This enables us to compute all but a finite number values of 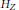 ${{H}_{Z}}$ without using the coordinates of points. We also characterize the
${{H}_{Z}}$ without using the coordinates of points. We also characterize the 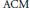 $\text{ACM}$ fat point schemes using our description of the eventual behaviour. In fact, in the case that
$\text{ACM}$ fat point schemes using our description of the eventual behaviour. In fact, in the case that 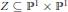 $Z\,\subseteq \,{{\mathbb{P}}^{1\,}}\times \,{{\mathbb{P}}^{1}}$ is
$Z\,\subseteq \,{{\mathbb{P}}^{1\,}}\times \,{{\mathbb{P}}^{1}}$ is 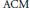 $\text{ACM}$, then the entire Hilbert function and its minimal free resolution depend solely on knowing the eventual values of the Hilbert function.
$\text{ACM}$, then the entire Hilbert function and its minimal free resolution depend solely on knowing the eventual values of the Hilbert function.

