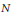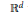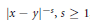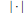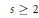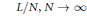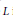1 results
Lower Order Terms of the Discrete Minimal Riesz Energy on Smooth Closed Curves
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 1 / 01 February 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 24-43
- Print publication:
- 01 February 2012
-
- Article
-
- You have access
- Export citation
-
We consider the problem of minimizing the energy of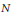
$N$ points repelling each other on curves in 
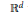${{\mathbb{R}}^{d}}$ with the potential 
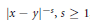${{\left| x\,-\,y \right|}^{-s}},\,s\,\ge \,1$, where 
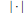$\left| \cdot \right|$ is the Euclidean norm. For a sufficiently smooth, simple, closed, regular curve, we find the next order term in the asymptotics of the minimal s-energy. On our way, we also prove that at least for 
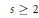$s\,\ge \,2$, the minimal pairwise distance in optimal configurations asymptotically equals 
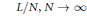$L/N,\,N\to \,\infty $, where 
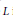$L$ is the length of the curve.
