Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T06:38:21.933Z Has data issue: false hasContentIssue false
  • English
  • Français

Lower Order Terms of the Discrete Minimal Riesz Energy on Smooth Closed Curves

Published online by Cambridge University Press:  20 November 2018

S. V. Borodachov
S. V. Borodachov*
Affiliation:
Department of Mathematics, Towson University, 8000 York Road, Towson, MD, 21252, USA email: sborodachov@towson.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the problem of minimizing the energy of 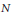$N$ points repelling each other on curves in 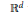${{\mathbb{R}}^{d}}$ with the potential 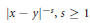${{\left| x\,-\,y \right|}^{-s}},\,s\,\ge \,1$, where 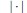$\left| \cdot \right|$ is the Euclidean norm. For a sufficiently smooth, simple, closed, regular curve, we find the next order term in the asymptotics of the minimal s-energy. On our way, we also prove that at least for 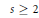$s\,\ge \,2$, the minimal pairwise distance in optimal configurations asymptotically equals 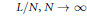$L/N,\,N\to \,\infty $, where 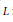$L$ is the length of the curve.

Keywords

31C2065D17minimal discrete Riesz energylower order termpower law potentialseparation radius
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 1 , 01 February 2012 , pp. 24 - 43
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Abrams, A., Cantarella, J., Fu, J. H. G., Ghomi, M., and Howard, R., Circles minimize most knot energies. Topology 42(2003), 381-394. http://dx. doi. org/10.1016/S0040-9383(02)00016-2Google Scholar
[2] Andreev, N. N., An extremal property of the icosahedron. East J. Approx. 2(1996), no. 4, 459-462.Google Scholar
[3] Andreev, N. N., Location of points on a sphere with minimal energy. (Russian) Tr. Mat. Inst. Steklova 219(1997), Teor. Priblizh. Garmon. Anal., 27-31.Google Scholar
[4] Berkenbusch, M. K., Claus, I., Dunn, C., Kadanoff, L. P., Nicewicz, M., and Venkataramani, S. C., Discrete charges on a two dimensional conductor. J. Statist. Phys. 116(2004), no. 5-6, 1301-1358. http://dx. doi. org/10.1023/B:JOSS.0000041741.27244. acGoogle Scholar
[5] Borodachov, S. V., Hardin, D. P., and Saff, E. B., Asymptotics for discrete weighted minimal Riesz energy problems on rectifiable sets. Trans. Amer. Math. Soc. 360(2008), no. 3, 1559-1580. http://dx. doi. org/10.1090/S0002-9947-07-04416-9Google Scholar
[6] Brauchart, J. S., About the second term of the asymptotics for optimal Riesz energy on the sphere in the potential-theoretical case. Integral Transforms Spec. Funct. 17(2006), no. 5, 321-328. http://dx. doi. org/10.1080/10652460500431859Google Scholar
[7] Brauchart, J. S., Optimal logarithmic energy points on the unit sphere. Math. Comp. 77(2008), no. 263, 1599-1613. http://dx. doi. org/10.1090/S0025-5718-08-02085-1Google Scholar
[8] Brauchart, J. S., Hardin, D. P., and Saff, E. B., Discrete energy asymptotics on a Riemannian circle. Unif. Distrib. Theory 6(2011), to appear.Google Scholar
[9] Brauchart, J. S., Hardin, D. P., and Saff, E. B., The Riesz energy of the N-th roots of unity: an asymptotic expansion for large N. Bull. Lond. Math. Soc. 41(2009), no. 4, 621-633. http://dx. doi. org/10.1112/blms/bdp034Google Scholar
[10] Brauchart, J. S., Hardin, D. P., and Saff, E. B., The support of the limit distribution of optimal Riesz energy points on sets of revolution in R3. J. Math. Phys. 48(2007), no. 12, 122901, 24 pp. http://dx. doi. org/10.1063/1.2817823Google Scholar
[11] Cohn, H. and Kumar, A., Universally optimal distribution of points on spheres. J. Amer. Math. Soc. 20(2007), no. 1, 99-148. http://dx. doi. org/10.1090/S0894-0347-06-00546-7Google Scholar
[12] Dahlberg, B. E. J., On the distribution of Fekete points. Duke Math. J. 45(1978), 537-542. http://dx. doi. org/10.1215/S0012-7094-78-04524-6Google Scholar
[13] Dragnev, P. D., Legg, D. A., and Townsend, D. W., Discrete logarithmic energy on the sphere. Pacific J. Math. 207(2002), no. 2, 345-358. http://dx. doi. org/10.2140/pjm.2002.207.345Google Scholar
[14] Dragnev, P. D. and Saff, E. B., Riesz spherical potentials with external fields and minimal energy points separation. Potential Anal. 26(2007), no. 2, 139-162. http://dx. doi. org/10.1007/s11118-006-9032-2Google Scholar
[15] Freedman, M. H., He, Z.-X., and Wang, Z., Möbius energy of knots and unknots. Ann. of Math. 139(1994), no. 1, 1-50. http://dx. doi. org/10.2307/2946626Google Scholar
[16] Götz, M. and Saff, E. B., Note on d-extremal configurations for the sphere in Rd+1. In: Recent progress in multivariate approximation (Witten-Bommerholz, 2000), Internat. Ser. Numer. Math., 137, Birkhäuser, Basel, 2001, pp. 159-162.Google Scholar
[17] Habicht, W. and van der Waerden, B. L., Lagerung von Punkten auf dem Kugel. Math. Ann. 123(1951), 223-234. http://dx. doi. org/10.1007/BF02054950Google Scholar
[18] Hardin, D. P. and Saff, E. B., Discretizing manifolds via minimum energy points. Notices Amer. Math. Soc. 51(2004), no. 10, 1186-1194.Google Scholar
[19] Hardin, D. P. and Saff, E. B., Minimal Riesz energy point configurations for rectifiable d-dimensional manifolds. Adv. Math. 193(2005), no. 1, 173-204. http://dx. doi. org/10.1016/j. aim.2004.05.006Google Scholar
[20] Hardin, D. P., Saff, E. B., and Stahl, H., Support of the logarithmic equilibrium measure on sets of revolution in R3. J. Math. Phys. 48(2007), no. 2, 022901, 14 pp. http://dx. doi. org/10.1063/1.2435084Google Scholar
[21] Kolushov, A. V. and Yudin, V. A., Extremal dispositions of points on the sphere. Anal. Math. 23(1997), no. 1, 25-34. http://dx. doi. org/10.1007/BF02789828Google Scholar
[22] Kolushov, A. V. and Yudin, V. A., On the Korkin-Zolotarev construction (Russian). Diskret. Mat. 6(1994), no. 1, 155-157.Google Scholar
[23] Korevaar, J. and Kortram, R. A., Equilibrium distributions of electrons on smooth plane conductors. Nederl. Akad. Wetensch. Indag. Math. 45(1983), no. 2, 203-219.Google Scholar
[24] Korevaar, J. and Monterie, M. A., Approximation of the equilibrium distribution by distributions of equal point charges with minimal energy. Trans. Amer. Math. Soc. 350(1998), no. 6, 2329-2348. http://dx. doi. org/10.1090/S0002-9947-98-02187-4Google Scholar
[25] Korevaar, J. and Monterie, M. A., Fekete potentials and polynomials for continua. J. Approx. Theory 109(2001), no. 1, 110-125. http://dx. doi. org/10.1006/jath.2000.3535Google Scholar
[26] Kuijlaars, A. B. J. and Saff, E. B., Asymptotics for minimal discrete energy on the sphere. Trans. Amer. Math. Soc. 350(1998), no. 2, 523-538. http://dx. doi. org/10.1090/S0002-9947-98-02119-9Google Scholar
[27] Kuijlaars, A. B. J., Saff, E. B., and Sun, X., On separation of minimal Riesz energy points on spheres in Euclidean spaces. J. Comput. Appl. Math. 199(2007), no. 1, 172-180. http://dx. doi. org/10.1016/j. cam.2005.04.074Google Scholar
[28] Landkof, N. S., Foundations of modern potential theory. Die Grundlehren der mathematischen Wissenschaften, 180, Springer-Verlag, New York-Heidelber, 1972.Google Scholar
[29] Martinez-Finkelstein, A., Maymeskul, V., Rakhmanov, E. A., and Saff, E. B., Asymptotics for minimal discrete Riesz energy on curves in Rd. Canad. J. Math. 56(2004), no. 3, 529-552. http://dx. doi. org/10.4153/CJM-2004-024-1Google Scholar
[30] O’Hara, J., Energy of a knot. Topology 30(1991), no. 2, 241-247. http://dx. doi. org/10.1016/0040-9383(91)90010-2Google Scholar
[31] O’Hara, J., Family of energy functionals of knots. Topology Appl. 48(1992), no. 2, 147-161. http://dx. doi. org/10.1016/0166-8641(92)90023-SGoogle Scholar
[32] O’Hara, J., Energy functionals of knots. II. Topology Appl. 56(1994), no. 1, 45-61. http://dx. doi. org/10.1016/0166-8641(94)90108-2Google Scholar
[33] Pommerenke, Ch., Über die Verteilung der Fekete-Punkte. II. (German) Math. Ann. 179(1969), 212-218. http://dx. doi. org/10.1007/BF01358488Google Scholar
[34] Szegö, G., Bemerkungen zu einer Arbeit von Herrn M. Fekete: Über die Verteilung der Wurzeln bei gewissen algebraischen Gleichungen mit ganzzahligen Koeffizienten. Mathematische Zeitschrift 21(1924), no. 1, 203-208. http://dx. doi. org/10.1007/BF01187465Google Scholar
[35] Thomson, J. J., On the structure of the atom: an investigation of the stability and periods of oscillation of a number of corpuscles arranged at equal intervals around the circumference of a circle; with application of the results to the theory of atomic structure. Philosophical Magazine (6) 7(1904), no. 39, 237-265.Google Scholar
[36] Yudin, V. A., The minimum of potential energy of a system of point charges. Discrete Math. Appl. 3(1993), no. 1, 75-81.Google Scholar