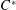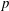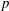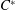Very recently, Karder and Petek completely described maps on density matrices (positive semidefinite matrices with unit trace) preserving certain entropy-like convex functionals of any convex combination. As a result, maps could be characterized that preserve von Neumann entropy or Schatten 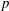 $p$-norm of any convex combination of quantum states (whose mathematical representatives are the density matrices). In this note we consider these latter two problems on the set of invertible density operators, in a much more general setting, on the set of positive invertible elements with unit trace in a
$p$-norm of any convex combination of quantum states (whose mathematical representatives are the density matrices). In this note we consider these latter two problems on the set of invertible density operators, in a much more general setting, on the set of positive invertible elements with unit trace in a 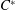 $C^{\ast }$-algebra.
$C^{\ast }$-algebra.
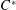 $C^{\ast }$-algebras Preserving von Neumann Entropy or Schatten
$C^{\ast }$-algebras Preserving von Neumann Entropy or Schatten 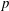 $p$-norm of Convex Combinations
$p$-norm of Convex Combinations