We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We find an upper bound for the number of groups of order n up to isomorphism in the variety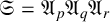 
${\mathfrak {S}}={\mathfrak {A}_p}{\mathfrak {A}_q}{\mathfrak {A}_r}$, where p, q and r are distinct primes. We also find a bound on the orders and on the number of conjugacy classes of subgroups that are maximal amongst the subgroups of the general linear group that are also in the variety 
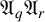$\mathfrak {A}_q\mathfrak {A}_r$.
