Let 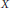 $X$ be a locally compact non-compact Hausdorff topological space. Consider the algebras
$X$ be a locally compact non-compact Hausdorff topological space. Consider the algebras 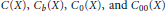 $C\left( X \right),{{C}_{b}}\left( X \right),{{C}_{0}}\left( X \right),\,\text{and}\,{{C}_{00}}\left( X \right)$ of respectively arbitrary, bounded, vanishing at infinity, and compactly supported continuous functions on
$C\left( X \right),{{C}_{b}}\left( X \right),{{C}_{0}}\left( X \right),\,\text{and}\,{{C}_{00}}\left( X \right)$ of respectively arbitrary, bounded, vanishing at infinity, and compactly supported continuous functions on 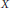 $X$. Of these, the second and third are
$X$. Of these, the second and third are 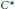 ${{C}^{*}}$-algebras, the fourth is a normed algebra, whereas the first is only a topological algebra (it is indeed a pro-
${{C}^{*}}$-algebras, the fourth is a normed algebra, whereas the first is only a topological algebra (it is indeed a pro-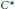 ${{C}^{*}}$- algebra). The interesting fact about these algebras is that if one of them is given, the others can be obtained using functional analysis tools. For instance, given the
${{C}^{*}}$- algebra). The interesting fact about these algebras is that if one of them is given, the others can be obtained using functional analysis tools. For instance, given the 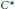 ${{C}^{*}}$-algebra
${{C}^{*}}$-algebra 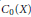 ${{C}_{0}}\left( X \right)$, one can get the other three algebras by
${{C}_{0}}\left( X \right)$, one can get the other three algebras by 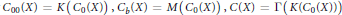 ${{C}_{00}}\left( X \right)=K\left( {{C}_{0}}\left( X \right) \right),{{C}_{b}}\left( X \right)=M\left( {{C}_{0}}\left( X \right) \right),C\left( X \right)=\Gamma \left( K\left( {{C}_{0}}\left( X \right) \right) \right)$, where the right hand sides are the Pedersen ideal, the multiplier algebra, and the unbounded multiplier algebra of the Pedersen ideal of
${{C}_{00}}\left( X \right)=K\left( {{C}_{0}}\left( X \right) \right),{{C}_{b}}\left( X \right)=M\left( {{C}_{0}}\left( X \right) \right),C\left( X \right)=\Gamma \left( K\left( {{C}_{0}}\left( X \right) \right) \right)$, where the right hand sides are the Pedersen ideal, the multiplier algebra, and the unbounded multiplier algebra of the Pedersen ideal of 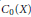 ${{C}_{0}}\left( X \right)$, respectively. In this article we consider the possibility of these transitions for general
${{C}_{0}}\left( X \right)$, respectively. In this article we consider the possibility of these transitions for general 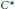 ${{C}^{*}}$-algebras. The difficult part is to start with a pro-
${{C}^{*}}$-algebras. The difficult part is to start with a pro-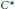 ${{C}^{*}}$-algebra A and to construct a
${{C}^{*}}$-algebra A and to construct a 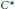 ${{C}^{*}}$-algebra
${{C}^{*}}$-algebra 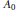 ${{A}_{0}}$ such that
${{A}_{0}}$ such that 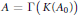 $A=\Gamma \left( K\left( {{A}_{0}} \right) \right)$. The pro-
$A=\Gamma \left( K\left( {{A}_{0}} \right) \right)$. The pro-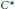 ${{C}^{*}}$-algebras for which this is possible are called locally compact and we have characterized them using a concept similar to that of an approximate identity.
${{C}^{*}}$-algebras for which this is possible are called locally compact and we have characterized them using a concept similar to that of an approximate identity.