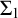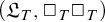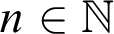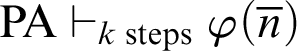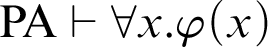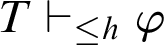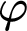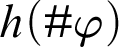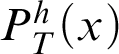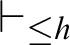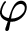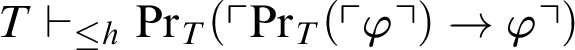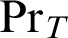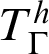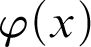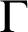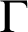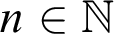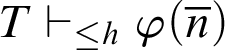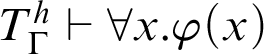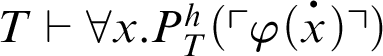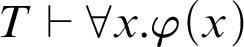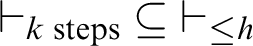We prove a strengthened version of Shavrukov’s result on the non-isomorphism of diagonalizable algebras of two $\Sigma _1$-sound theories, based on the improvements previously found by Adamsson. We then obtain several corollaries to the strengthened result by applying it to various pairs of theories and obtain new non-isomorphism examples. In particular, we show that there are no surjective homomorphisms from the algebra $(\mathfrak {L}_T, \Box _T\Box _T)$ onto the algebra $(\mathfrak {L}_T, \Box _T)$. The case of bimodal diagonalizable algebras is also considered. We give several examples of pairs of theories with isomorphic diagonalizable algebras but non-isomorphic bimodal diagonalizable algebras.

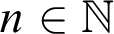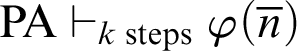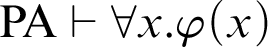Kreisel’s conjecture is the statement: if, for all $n\in \mathbb {N}$ , $\mathop {\text {PA}} \nolimits \vdash _{k \text { steps}} \varphi (\overline {n})$ , then $\mathop {\text {PA}} \nolimits \vdash \forall x.\varphi (x)$ . For a theory of arithmetic T, given a recursive function h, 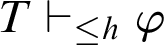$T \vdash _{\leq h} \varphi $ holds if there is a proof of 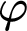$\varphi $ in T whose code is at most 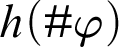$h(\#\varphi )$ . This notion depends on the underlying coding. 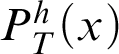${P}^h_T(x)$ is a predicate for 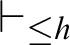$\vdash _{\leq h}$ in T. 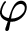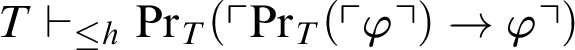It is shown that there exist a sentence $\varphi $ and a total recursive function h such that $T\vdash _{\leq h}\mathop {\text {Pr}} \nolimits _T(\ulcorner \mathop {\text {Pr}} \nolimits _T(\ulcorner \varphi \urcorner )\rightarrow \varphi \urcorner )$ , but 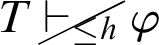, where 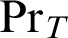$\mathop {\text {Pr}} \nolimits _T$ stands for the standard provability predicate in T. This statement is related to a conjecture by Montagna. Also variants and weakenings of Kreisel’s conjecture are studied. By the use of reflexion principles, one can obtain a theory 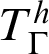$T^h_\Gamma $ that extends T such that a version of Kreisel’s conjecture holds: given a recursive function h and 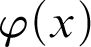$\varphi (x)$ a 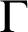$\Gamma $ -formula (where 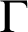$\Gamma $ is an arbitrarily fixed class of formulas) such that, for all 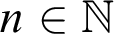$n\in \mathbb {N}$ , 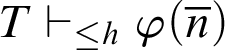$T\vdash _{\leq h} \varphi (\overline {n})$ , then 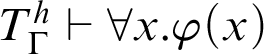$T^h_\Gamma \vdash \forall x.\varphi (x)$ . Derivability conditions are studied for a theory to satisfy the following implication: if 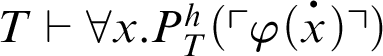, then 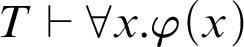$T\vdash \forall x.\varphi (x)$ . This corresponds to an arithmetization of Kreisel’s conjecture. 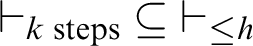It is shown that, for certain theories, there exists a function h such that $\vdash _{k \text { steps}}\ \subseteq\ \vdash _{\leq h}$ .