No CrossRef data available.
Article contents
ON SHAVRUKOV’S NON-ISOMORPHISM THEOREM FOR DIAGONALIZABLE ALGEBRAS
Published online by Cambridge University Press: 12 September 2022
Abstract
We prove a strengthened version of Shavrukov’s result on the non-isomorphism of diagonalizable algebras of two 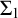 $\Sigma _1$-sound theories, based on the improvements previously found by Adamsson. We then obtain several corollaries to the strengthened result by applying it to various pairs of theories and obtain new non-isomorphism examples. In particular, we show that there are no surjective homomorphisms from the algebra
$\Sigma _1$-sound theories, based on the improvements previously found by Adamsson. We then obtain several corollaries to the strengthened result by applying it to various pairs of theories and obtain new non-isomorphism examples. In particular, we show that there are no surjective homomorphisms from the algebra 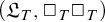 $(\mathfrak {L}_T, \Box _T\Box _T)$ onto the algebra
$(\mathfrak {L}_T, \Box _T\Box _T)$ onto the algebra 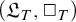 $(\mathfrak {L}_T, \Box _T)$. The case of bimodal diagonalizable algebras is also considered. We give several examples of pairs of theories with isomorphic diagonalizable algebras but non-isomorphic bimodal diagonalizable algebras.
$(\mathfrak {L}_T, \Box _T)$. The case of bimodal diagonalizable algebras is also considered. We give several examples of pairs of theories with isomorphic diagonalizable algebras but non-isomorphic bimodal diagonalizable algebras.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic


