1 results
Large Sets not Containing Images of a Given Sequence
-
- Journal:
- Canadian Mathematical Bulletin / Volume 26 / Issue 1 / 01 March 1983
- Published online by Cambridge University Press:
- 20 November 2018, pp. 41-43
- Print publication:
- 01 March 1983
-
- Article
-
- You have access
- Export citation
-
In the first part we construct a subset H of positive measure in the unit interval and a zero-sequence {an} so that H contains no homothetic copy of {an}. In Theorem 2 we prove that if ε > 0 and a zero-sequence {an} are given then there exists a set A of measure less than ε so that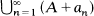
covers the interval. An application of this result is Theorem 3: for any sequence {an} and ε > 0 there is a set H of measure 1 - ε such that for no N and c is {an + c}n ≥ N contained by H.
covers the interval. An application of this result is Theorem 3: for any sequence {a