We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let X be a Banach space and 
. Let Π and Π0 be two subspaces of 
, the Banach space of bounded continuous functions from 𝕁 to X. We seek conditions under which Π + Π0 is closed in 
. This led to introduce a general 
space, which contains many classes of almost periodic type functions as subspaces. We prove some recent results on indefinite integral for the elements of these classes. We apply certain results on harmonic analysis to investigate solutions of differential equations. As an application we study specific 
spaces: the spaces of asymptotic and pseudo almost automorphic functions and their solutions of some ordinary quasi-linear and a non-linear parabolic partial differential equations.
Let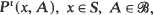 
t ≥ 0 be a Markov transition probability semigroup on a general space 
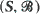satisfying a suitable φ-irreducibility condition. We show the existence of (i) a decay parameter λ ≥ 0 which is a common abscissa of convergence of the integrals ƒ estPt (x, A) dt for almost all x and all suitable A, (ii) a natural classification into λ-positive, λ-null and λ-transient cases. Moreover this classification is completely determined by any one of the h-skeleton chains of (Pt). We study the convergence of eλtPt(x, A) in the λ-positive case, and show that the limit f(X)π(A) (where f and π are the unique λ-invariant function and measure, normalized so that π(f) = 1) is reached at a uniform exponential rate of convergence, i.e. ||eλtPt(x, ·)-f(x)π(·)||f = O (e−αt) for some α > 0 and almost all x if there is a π-positive set such that the convergence is exponentially fast on this set. These results are used to deduce conditions for (Pt) to have quasi-stationary distributions.
Criteria are established for a discrete-time Markov process {Xn}n≧0 in Rd to have strictly positive, respectively zero, probability of escaping to infinity. These criteria are mainly in terms of the mean displacement vectors μ(y) = E{Xn+1|Xn = y} – y, and are essentially such that they force a deterministic process 
w.p.1 to move off to infinity, respectively to return to a compact set infinitely often. As an application we determine of most two-dimensional birth and death processes with rates linearly dependent on the population, whether they can escape to infinity or not.
