Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T11:57:03.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Exponential decay and ergodicity of general Markov processes and their discrete skeletons

Published online by Cambridge University Press:  01 July 2016

Pekka Tuominen  and
Richard L. Tweedie
Pekka Tuominen
Affiliation:
University of Western Australia
Richard L. Tweedie
Affiliation:
University of Western Australia
Get access Rights & Permissions [Opens in a new window]

Abstract

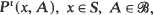Let t ≥ 0 be a Markov transition probability semigroup on a general space 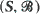satisfying a suitable φ-irreducibility condition. We show the existence of (i) a decay parameter λ ≥ 0 which is a common abscissa of convergence of the integrals ƒ estPt (x, A) dt for almost all x and all suitable A, (ii) a natural classification into λ-positive, λ-null and λ-transient cases. Moreover this classification is completely determined by any one of the h-skeleton chains of (Pt). We study the convergence of eλtPt(x, A) in the λ-positive case, and show that the limit f(X)π(A) (where f and π are the unique λ-invariant function and measure, normalized so that π(f) = 1) is reached at a uniform exponential rate of convergence, i.e. ||eλtPt(x, ·)-f(x)π(·)||f = O (e−αt) for some α > 0 and almost all x if there is a π-positive set such that the convergence is exponentially fast on this set. These results are used to deduce conditions for (Pt) to have quasi-stationary distributions.

Keywords

IRREDUCIBLERECURRENTINVARIANT MEASURESTATIONARY MEASUREQUASI-STATIONARY DISTRIBUTIONGEOMETRIC ERGODICITY
Type
Research Article
Information
Advances in Applied Probability , Volume 11 , Issue 4 , December 1979 , pp. 784 - 803
Copyright
Copyright © Applied Probability Trust 1979 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Arjas, E., Nummelin, E. and Tweedie, R. L. (1979) Semi-Markov processes on a general state space: α-theory and quasi-stationarity. Submitted for publication.Google Scholar
2. Azéma, J., Kaplan-Duflo, M. and Revuz, D. (1967) Mesure invariante sur les classes récurrentes des processus de Markov. Z. Wahrscheinlichkeitsth. 8, 157–181.Google Scholar
3. Blumenthal, R. M. and Getoor, R. K. (1968) Markov Processes and Potential Theory. Academic Press, New York.Google Scholar
4. Kendall, D. G. (1955) Some analytical properties of continuous stationary Markov transition functions. Trans. Amer. Math. Soc. 78, 529–540.CrossRefGoogle Scholar
5. Kingman, J. F. C. (1963) The exponential decay of Markov transition probabilities. Proc. London Math. Soc. (3) 13, 337–358.CrossRefGoogle Scholar
6. Kingman, J. F. C. (1963) Ergodic properties of continuous-time Markov processes and their discrete skeletons. Proc. London Math. Soc. (3) 13, 593–604.Google Scholar
7. Nummelin, E. (1976) A splitting technique for φ-recurrent Markov chains. Report HTTK-MAT A 80, Helsinki University of Technology.Google Scholar
8. Nummelin, E. (1976) Limit theorems for α-recurrent Markov processes. Adv. Appl. Prob. 8, 531–547.CrossRefGoogle Scholar
9. Nummelin, E. (1978) The discrete skeleton method and a total variation limit theorem for continuous-time Markov processes. Math. Scand. 42, 150–160.CrossRefGoogle Scholar
10. Nummelin, E. and Tweedie, R. L. (1978) Geometric ergodicity and R-positivity for general Markov chains. Ann. Prob. 6, 404–420.CrossRefGoogle Scholar
11. Orey, S. (1971) Lecture Notes on Limit Theorems for Markov Chain Transition Probabilities. Van Nostrand Reinhold, London.Google Scholar
12. Pakes, A. G. (1974) Some limit theorems for Markov chains with applications to branching processes. In Studies in Probability and Statistics, ed. Williams, E. J., Jerusalem Academic Press.Google Scholar
13. Pollard, D. B. and Tweedie, R. L. (1975) R-theory for Markov chains on a topological state space I. J. London Math. Soc. 10, 389–400.CrossRefGoogle Scholar
14. Seneta, E. and Vere-Jones, D. (1966) On quasi-stationary distributions in discrete-time Markov chains with a denumerable infinity of states. J. Appl. Prob. 3, 403–434.CrossRefGoogle Scholar
15. Tuominen, P. and Tweedie, R. L. (1979) The recurrence structure of general Markov processes. Proc. London Math. Soc. (3) 38, 89–114.Google Scholar
16. Tuominen, P. and Tweedie, R. L. (1979) Exponential ergodicity in Markovian queueing and dam models. J. Appl. Prob. 16, (4).Google Scholar
17. Tweedie, R. L. (1974) R-theory for Markov chains on a general state space I: solidarity properties and R-recurrent chains. Ann. Prob. 2, 840–864.Google Scholar
18. Tweedie, R. L. (1974) Quasi-stationary distributions for Markov chains on a general state space. J. Appl. Prob. 11, 726–741.Google Scholar
19. Widder, D. V. (1946) The Laplace Transform. Princeton University Press, Princeton, N.J.Google Scholar
20. Winkler, W. (1978) Continuous parameter Markov processes. Ann. Prob. 6, 459–468.Google Scholar