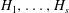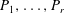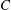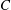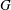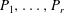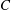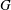Refine search
Actions for selected content:
2 results
Finiteness properties of cubulated groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 3 / March 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 453-506
- Print publication:
- March 2014
-
- Article
- Export citation
Classifying Spaces and Boundaries for Relatively Hyperbolic Groups
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 86 / Issue 3 / May 2003
- Published online by Cambridge University Press:
- 09 June 2003, pp. 666-684
- Print publication:
- May 2003
-
- Article
- Export citation