We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let T be the regular tree in which every vertex has exactly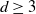 
$d\ge 3$
neighbours. Run a branching random walk on T, in which at each time step every particle gives birth to a random number of children with mean d and finite variance, and each of these children moves independently to a uniformly chosen neighbour of its parent. We show that, starting with one particle at some vertex 0 and conditionally on survival of the process, the time it takes for every vertex within distance r of 0 to be hit by a particle of the branching random walk is 
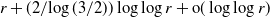$r + ({2}/{\log(3/2)})\log\log r + {\mathrm{o}}(\log\log r)$
.
