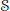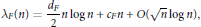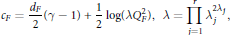A class of games for finding a leader among a group of candidates is studied in detail. This class covers games based on coin tossing and rock-paper-scissors as special cases and its complexity exhibits similar stochastic behaviors: either of logarithmic mean and bounded variance or of exponential mean and exponential variance. Many applications are also discussed.

In this paper, we apply the saddle-point method in conjunction with the theory of the Nörlund–Rice integrals to derive precise asymptotic formula for the generalized Li coefficients established by Omar and Mazhouda. Actually, for any function $F$ in the Selberg class 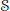$\mathcal{S}$ and under the Generalized Riemann Hypothesis, we have

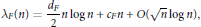$${{\lambda }_{F}}(n)\,=\,\frac{{{d}_{F}}}{2}n\,\log \,n\,+\,{{c}_{F}}n\,+\,O(\sqrt{n}\,\log \,n),$$

with

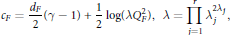$${{c}_{F}}\,=\,\frac{{{d}_{F}}}{2}(\gamma \,-\,1)\,+\,\frac{1}{2}\log (\lambda \text{Q}_{F}^{2}),\,\,\lambda \,=\,\prod\limits_{j=1}^{r}{\lambda _{j}^{2{{\lambda }_{j}}}},$$

where $\gamma $ is the Euler's constant and the notation is as below.

Let $\{d_j(n)\}_{j=1}^{\tau(n)}$ denote the increasing sequence of divisors of an integer $n$, and write $\Lambda_k(d)$ for the natural density of the set of those integers $n$ with $d_k(n)=d$. Answering a question raised by Erd\H os, we show that $\Lambda_k(d)$ attains its maximum for $d=K^{1/2+o(1)}$, where $K:=k^{(\log \log k)/\log 2}$ (which, by a theorem of Ramanujan, is roughly the size of the smallest integer having $k$ divisors). A key step of the proof consists in establishing a sublinearity property of the counting function $\Psi_1(x,y)$ of $y$-friable square-free integers not exceeding $x$. This is achieved via a complete study of $\Psi_1(x,y)$ using the saddle-point method, which, in particular, also enables a precise description of the Gaussian behaviour of this function in certain ranges.

2000 Mathematical Subject Classification: 11N25, 11N37.